Электрическое поле заряженного цилиндра

Заряженное тело в форме бесконечно длинного цилиндра с радиусом R, расположенное в диэлектрической среде с относительной диэлектрической проницаемостью ε₂ для двух случаев:

1. заряд равномерно распределен по объему цилиндра с линейной плотностью заряда ρ (Кл/м),

2. заряд находится только на поверхности цилиндра.

К первому случаю может относиться только диэлектрический цилиндр с относительной диэлектрической проницаемостью ε₁. Ко второму случаю относятся заряженные металлические сплошные и полые цилиндры.

Надо отдельно рассматривать поля внутри заряженного тела и вне его. При рассмотрении мы исходим из осевой симметрии этой задачи. Мы предполагаем, что величина вектора D зависит только от расстояния r от оси цилиндра, а его направление всегда совпадает с нормалью к оси цилиндра. Для решения задачи выбираем цилиндрическую форму поверхности с длиной l, радиусом r и осью, совпадающей с осью цилиндра.

Если r < R, то заряд внутри поверхности с радиусом r составит

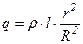для равномерно заряженного цилиндра и q=0 для шара с поверхностным зарядом.

Запишем выражение для теоремы Гаусса, учитывая, что поток вектора D через боковые поверхности равен 0, а поток вектора через боковую поверхность будет равен произведению D на площадь боковой поверхности цилиндра длиной l.

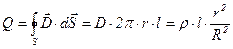. (13)

Для равномерно заряженного цилиндра, при получим для D и E

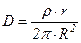, (14)

.

Для определения изменений потенциала мы можем воспользоваться выражением (6). Пользуясь тем, что интеграл в этом выражении не зависит от выбранного пути интегрировании, и, приняв потенциал на оси цилиндра за 0, для изменений потенциала получим

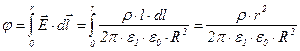
При , выражение (13) примет вид

. (15)

Тогда для D и Е будет справедливо

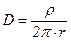, (16)

.

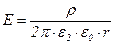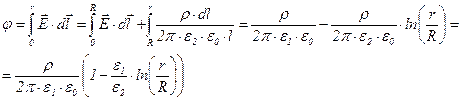
Выражения (14) и (16) для r=R дают одно и тоже значение D. Однако зависимость Е(r) в точке r=R имеет скачкообразное изменение (разрыв).

Для цилиндра с заряженной поверхностью, при справедливо

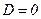и .

При будут справедливы выражения (16).

Рис.4

Date: 2015-05-18; view: 1934; Нарушение авторских прав