Приложение. В дифференциальной геометрии 1-форма определяется как линейная вещественная функция векторов, то есть является линейным оператором

В дифференциальной геометрии 1-форма определяется как линейная вещественная функция векторов, то есть является линейным оператором, «машиной», на вход которой подаются векторы, а на выходе получаются числа. Простейшей 1-формой является градиент d f функции f (обозначение d или grad обычно используют применительно к скалярным величинам, а Ñ (читай: «набла») – к векторам или тензорам). Внешняя производная, или градиент, является более строгой формой понятия «дифференциал». В отличие от дифференциала df, который выражает изменение f в некотором произвольном направлении, градиент характеризует изменение функции в определенном направлении, заданном бесконечно малым вектором смещения v. Если быть более точным, градиент d f представляет собой совокупность поверхностей уровня f ^a = const и характеризует их «близость» друг к другу, плотность «упаковки» в элементарном объеме в направлении v, с точностью до приближения их плоскостями и размещения через равные промежутки (вследствие линейности оператора). Результатом пересечения d f вектором смещения v является число á d f, v ñ = ¶ _v f. Это выражение определяет связь между градиентом d f и производной по направлению ¶ _v f. Введя вектор v в линейную машину d f, на выходе мы получаем ¶ _v f – число пересеченных плоскостей при прохождении v через d f, число, которое придостаточно малом v равно приращению f между основанием и острием вектора v.

Задание 1-формы в данной точке (связь с точечным описанием) для некоторого геометрического объекта, описывающего физическую величину, например, для тензора произвольного ранга (0-ранг – скаляр, 1-ранг – вектор или 1-форма, 2-ранг – тензор второго ранга и т. д.), предполагает выполнение трех основных операций. Это, прежде всего, задание вектора смещения, в направлении которого данный объект меняется от точки к точке. Во-вторых: моделирование исходного объекта в окрестностях каждой точки в виде плоских поверхностей уровня, расположенных на одинаковых расстояниях. И наконец, подсчет числа пересечений этих плоскостей вектором смещения. Поскольку образование 1-формы (градиента) от произвольного тензора предполагает одновременное задание вектора смещения, появляется дополнительный входной канал, и ранг исходного тензора увеличивается на единицу.

Таким образом, дифференциальная геометрия дает более строгое определение градиента в качестве 1-формы, в отличие от обычных представлений градиента как вектора. Градиент, который нам более знаком, – это всего лишь вектор, поставленный в соответствие 1-форме градиента с помощью уравнения (которое уже приводилось) 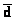f · v = á d f, v ñ, где слева стоит скалярное произведение двух векторов, и 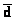f – градиент в виде вектора.

Дифференциальная геометрия расширяет также понятие тензора. Если обычно под тензором понимается линейный оператор с входными каналами для векторов и выходными данными либо в виде вещественных чисел, либо в виде векторов, то теперь во входной канал может подаваться не только вектор, но и 1-форма.

В качестве примера рассмотрим координатное представление тензора второго ранга. В отличие от обычного вектора, который может быть разложен лишь в одном произвольном базисе из ортонормированных векторов (поэтому его можно считать тензором первого ранга), тензор второго ранга разлагается на компоненты в двух базисах. В качестве любого из этих базисов (или обоих сразу) могут служить либо наборы из обычных базисных векторов e _a, либо совокупность так называемых базисных 1-форм w ^a = d x ^a. Базисные 1-формы – это координатные поверхности x ^a = const. Следовательно, базисный вектор e _aпересекает только одну поверхность базисной 1-формы w ^a (перпендикулярную e _a).

Точно так же, как произвольный вектор можно разложить по базису e _a, v = v ^a e _a, произвольную 1-форму можно разложить по базису w ^b, s = s_b w ^b. Коэффициенты v ^a и s_b называются компонентами вектора v и 1-формы s в базисе e _a и w ^b соответственно.

Вводя в некоторый тензор второго ранга S произвольные вектор v и 1-форму s и, зная компоненты их разложения в своих базисах, через них можно выразить компоненты самого тензора S (v, s) = S (e _a, w ^b) v ^as_b = S _a^b v ^as_b.

Date: 2015-05-18; view: 393; Нарушение авторских прав