Мета – анализ

В 1989 физиолог Диана Феррари и я, тогда работавший в Принстонском университете, применили мета-анализ, чтобы оценить доказательства для взаимодействия мысли с материей при игре в кости [148].

Как в любом мета-анализе, надо было включить каждое исследование, каждый поставленный эксперимент, которые возможно было найти; иначе можно было бы из-за личных предубеждений выбрать «хорошие» эксперименты и выбросить «плохие». Мы проверили все англоязычные журналы до 1989 г. в которых были опубликованы эксперименты по игре в кости и для каждого исследования записали чило участников,

сумму очков, которую надо было выбросить, общее число выбрасываемых костей и так далее. Из этой информации мы вычислили 50% случайную норму набираемой суммы. Кроме того, для каждого исследования мы отмечали присутствие или отсутствие определенных критериев, по которым оценивали качество эксперимента, причем общее число критериев было равно 13.

Наш литературный поиск дал 73 публикации, которые обобщили результаты работ 52 ученых с 1935 г. по 1987 г. В экспериментах участвовало 2569 человека, сделавших 2,6 миллиона бросков костей в 148 опытах с попыткой мысленного влияния. Было проведено также 150 000 контрольных бросков в 31 опыте, в которых не было никакого мысленного влияния. Общее количество бросков в одном опыте изменялось в пределах от 60 до 240 000; число участников менялось в пределах от 1 до 393.

На рис. 8.1 суммированы результаты этих экспериментов. Величина случайного ожидания (или случайный рейтинг) для опытов, в которых не было никакого мысленного влияния равен 50.02%. Но величина рейтинга для всех экспериментов с мысленным влиянием оказалась близка к 51.2%. На первый взгляд эта цифра не очень велика, но она означает, что можно поставить миллиард шансов против одного, что такая величина не обусловлена случайностью. Другими словами, миллиард шансов против одного, что существует эффект мысленного влияния на результаты экспериментов.

ответ критикам

Как мы видели раньше, основная критика объединенных экспериментальных результатов сводится к тому, что только ограниченное число исследователей опубликовали свои результаты полностью. Для экспериментов по игре игры в кости, число опытов на одного исследователя изменяется в пределах от 1 до 21, причем большинство ученых (64%) сообщили об одном, двух или трех опытах. Чтобы проверить критику, мы вычислили рейтинг опытов для тех 25 исследователей, которые сообщили только о трех или меньшем числе опытов. Результат остался высоко существенным, с отношением шансов миллиард к одному в пользу неслучайности явления. Поэтому нельзя думать, что положительный

результат обусловлен какими-то отдельными исследованиями.

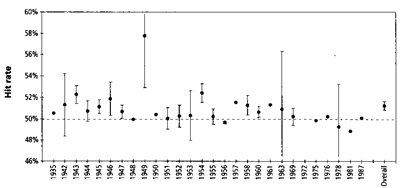Рис. 8.1. Величина рейтинга для всех экспериментов по годам с 50% величиной случайного рейтинга и 95% доверительным интервалом. Для тех лет, в которые проведены одиночные опыты доверительный интервал не показан. Общая оценка всех опытов с 95% доверительным интервалом показана в правом конце диаграммы.

Но могла быть такая ситуация, что завышение результатов всех экспериментов происходит вследствие искажения результатов отдельных экспериментов. Чтобы проверить такую возможность, мы удалили отдельные выдающиеся результаты таким же способом, как это сделали Хонортон и Феррари при мета-анализе опытов по предвидению. В нашем анализе, пришлось удалить 52 исследования (или 35% от общего количества), чтобы оставшиеся результаты были более однородными. В главе 4 обсуждалось, что в физических науках приходится исключать 45% данных, чтобы добиться однородности результатов. Общий эффект (в 96 остающихся опытах) после такого исключения остался статистически значимым, с величиной отношения шансов три миллиона к одному в пользу неслучайности явления. Таким образом, тот же самый эффект наблюдается и в остальных 96 опытах.

А если публикуются только удачные эксперименты?

Чтобы оценить эффект «черного ящика», мы попытались вычислить общее число неопубликованных, неудачных экспериментов, которые необходимы для того, чтобы заметно (до 20 к 1) уменьшить отношение шансов в пользу неслучайности явления. Оказалось, что общее число таких опытов дожно быть примерно 17974, или на одно опубликованное исследование должно приходится 121 неопубликованная работа, чтобы аннулировать установленный эффект. Иначе говоря, каждый из 52 исследователей должен был делать один неудачный эксперимент в месяц на протяжении 28 лет и его не публиковать. Такое предположение выходит за рамки разумных, поэтому нельзя объяснять результаты этих экспериментов выборочными, специально подобранными сообщениями.

Date: 2015-05-18; view: 555; Нарушение авторских прав