Собственные волновые функции квантового гармонического осциллятора

Полиномы Чебышева – Эрмита и их свойства

Перейдем к анализу волновых функций квантового гармонического осциллятора. Как показано в теории дифференциальных уравнений с переменными коэффициентами, волновые функции, являющиеся решениями уравнения (12), имеют вид

где 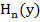- полином Чебышева-Эрмита n – го порядка, определяемый выражением

Отметим, что для этих полиномов справедливо рекуррентное соотношение

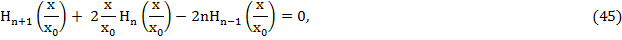
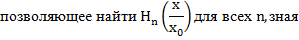
и

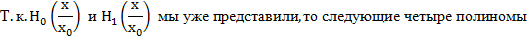
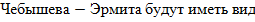
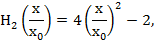
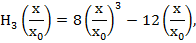
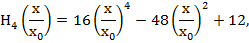
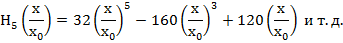
Волновые функции (43) ортонормированы, т.е. удовлетворяют условию:

где 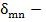символ Кронекера.

Приведем вид волновых функций для первых шести энергетических уровней квантового гармонического осциллятора

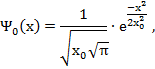
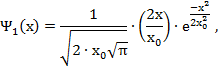
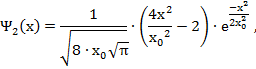
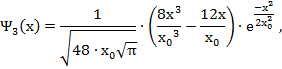
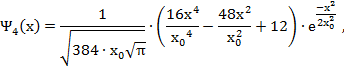
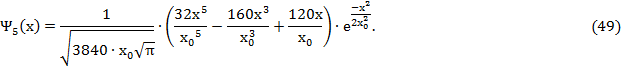
Графики волновых функций (49) для значений квантового числа n от 0 до 5 представлены на рисунке 4.

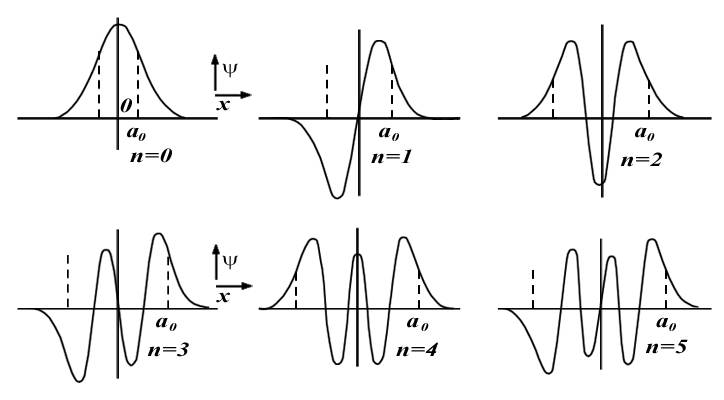
Рисунок 4 – Графики волновых функций квантового гармонического осциллятора

Отрезок 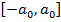определяет область, в которой совершал бы колебания классический осциллятор. Ширина этой области оказывается различной для разных значений квантового числа n, поскольку энергия осциллятора (32), а, следовательно, и амплитуда его колебаний (37) также зависят от n.

Из (43) – (49) следует, что волновые функции гармонического осциллятора обладают определенной четностью. Они являются четными функциями координаты x при четных значениях n и при , и нечетными функциями при нечетных n. Значение квантового числа n определяет также число точек пересечения волновой функции с осью x. В основном состоянии, т.е. при , точки пересечения внутри параболической ямы отсутствуют, при 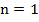имеется одна точка пересечения, при 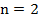- две и так далее.

Таким образом, при увеличении квантового числа n на единицу волновая функция гармонического осциллятора меняет четность и приобретает добавочную точку пересечения с осью x.

Отметим, что вне классической области 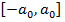волновые функции 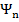отличны от нуля, что свидетельствует о том, что квантовый гармонический осциллятор с определенной вероятностью может находиться вне пределов параболической потенциальной ямы.

Из свойств полиномов Чебышева-Эрмита следует, что все их корни некратные и вещественные. Число корней полинома равно его степени n, в чем легко убедиться, анализируя приведенные выше выражения для полиномов низших степеней. На рисунке 5 приведены распределения плотности вероятности

для основного состояния квантового гармонического осциллятора (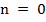) и для двух возбужденных состояний ().

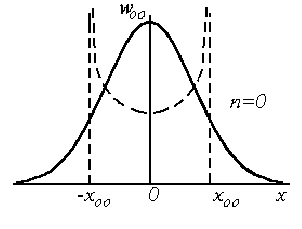
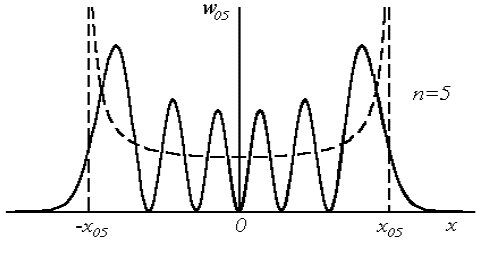
Рисунок 5 – Распределение плотности вероятности для трех состояний квантового гармонического осциллятора

На этом же рисунке показаны штриховыми кривыми вероятности найти частицу в окрестности точки x для классического осциллятора, совершающего гармонические колебания с теми же значениями полной энергии Е. Вертикальные штриховые линии соответствуют точкам поворота классического осциллятора ± x₀₀, ± x₀₁, ± x₀₅, и т.д. Эта вероятность, очевидно, пропорциональна его скорости, т.е. обратной величине квадратного корня из кинетической энергии. Следовательно, для классического осциллятора

где Е и U - полная и потенциальная энергия соответственно.

Отсюда видно, что вблизи точек поворота 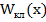стремится к бесконечности. Вблизи положения равновесия скорость осциллятора максимальна и соответственно классическая вероятность минимальна.

При малых n, что соответствует низшим энергетическим состояниям, квантовый и классический осцилляторы существенно ведут себя по разному. Однако, при достаточно больших энергиях функция (50) приближается к классической функции распределения как к некоторой средней величине, относительно которой она совершает быстрые осцилляции.

Отметим еще одну особенность квантово-механического осциллятора. Как видно из рисунка 5, вероятность обнаружить микрочастицу, совершающую квантово-механические колебания вне пределов, ограничивающих движение классического осциллятора, не равна нулю. Такое поведение квантово-механического осциллятора связано с более общим свойством микрочастиц проникать за пределы потенциальных барьеров, недоступных с точки зрения классической физики.

Заключение

В заключении, мы можем выделить ряд характерных для квантового гармонического осциллятора свойств:

1. Энергетический спектр частицы, находящейся в яме, является дискретным, т.е. энергия частицы квантуется.

2. Энергетические уровни квантового гармонического осциллятора являются эквидистантными, т.е. расположены на одинаковом энергетическом расстоянии друг от друга.

3. Частица, находящаяся в основном состоянии, т.е. на самом низшем энергетическом уровне, обладает не равной нулю энергией.

4. Плотность вероятности нахождения частицы (51) имеет максимумы в области между классическими точками поворота и экспоненциально спадает вне классической области. Это означает, что с определенной вероятностью частица может находиться вне ямы (за исключением ям с бесконечно высокими, непроницаемыми, стенками).

5. При увеличении квантового числа n на единицу волновая функция, описывающая поведение частицы в яме, приобретает дополнительную точку пересечения с осью x.

Следует отметить еще одно важное обстоятельство: энергетический спектр частицы является дискретным (энергия квантуется) только в тех случаях, когда частица находится в потенциальной яме. Если же частица движется в области потенциального порога, барьера, или над потенциальной ямой (при E 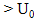), то ее энергетический спектр является непрерывным (квантование отсутствует). Этот результат согласуется с общей теоремой квантовой механики, согласно которой энергия всегда квантуется у систем, которые не могут уходить на бесконечность, и не квантуется у систем, способных уходить на бесконечность.

Отметим, что модель гармонического осциллятора и связанная с ним задача о движении частицы в параболической потенциальной яме является идеализацией, справедливой лишь при малых отклонениях колеблющейся частицы от положения равновесия. Во всех реальных ситуациях потенциальная энергия 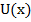частицы, совершающей колебания около положения равновесия, имеет более сложный по сравнению с (9) и (10) вид. Поэтому при возрастании амплитуды колебаний, начиная с некоторых значений амплитуд, движение частицы будет все больше отличаться от гармонических колебаний. Такое движение называют ангармоническим движением, а соответствующий осциллятор - ангармоническим осциллятором. Однако в случае малых колебаний влияние ангармонизма ничтожно мало, что позволяет использовать модель гармонического осциллятора для описания колебательного движения квантово-механических систем.

Date: 2015-05-18; view: 2047; Нарушение авторских прав