Собственные значения энергии квантового гармонического осциллятора

Уравнение (12) решаем методом разложения в ряд с предварительным выделением множителя, быстро убывающего на больших расстояниях от начала координат. Обозначим посредством Φ_∞ волновую функцию при больших значениях аргумента. Ей соответствует асимптотическая форма уравнения Шредингера

Решение уравнения (13) мы найдем из следующего соотношения

Подстановка этого решения (14) в (13) приводит к уравнению для ƒ(ξ):

Решение этого уравнения (15) будем искать в виде степенной функции

и подстановка ƒ(ξ) (выражение 16) в уравнение (13) дает

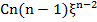
Второе слагаемое много больше первого, если n > 1 и ξ >> 1 (т.е. 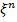>> 1). Поэтому первым слагаемым можно пренебречь. Приравнивая показатели степени ξ у второго и третьего членов, найдем

Таким образом, мы получили

Первое слагаемое физически бессмысленно, т.к. при любых ξ (т.е. x) функция 𝛹(x) < 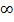ограничена, и асимптотическое поведение (ξ 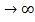) функции Φ(ξ) описывается вторым слагаемым в этом выражении.

Полное решение Φ(ξ) будем искать в виде

где F(ξ) – неизвестная функция. Постановка этого решения в уравнение (12) дает уравнение для F(ξ):

Уравнение (22) содержит во втором члене аргумент ξ в качестве сомножителя при производной. Поэтому оно принципиально отличается от линейных дифференциальных уравнений, описывающих поведение классического осциллятора. Будем искать его решение в виде ряда

где

Подставив F(ξ) из (23) в (22) и приравнивая коэффициенты при ξ одинаковых степенях, получим

,

,

,

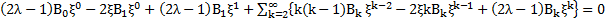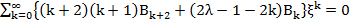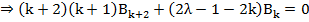откуда получаем рекуррентную формулу для коэффициентов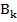

Отсюда следует, что все коэффициенты ряда (23) определены через две константы :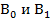

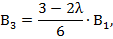
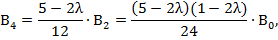
Таким образом, коэффициенты 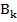образуют два независимых ряда, каждый из которых определяется через свою константу 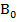или .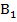

Найдем условие того, что функция (21) ограничена при любых ξ. Коэффициенты ряда, как только что выяснилось, убывают номером k, причем отношение

Такое поведение коэффициентов 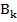еще не означает, что сумма ряда (23) конечна. Действительно, представив экспоненту 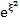в виде ряда

найдем

Сравнивая ряды (26) и (23), видим, что они имеют одинаковый вид, если 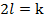(ряд (26) – разложение по 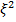). А тогда из (27) и (25) следует, что соотношение у коэффициентов ряда (26) при больших l то же, что и у коэффициентов ряда (23), т.е.

и, соответственно, функция (23) имеет асимптотику в виде экспоненты от :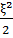

т.е. эта функция неограниченно возрастает при 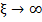. Поэтому единственный выход – оборвать ряд (23) на некотором 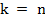, потребовав

Тогда λ примет следующие значения

Отсюда, с учетом введенного выше обозначения (10), находим возможные значения энергии квантового осциллятора:

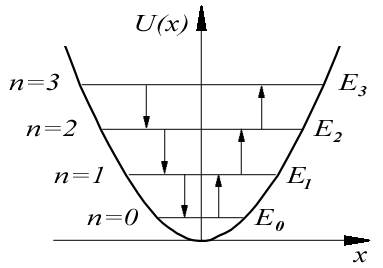
Это соотношение и определяет закон квантования энергии гармонического осциллятора. Отметим, что энергетические уровни гармонического осциллятора, в отличие, например, от случая прямоугольной потенциальной ямы, являются эквидистантными, т.е. расположены на одинаковом энергетическом расстоянии друг от друга (рисунок 3):

Рисунок 3 – Схема энергетических уровней квантового гармонического осциллятора

Date: 2015-05-18; view: 642; Нарушение авторских прав