Волновая функция и ее физический смысл. Уравнение Шредингера

Классическая механика позволяет точно определить положение импульса и энергию макроскопического тела, а также изменение этих величин под действием внешних сил. Квантовая механика учитывает соотношение неопределенности; ставит задачу: найти вероятность состояния частицы, т.е.вероятность ее координаты, импульса и энергии внутри некоторого элементарного объема или в течении некоторого элементарного промежутка времени. Классич. дифференц. ур-ию 2-ого порядка (2 закон Ньютона: 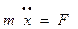) 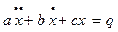. Квантовая механика составляет дифференциальное уравнение 2 порядка в частных производных (переменными являются координата и время) сформулированное в 1926 немецким физиком Шредингером: 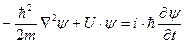(1) – нестационарное уравнение Шредингера. 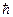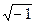- постоянная Планка, m – масса частицы, - волновая функция, i= - мнимая единица, 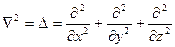- оператор Лапласа, U – функция координат и времени. Уравнение Шредингера является основным уравнением нерелятивистской квантовой механики. В одномерном случае решением данного уравнения является уравнение вида: 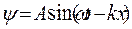- тригонометрическое или 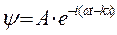- экспоненциальное которое представляет собой плоскую волну де Бройля с длиной волны . В данное выражение входит некоторая комплексная функция является функцией координат и времени которая называется волновой функцией или -функция. Физический смысл имеет не сама волновая функция, а произведение волновой функции на сопряженную с ней комплексную функцию *: *=| |² которая является плотностью вероятности нахождения частицы в данном элементарном объеме dV: 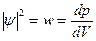т.е. 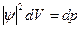определяет вероятность нахождения частицы в данном элементе объема 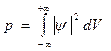. Для реально существующей частицы должно выполнятся так называемое условие нормировки функции, т.е. . На -функцию накладываются ограничения: 1) релятивистское движение не рассматривается, так что m=const. 2) непрерывна, однозначна и имеет непрерывную производную. 3) 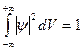имеет конечное значение. Смысл заключается в том, что интеграл пропорционален вероятности нахождения частицы в данном объеме. Из физического смысла -функции вытекает, что квантовая механика имеет статистически вероятностный характер. Она не позволяет определить точное местоположение частицы в пространстве или ее траекторию по которой она движется. -функция позволяет лишь предсказать с какой вероятностью частица может находиться в той или иной точке пространства. Если силовое поле U в которой движется частица стационарно, то данная функция U не зависит от времени и будет иметь смысл потенциальной энергии. В этом случае -функция распадается на 2 множителя (x,y,z.t)= 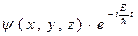(2), где E=U+K – полная энергия частицы. Возьмем производную по пространственной координате и времени (2) и подставим в (1), то получим (3): - стационарное уравнение Шредингера. 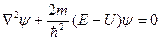(4), где m – масса частицы, E – полная энергия, U – потенциальная энергия. Уравнение (3) можно встретить в ви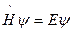де: , где 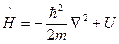- оператор Гамильтона. Учитывая, что 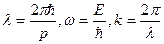перепишем выражение для волновой функции в экспоненциальном виде 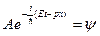. Дифференцируя данное выражение по координате х, а затем по времени t, получим 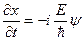. Следует, что полная энергия 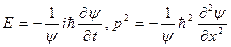. Окончательное решение уравнения Шредингера в стационарном виде является плоская волновая функция вида: 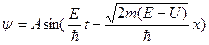- тригонометрический вид

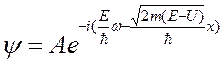- экспоненциальный вид

Date: 2015-05-18; view: 863; Нарушение авторских прав