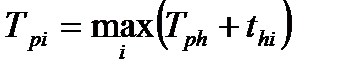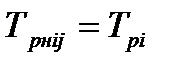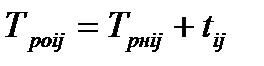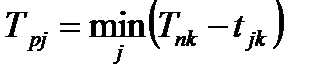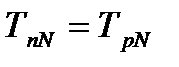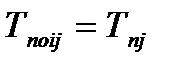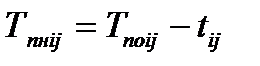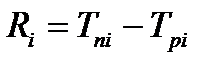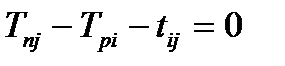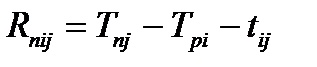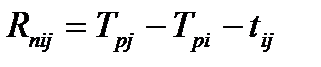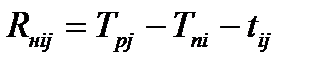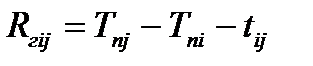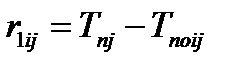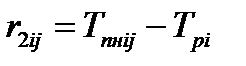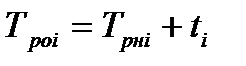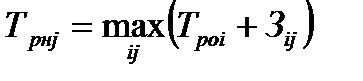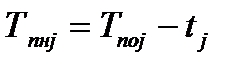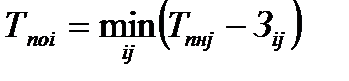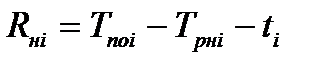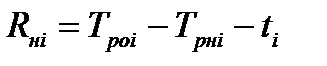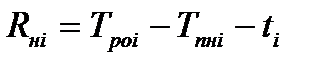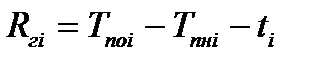Правила построения сетевых моделей
Единой последовательности построения сетевой модели (сетевого графика) нет. Строить модели можно по-разному – двигаясь от начала проекта (исходного события) к его окончанию (завершающему событию), и наоборот – от окончания к началу. Более логичным и правильным следует признать метод построения графиков от исходного события к завершающему, т.е. слева направо, так как при таком построении четко прослеживается технология выполнения моделируемых работ. Правила построения сетевой модели рассмотрим на примере модели вида «вершина – событие».
Они следующие:
1) правило последовательности изображения работ:сетевые модели следует строить от начала к окончанию, т.е. слева направо;
2) правило изображения стрелок: в сетевом графике стрелки, обозначающие работы, ожидания или зависимости, могут иметь различный наклон и длину, но должны идти слева направо, не отклоняясь влево от оси ординат, и всегда направляться от предшествующего события к последующему, т.е. от события с меньшим порядковым номером к событию с большим порядковым номером;
3) правило пересечения стрелок:при построении сетевого графика следует избегать пересечения стрелок: чем меньше пересечений, тем нагляднее график;
4) правило обозначения работ: в сетевом графике между обозначениями двух смежных событий может проходить только одна стрелка;
5) правило расчленения и запараллеливания работ (рис. 4.6.1): при построении сетевого графика можно начинать последующую работу, не ожидая полного завершения предшествующей. В этом случае нужно «расчленить» предшествующую работу на две, введя дополнительное событие в том месте предшествующей работы, где может начаться новая;
6) правило запрещения замкнутых контуров (циклов, петель) (рис. 4.6.2): в сетевой модели недопустимо строить замкнутые контуры – пути, соединяющие некоторые события с ними же самими, т.е. недопустимо, чтобы один и тот же путь возвращался в то же событие, из которого он вышел. На рисунке 4.6.б работы, соединяющие событий 2, 4 и 3 образуют замкнутый цикл, а работы, соединяющие события 2, 4, 5 и 3, – замкнутый контур;
7) правила запрещения тупиков (рис. 4.6.3): в сетевом графике не должно быть тупиков, т.е. событий, из которых не выходит ни одна работа, за исключением завершающего события;
8) правило запрещения хвостовых событий (рис. 4.6.4): в сетевом графике не должно быть хвостовых событий, т.е. событий, в которые не входит ни одна работа, за исключением начального события;
9) правило изображения дифференцированно-зависимых работ (рис. 4.6.5): если одна группа работ зависит от другой группы, но при этом одна или несколько работ имеют дополнительные зависимости или ограничения, при построении сетевого графика вводят дополнительные события. Допустим, есть две группы работ – а, б, в и г, д, е (рис. 4.6.5.а). Представим, что существует следующая зависимость между этими группами: работа г зависит от работ б и в, а работа д зависит только от работы б. Сетевая модель, объединяющая обе группы работ, которая приведена на рис. 4.6.5.б, не верна, так как сетевой график показывает, что работа д зависит, как от работы б, так и от работы в, а это противоречит исходной моделируемой технологии. Чтобы построить правильную сетевую модель, необходимо ввести дополнительное событие. Правильный сетевой график показан на рис. 4.6.5.в. В нем работы г и д являются дифференцированно-зависимыми и каждая имеет свою зависимость от предшествующих работ;
10) правило изображения поставки 4.6.6: в сетевом графике поставки (под поставкой понимается любой результат, который предоставляется «со стороны», т.е. не является результатом работы непосредственного участника проекта) изображаются двойным кружком либо другим знаком, отличающимся от знака обычного события данного графика. Рядом с кружком поставки дается ссылка на документ (контракт или спецификацию), раскрывающий содержание и условия поставки. Пример изображения поставки приведен на рис. 4.6.6. Но бывают и более сложные случаи. Например, на рис. 4.6.6.б. показана поставка, входящая в событие 2. Судя по графику, поставка необходима сразу для двух работ – 2–3 и 2–4. Но если нужно изобразить, что поставка требуется для работы 2–4, следует применить правило изображения дифференцированно-зависимых работ, т.е. ввести дополнительное событие (2') и зависимость (2–2') (рис. 4.6.6.в). Поставка теперь необходима только для работы 2'–4, что соответствует производственной технологии;
11) правило учета непосредственных примыканий (зависимостей): в сетевом графике следует учитывать только непосредственное примыкание (зависимость) между работами;
12) технологическое правило построения сетевых графиков: для построения сетевого графика необходимо в технологической последовательности установить:
- какие работы должны быть завершены до начала данной работы;
- какие работы должны быть начаты после завершения данной работы;
- какие работы необходимо выполнять одновременно с выполнением данной работы.
13) правила кодирования событий сетевого графика. Как было уже сказано, работа обозначается номерами начального и конечного событий – события, из которого работа выходит i, и события, в которое работа входит j, т.е. работа ограничена событиями i и j. Работа, предшествующая данной, обозначается как h–i, а последующая – как j–k. Время выполнения данной работы обозначается как tij, предшествующей работы – thi, последующей работы – tjk. Для кодирования сетевых графиков необходимо пользоваться следующими правилами:
- все события графика должны иметь свои собственные номера;
- кодировать события необходимо числами натурального ряда без пропусков;
- номер последующему событию следует присваивать после присвоения номеров предшествующим событиям;
- стрелка (работа) должна быть всегда направлена из события с меньшим номером в событие с большим номером.
Последовательность проставления цифр в кружки событий определяется нумерацией событий и направленностью стрелок.
|
|
| |
|
| |
|
| | Рисунок 4.6. Графическая иллюстрация ряда правил построения сетевой модели
| 4.2. Расчет аналитических параметров сетевых моделей вида «вершина – событие» с использованием метода критического пути
Расчет параметров сетевых моделей производится с помощью метода критического пути (МКП) (Critical Path Method – CPM). При этом при прямом проходе (слева направо) рассчитываются ранние сроки начала и окончания работ и ранние сроки свершения событий, а при обратном проходе (справа налево) – их поздние сроки.
При применении этого метода, как правило, применяются следующие обозначения (см. рис. 4.7):
tij – продолжительность рассматриваемой работы ij;
thi – продолжительность предшествующей работы hi;
tik – продолжительность последующей работы ik;
Трi – ранний срок свершения события i;
Тпi – поздний срок свершения события i;
Ткр – продолжительность критического пути;
Трнij – раннее начало работы ij;
Тпнij – позднее начало работы ij;
Троij – раннее окончание работы ij;
Тпоij – позднее окончание работы ij;
R – полный резерв времени пути;
Rпij – полный резерв времени работы ij;
Rcij – свободный резерв времени работы ij;
Rнij – независимый резерв времени работы ij;
Rгij – гарантированный резерв времени работы ij;
Ri – резерв времени события i;
r1ij – частный резерв времени работы ij I-го вида;
r2ij – частный резерв времени работы ij II-го вида.
|
| | Рисунок 4.7. Участок сети вида «вершина – событие»
| Ранний срок свершения события Трi – это минимальный срок, необходимый для выполнения всех работ, предшествующих данному событию. Он определяется максимальным значением суммы раннего срока свершения предшествующего события и продолжительностью предшествующей работы:
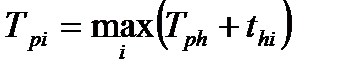
| (4.1)
| Для событий, не имеющих предшествующих работ, ранний срок свершения принимается равным нулю.
Ранний срок свершения событий определяет раннее начало последующих работ, например:
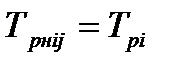
| (4.2)
| Ранее окончание работы определяется по формуле:
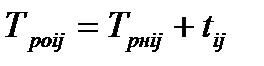
| (4.3)
| Поздний срок свершения события Тпj – это максимальный из допустимых моментов наступления данного события, при котором возможно соблюдение директивного (или расчетного) срока наступления завершающего события. Он определяется как наименьшее значение разницы между поздним свершением последующего события и продолжительностью последующей работы:
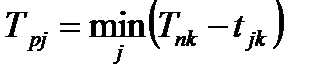
| (4.4)
| Для завершающего события сети принимается равенство:
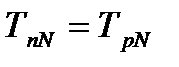
| (4.5)
| Позднее окончание предшествующей событию работы определяется поздним сроком свершения события:
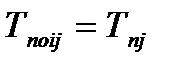
| (4.6)
| Позднее начало работы определяется по формуле:
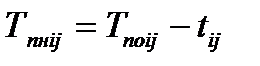
| (4.7)
| Резерв времени события Ri – это такой промежуток времени, на который может быть отсрочено наступление этого события без нарушения сроков завершения проекта в целом. Он определяется как разность между поздним и ранним сроками свершения события:
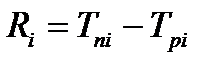
| (4.8)
| Критический путь – это наиболее протяженная во времени цепочка работ, ведущих от исходного к завершающему событию. Определение величины критического пути ведется от исходного события к завершающему. Необходимым условием того, что работа находится на критическом пути, является нулевой резерв времени начального и конечного события этой работы:
Резервы времени работ определяются только у работ, не лежащих на критическом пути. Работы, лежащие на критическом пути, не имеют никаких резервов времени, т.е. у этих работ все резервы (полный, свободный, независимый и гарантированный) равны нулю.
Полный резерв времени работы Rпij – это весь резерв времени, которым обладает работа при условии возможного раннего ее начала и допустимого позднего ее окончания. Он определяется по формуле:
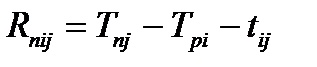
| (4.9)
| Свободный резерв времени работы Rсij – это весь резерв времени только данной работы, позволяющей увеличить продолжительность работы на величину свободного резерва, не вызвав изменений ранних сроков свершения последующих событий и работ при условии раннего окончания предшествующих работ. Он определяется по формуле:
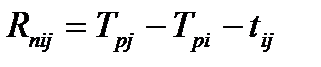
| (4.10)
| Независимый резерв времени работы Rнij – это весь резерв времени только данной работы (часть ее полного резерва), позволяющей увеличить продолжительность работы на величину независимого резерва, не вызвав изменений ранних сроков свершения последующих событий и работ, при условии позднего окончания предшествующих работ. Он определяется по формуле:
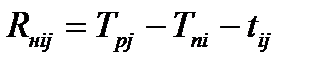
| (4.11)
| Гарантированный резерв времени работы Rгij – это весь резерв времени только данной работы, позволяющей увеличить продолжительность работы на величину гарантированного резерва, не вызвав изменений поздних сроков свершения последующих событий и работ, при условии позднего окончания предшествующих работ. Он определяется по формуле:
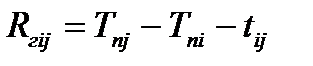
| (4.12)
| Частный резерв времени работы первого вида rIij показывает, какая часть полного резерва может быть использована для увеличения продолжительности работы не влияя на поздний срок свершения конечного события этой работы. Он определяется по формуле:
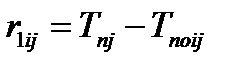
| (4.13)
| Частный резерв времени работы второго вида rIIij показывает, какая часть полного резерва может быть использована для увеличения продолжительности работы не влияя на ранний срок свершения начального события этой работы. Он определяется по формуле:
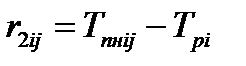
| (4.13)
| 4.3. Расчет аналитических параметров сетевых моделей вида «вершина – работа»
Расчет аналитических параметров сети вида «вершина – работа» подобен расчету, описанному выше.
Графически участок такой сети можно представить, как это показано на рисунке 4.8.
|
| | Рисунок 4.8. Участок сети вида «вершина – работа»
| В модели применяются следующие обозначения:
ti – продолжительность работы i;
Ткр – продолжительность критического пути;
Трнj – раннее начало работы i;
Тпнi – позднее начало работы i;
Троi – раннее окончание работы i;
Тпоi – позднее окончание работы i;
R – полный резерв времени пути;
Rпi – полный резерв времени работы i;
Rci – свободный резерв времени работы i;
Rнi – независимый резерв времени работы i;
Rгi – гарантированный резерв времени работы i;
З ij – задержка между работами ij.
Срок раннего начала самой первой работы в сети принимается равным нулю. А срок позднего окончания самой последней работы в сети принимается равным сроку раннего окончания этой работы.
Для расчета аналитических параметров сетевой модели вида «вершина – работа» используются следующие формулы:
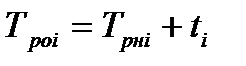
| (4.14)
| 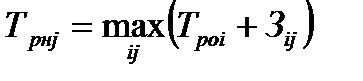
| (4.15)
| 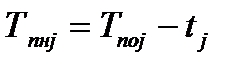
| (4.16)
| 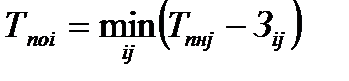
| (4.17)
| 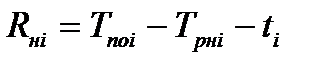
| (4.18)
| 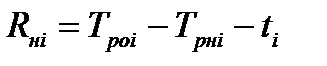
| (4.19)
| 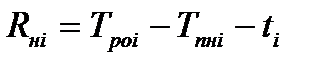
| (4.20)
| 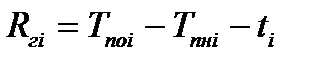
| (4.21)
|
Date: 2015-05-18; view: 1568; Нарушение авторских прав | Понравилась страница? Лайкни для друзей: |
|
|