
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Горных пород
|
|
Наиболее распространёнными графическими представлением анализов гранулометрического состава горных пород (табл. 3.2) являются гистограммы, циклограммы, графики треугольники и интегральные (кумулятивные) кривые.
Таблица 3.2
Результаты гранулометрического анализа горных пород
| № анализа | Размер фракций, мм / Процентное содержание частиц, % | ||||||||
| 2–1 | 1–0,5 | 0,5–0,25 | 0,25–0,1 | 0,1–0,05 | 0,05–0,01 | 0,01–0,005 | 0,005–0,001 | Менее 0,001 | |
| − | − |
Гистограмма – столбчатая диаграмма, один из видов графического изображения статистического распределении каких-либо величин по количественному признаку. Гистограмма представляет собой совокупность смежных прямоугольников, построенных на прямой линии.
Для изображения на гистограмме гранулометрического состава горных пород на вертикальной оси откладывают процентное содержание фракций, а на горизонтальной оси – произвольно выбранные равные отрезки.
На отрезках, соответствующих каждой фракции, строится как на основании прямоугольник высотой, равной процентному содержанию частиц во фракции.
Гистограмма, изображающая гранулометрический состав горной породы анализа № 1 представлена на рис. 3.1.
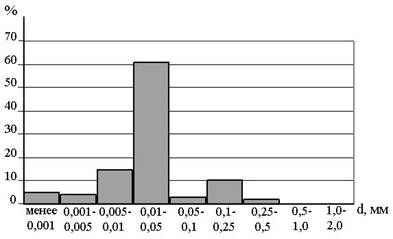
Рис. 3.1. Гистограмма гранулометрического состава пород анализа №1
При построении циклограмм, характеризующих гранулометрический состав горных пород, вычерчивается окружность произвольного радиуса. Площадь окружности принимается за 100 %. Величина отдельной фракции показывается в виде сектора, площадь которого пропорциональна ее процентному содержанию. Сектора заштриховываются в соответствии с принятыми к фракциям условным обозначениям.
Циклограмма, изображающая гранулометрический состав горной породы анализа № 1 представлена на рис. 3.2.
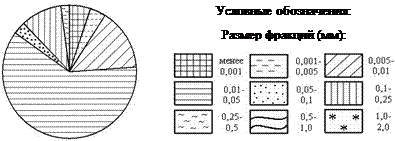
Рис. 3.2. Циклограмма гранулометрического состава пород анализа №1
Графические изображения результатов гранулометрического анализа в виде гистограмм и циклограмм имеют существенный недостаток, который заключается в невозможности изображения результатов массовых определений гранулометрического состава на одной гистограмме или циклограмме.
График-треугольник (см. приложение 1) представляет собой равносторонний треугольник, каждая сторона которого разделена на 100 равных частей. Если принять, что каждая из вершин треугольника отражает нулевое содержание одной из основных фракций, тогда по углам треугольника будет отмечаться стопроцентное содержание этих фракций. Линии, параллельные сторонам, будут соответствовать процентному содержанию той или иной фракции, а это значит, что точка внутри треугольника будет соответствовать составу породы.
По положению точки внутри графика – треугольника можно судить о распределении фракции в горной породе и в зависимости от этого дать определение породы.
График-треугольник гранулометрического состава горной породы анализа № 1 представлен на рис. 3.3.
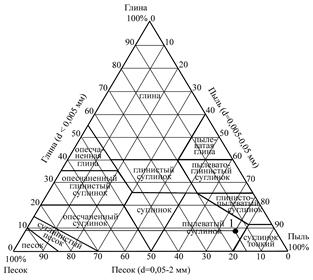 |
Рис. 3.3. График-треугольник гранулометрического состава горной породы анализа № 1
Анализируя расположение точки 1 внутри графика – треугольника, можно сделать вывод, что рассматриваемая порода относится к пылеватым суглинкам.
Интегральные (кумулятивные) кривые гранулометрического состава строятся в прямоугольной системе координат в полулогарифмическом масштабе (когда по одной оси задается логарифмический масштаб, а по другой – линейный).
Использование полулогарифмического масштаба вызвано тем, что при гранулометрическом анализе частицы подразделяются на фракции, размеры которых убывают в геометрической прогрессии. По оси абсцисс откладываются логарифмы диаметров фракций частиц, а по оси ординат – содержание данной фракции в породе в процентах.
Для удобства определения логарифмов диаметров частиц переводят эти размеры из миллиметров в микроны для того, чтобы не получать отрицательных логарифмов (табл. 3.3).
Таблица 3.3
Исходные данные для построения кумулятивной кривой
гранулометрического состава горных пород
| Фракция | Сумма фракций | Расчетные значения | |||
| Диаметр частиц, мм | Содержание частиц, % | Диаметр частиц, мм | Содержание частиц, % | Логарифм диаметра частиц, lg d | Расстояние от начала оси абсцисс, см |
| 0,001 | |||||
| 0,001–0,005 | 0,7 | 2,3 | |||
| 0,005–0,01 | 1,0 | 3,3 | |||
| 0,01–0,05 | 1,7 | 5,6 | |||
| 0,05–0,1 | 2,0 | 6,6 | |||
| 0,1–0,25 | 2,4 | 7,9 | |||
| 0,25–0,5 | 2,7 | 8,9 | |||
| 0,5–1,0 | 3,0 | 9,9 | |||
| 1,0–2,0 | 3,3 | 12,0 |
Для построения логарифмической шкалы по оси абсцисс от начальной точки в некотором масштабе откладываются отрезки, равные десятичным логарифмам ряда чисел. Если отложено число, равное lg d, то около соответствующей точки ставится d. Около начальной точки должна стоять пометка 1, т.к. lg 1 = 0. Таким образом, на логарифмической шкале расстояние от пометки 1 до пометки d равно в выбранном масштабе lg α.
Так как lg (10d) = 1+ lg d, то пометки на логарифмической шкале на участке от 10 до 100 будут в точности соответствовать пометкам на участке от 1 до 10. Это же рассуждение может быть проведено и для других участков шкалы. Поэтому, для изображения чисел от 1 до 100 на логарифмической оси требуется увеличить длину оси всего в два раза по сравнению с осью, размеченной от 1 до 10.
При построении кумулятивных кривых гранулометрического состава горных пород, диапазон изменений диаметра частиц превышает их порядок (dмин = 1 мк, dмах = 2000 мк). Таким образом, на оси абсцисс необходимо отобразить числа от 1 до 2000. Целесообразно разделить ось на 4 декады, включающие диаметры 1–10 мк, 10–100 мк, 100–1000 мк и 1000–2000 мк. Примем длину оси равной 12 см, тогда на одну декаду будет приходиться 3 см. Соответственно, деление 5 должно стоять на расстоянии L = lg5 × 3 = 2,1 см от начала оси абсцисс, деление 50 – на расстоянии L = lg50 × 3 = 5,1 см, деление 500 – на расстоянии L = lg500 × 3 = 8,1 см.
Процентное содержание по оси ординат откладывают, начиная с самой мелкой фракции. Для каждой последующей фракции величину ординаты получают последовательным суммированием данных для предыдущих размеров, т.е. к процентному содержанию предыдущей фракции прибавляют процентное содержание следующей и т.д. (см. табл. 3.3).
Таким образом, каждая точка графика дает суммарное количество частиц данного размера и размеров, меньших, чем этот размер. По пересечению диаметров частиц строят кривую, которая называется кумулятивной кривой (рис. 3.4).
Кумулятивные кривые позволяют определить действующий или эффективный и контролирующий диаметры частиц и вычислить на их основе коэффициент неоднородности, показывающий степень отсортированности пород.
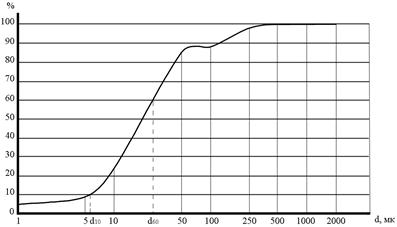
Рис. 3.4. Кумулятивная кривая гранулометрического состава горной породы
Коэффициент неоднородности (Кн) представляет собой отношение величины контролирующего диаметра частиц (d60) к величине действующего их диаметра (d10):
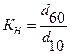 (3.1)
(3.1)
Действующим (эффективным) диаметром частиц является такой диаметр, меньше которого в породе содержится 10 % частиц.
Контролирующим диаметром называется диаметр, меньше которого в породе 60 % частиц.
Для определения действующего и контролирующего диаметров частиц, из точек на оси ординат, соответствующих 10 и 60 % их содержанию проводятся линии, параллельные оси абсцисс до пересечения с кумулятивной кривой. Из точек пересечения опускаются перпендикуляры на ось абсцисс (см. рис. 5.4) и определяются значения диаметров частиц. Значение коэффициента неоднородности определяется с точностью до запятой.
Для определения диаметров частиц необходимо определить расстояние от места пересечения соответствующих перпендикуляров до начала оси абсцисс (L). Диаметр частиц определится из выражения lg d = L/3.
В нашем случае:
lg d10 = 2,5/3; d 10 = 100,8 = 6 мк = 0,006 мм;
lg d60 = 4,4/3; d 10 = 101,5 = 32 мк = 0,032 мм.
Коэффициент неоднородности не может быть меньше единицы и практически не бывает больше 200. Чем меньше его величина − тем однороднее порода. Принято, что при Кн = 5 порода считается однородной и для нее характерно ламинарное движение подземных вод. Если Кн > 5, то порода считается неоднородной по гранулометрическому составу, и подземные воды в ней имеют турбулентный характер движения.
В нашем случае:
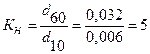 .
.
Так как Кн > 5, то горная порода по гранулометрическому составу считается неоднородной, и подземные воды в ней имеют турбулентный характер движения.
Date: 2015-04-23; view: 2790; Нарушение авторских прав