Храбров Е. А. 1 page

Гомельский государственный технический университет

Имени П. О. Сухого

Кафедра "Промышленная электроника"

Е. А. Храбров

Основы цифровой электроники

Практическое пособие

по курсу "Электронные цепи дискретного действия"

для студентов специальности 36.04.02

"Промышленная электроника"

Гомель 2003

УДК 621. 397

Храбров Е. А.

Основы цифровой электроники: Практическое пособие по курсу "Электронные цепи дискретного действия" для студентов специальности 36.04.02 "Промышленная электроника". – Гомель: ГГТУ, 2003. – 86 с.

Рецензенты: –Заведующий кафедрой "Информационные технологии" Гомельского филиала Международного института трудовых и социальных отношений (МИТСО), кандидат технических наук, доцент Кудин В. П.

–Доцент кафедры "Автоматизированный электропривод" ГГТУ имени П.О. Сухого, кандидат технических наук, Погуляев М.Н.

ã Гомельский государственный технический университет

имени П. О. Сухого, 2003

ВВЕДЕНИЕ

Учебным планом подготовки по специальности 36.04.02 "Промышленная электроника" установлена дисциплина "Электронные цепи дискретного действия". Цель дисциплины, – изучение студентами теоретических основ анализа и синтеза электронных цифровых и импульсных устройств на интегральных цифровых микросхемах малой и средней степени интеграции. В результате изучения первой половины данного курса, которая называется "Основы цифровой электроники", студенты должны усвоить следующие вопросы:

1. Двоичные сигналы и системы счисления в цифровой электронике.

2. Алгебра логики; положительная и отрицательная логика.

3. Минимизация логических функций; построение комбинационных логических схем по заданным булевым выражениям.

4. Классификация, обозначения цифровых микросхем, их параметры.

5. Состав и схемотехника ТТЛ логических микросхем.

6. Состав и схемотехника КМОП логических микросхем.

7. Особенности схем эмиттерно–связанной логики.

В настоящем учебном пособии излагаются основные теоретические сведения в соответствии с программой курса, часть прикладных вопросов изложена в практических руководствах по выполнению лабораторных работ по данной дисциплине.

В данном пособии описываются элементарные логические функции и показано, как с помощью этих простых функций можно получить достаточно сложные выражения, описывающие требующиеся по техническим заданиям цифровые устройства.

Ввиду различий в условных графических обозначениях логических элементов, встречающихся в технической литературе, в настоящем пособии приводятся четыре варианта этих обозначений:

– отечественные, в соответствии с ГОСТ 2.743–82;

– старые зарубежные обозначения, которые до настоящего времени встречаются в иностранной технической литературе;

– обозначения в соответствии с американской системой MILSPEC;

– обозначения в соответствии с системой, рекомендованной Международной Электротехнической Комиссией (МЭК) и широко распространенной особенно среди европейских производителей электронной техники.

1. Достоинства и недостатки цифровой электроники

Когда сигналы, с которыми приходится иметь дело, либо являются непрерывными по самой своей природе (например, звуковые), либо представляют собой непрерывно меняющееся напряжение, поступающее от измерительных приборов (например, от устройств для измерения температуры или светового излучения, биологических или химических зондов), то естественным является применение для их обработки аналоговых устройств.

Входной сигнал по своей природе может быть и чисто дискретным, например импульсы в детекторе частиц или "биты" информации, поступающие от ключа, клавиатуры или ЭВМ. В подобных случаях естественно и удобно использовать цифровую электронику.

Но все чаще и аналоговые сигналы стараются обрабатывать цифровыми устройствами. Причины, обусловливающие переход от аналоговых систем к цифровым системам, весьма разнообразны. Пожалуй, самым очевидным достоинством цифровых систем является снижение требований, предъявляемых к выходному сигналу двоичной схемы, по сравнению с выходом аналоговой схемы.

Информация в аналоговой схеме представлена в виде величины напряжения, и любые отклонения от требуемого значения, даже самые малые, приводят к потере, искажению информации. С двоичной схемой связан всего лишь один бит информации, значение которого определяется тем, в каком из двух возможных состояний находится выход схемы.

Рассмотрим передачу фиксированного количества информации, например 20 бит, посредством аналогового сигнала. Каждый бит информации позволяет сделать выбор между двумя равновероятными вариантами; поэтому с использованием 20 бит информации можно представить 2²⁰ = 1 048 576 возможных вариантов. Таким образом, весь диапазон выходного сигнала делят на 1 048 576 равных частей и, определяя, в какой части этого диапазона находится аналоговый выходной сигнал, выделяют 20 бит информации.

Для диапазона напряжений 0... 10 В приращение (шаг квантования) составляет 10 мкВ, и сконструировать реальную схему с такой точностью в пределах обычно существующих помех и диапазона изменения рабочих температур практически невозможно или по крайней мере неоправданно дорого. Один из вариантов решения проблемы заключается в использовании 20 двоичных схем, каждый выход которых несет 1 бит информации. Хотя это и ведет к увеличению числа используемых схем, зато стоимость каждой такой схемы, а в результате и всего устройства, значительно снижается. Очевидно, что при обработке большого количества информации из–за разницы в стоимости предпочтение отдается двоичным, цифровым схемам.

Примером этого может служить переход к цифровым способам управления в бытовых телевизионных приемниках. Здесь практически все параметры телевизионного изображения и звука регулируются в настоящее время дискретно, устанавливаясь на одном из 64 допустимых уровней.

Управляющий сигнал поступает в телевизор, как правило, через систему дистанционного управления с помощью инфракрасного канала, передающего кодированные цифровые данные о кнопках, нажатых на переносном пульте для изменения того или иного параметра в телевизоре. В самом телевизоре значения всех параметров запоминаются в цифровом запоминающем устройстве, и хранится в нем сколь угодно долго. Такой стабильности и сохранности выбранных параметров настройки очень трудно было бы добиться аналоговыми средствами.

Другим не менее наглядным примером вытеснения аналоговых способов обработки информации цифровыми является широкое распространение так называемых компакт дисков с лазерным считывающим устройством для высококачественной записи и воспроизведения музыки. Таким образом, магнитофоны и проигрыватели граммофонных пластинок заменяются CD ROM проигрывателями.

Применяемые в них сложные алгоритмы устранения шумов и помех в воспроизводимых записях не приводят к существенному повышению стоимости этих устройств, т. к. вся цифровая обработка информации производится всего несколькими микросхемами большой интеграции (а порой и одной микросхемой), цена которых несравнимо ниже стоимости всего проигрывателя. Значительные первоначальные затраты на разработку вышеупомянутых алгоритмов и реализующих их микросхем сравнительно быстро окупились за счет массового производства проигрывателей.

Использование цифровой оперативной памяти для запоминания текущего фрагмента записи с целью устранения искажений, вносимых устройством считывания при тряске и вибрациях для носимых и возимых CD ROM проигрывателей, позволяет добиться высококачественного воспроизведения надежными и недорогими средствами.

Можно считать, что цифровые способы обработки сигналов предпочтительнее применять в тех случаях, когда:

– входные сигналы имеют дискретный характер;

– требуется сложная и нелинейная обработка сигналов при массовом производстве устройств обработки сигналов.

2. Двоичные сигналы

Сигналы можно разделить на две класса:

– аналоговые, непрерывные, изменяющиеся плавно;

– дискретные, изменяющиеся скачками обычно в определенные моменты времени.

Множество допустимых уровней дискретного сигнала может быть любым, однако есть один самый распространенный тип дискретного сигнала, у которого возможны только два значения: ВЫСОКИЙ (HIGH, 1) и НИЗКИЙ (LOW, 0) уровни. Такой сигнал называют двоичным, а зачастую цифровым (строго говоря, цифровой сигнал может иметь не только два уровня).

Двоичные (цифровые) сигналы можно подразделить на числоимпульсные, последовательные и параллельные позиционные сигналы.

Самыми простыми двоичными сигналами являются числоимпульсные сигналы, у которых информационным параметром является количество импульсов N за время заданного постоянного интервала времени, или за время между двумя определенными метками времени, причем ни длительность импульсов, ни их расположение при этом не имеют значения. На рис.2.1.1 показан пример числоимпульсного двоичного сигнала, в котором отметками начала и конца интервалов, в которых производят подсчет числа импульсов сигнала, служат достаточно длительные паузы между пачками импульсов. Такой вид может иметь сигнал набора номера в телефонных аппаратах с импульсным набором, которые распространены в нашей стране.

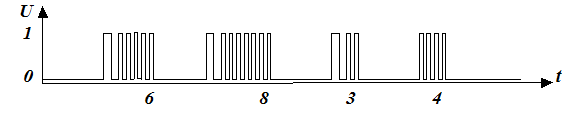
Рис. 2.1.1. Пример числоимпульсного двоичного сигнала, содержащего 6, 8, 3 и 4 импульса соответственно в первой, второй, третьей и четвертой посылках.

Числоимпульсные сигналы настолько просты, что как правило, когда говорят о двоичных или цифровых сигналах, то подразумевают при этом один из двух позиционных видов двоичного сигнала, – последовательный, или параллельный двоичный сигнал, для которых уже имеет значение и длительность и положение каждого единичного импульса.

В последовательном двоичном сигнале информация заключена во временной последовательности появления нулей и единиц внутри своей группы, приходящейся на определенное число тактов дискретного времени. В каждой такой группе первая позиция обычно соответствует самому младшему разряду, имеет самый малый вес, а все последующие позиции (номера дискретного времени внутри группы) имеют последовательно нарастающие веса вплоть до последней позиции с максимальным весом, соответствующей старшему разряду. Поскольку в двоичном сигнале имеется только два допустимых значения, то все веса, разряды кода являются степенями двойки.

На рис. 2.1.2 показан пример последовательного двоичного сигнала, поступающего с одного вывода какого–то цифрового устройства CU. На этом рисунке, кроме сигналов по тактовой линии и самого последовательного двоичного сигнала, показано также цифровое устройство CU с его входами и выходом. Под каждым тактовым отрезком времени приведены их весовые коэффициенты.

Рис. 2.1.2. Пример последовательного двоичного сигнала, поступающего с одного вывода цифрового устройства CU, где:

а) – сигнал, передаваемый по тактовой линии;

б) – последовательность нулей и единиц, в первом интервале соответствующая числу 20, а во втором, – 26.

Последовательные двоичные сигналы хорошо использовать при передаче данных на большие расстояния, когда прокладывать многожильный кабель для параллельного двоичного сигнала становится достаточно дорого, ведь в отличие от последовательного параллельный сигнал передается одновременно по нескольким линиям, как это показано на рис.2.1.3. В приведенном примере параллельного сигнала совокупность нулей и единиц во время первого тактового импульса соответствует числу 3, а во втором, – 10.

Обычно передача цифровых данных на расстояние до нескольких метров производится с помощью параллельных сигналов, а на большие расстояния, – с помощью последовательных сигналов.

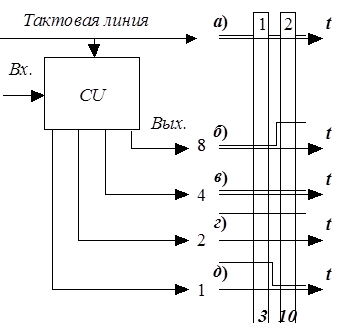
Рис.2.1.3. Пример параллельного двоичного сигнала, поступающего одновременно с нескольких выводов цифрового устройства CU, в котором:

а) – сигнал, передаваемый по тактовой линии;

б) – сигнал, поступающий со старшего выхода цифрового устройства CU, которому соответствует весовой коэффициент 8;

в) – сигнал, поступающий со среднего выхода цифрового устройства CU, которому соответствует весовой коэффициент 4;

г) – сигнал, поступающий со среднего выхода цифрового устройства CU, которому соответствует весовой коэффициент 2;

д) – сигнал, поступающий с младшего выхода цифрового устройства CU, которому соответствует весовой коэффициент 1.

Как видно из трех вышеприведенных рисунков, самым быстрым способом передачи информации является использование параллельного сигнала, но при этом требуются самые большие аппаратные затраты.

Самым медленным, но зато и самым простым и требующим самые малые затраты оборудования, является применение числоимпульсного сигнала.

Последовательный позиционный двоичный сигнал является промежуточным между параллельным и числоимпульсным сигналами.

3. СИСТЕМЫ СЧИСЛЕНИЯ В ЦИФРОВОЙ ЭЛЕКТРОНИКЕ

Все современные системы счисления (кроме некоторых римских цифр) являются позиционными, т.е. в них одна и та же цифра в разных позициях (слева, справа) имеет разное значение. Например, в десятичном числе 55 левая цифра означает 50, а правая, – только 5. В общем виде в позиционной системе счисления с основанием системы Х число А можно представить в виде:

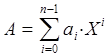
где n – количество разрядов числа А, а_i – коэффициенты каждого разряда, которые могут принимать значения от 0 до Х – 1.

При необходимости основание системы счисления указывается внизу после числа в виде нижнего индекса.

Примеры записи чисел в некоторых системах счисления:

1. Четырехразрядное десятичное число:

5685₁₀ = 5×10³ + 6×10² + 8×10¹ + 5×10⁰,

где Х = 10, – основание системы счисления, а ₀ = 5, а ₁ = 8, а ₂ = 6,

а ₃ = 5, – коэффициенты в каждом разряде, n = 4, – количество разрядов числа А.

2. Трехразрядное восьмеричное число:

372₈ = 3×8² + 7×8¹ + 2×8⁰ = 250₁₀

где Х = 8 (восьмеричная система счисления), коэффициенты в разрядах числа A: а ₀ = 2, а ₁ = 7, а ₂ = 3; n = 3, – количество разрядов числа А.

3. Двухразрядное шестнадцатеричное число:

4E₁₆ = 4×16¹ + 14×16⁰ = 78₁₀

где Х = 16 (шестнадцатеричная система счисления), коэффициенты в разрядах числа А а ₀ = E = 14, а ₁ = 4 (шестнадцатеричные цифры от 0 до 9 записываются так же, как и соответствующие десятичные цифры, а шестнадцатеричные цифры 10, 11, 12, 13, 14, 15 записываются заглавными латинскими буквами А, В, С, D, Е, F соответственно); n = 2, – количество разрядов числа А.

4. Четырехразрядное двоичное число:

1101₂ = 1×2³ + 1×2² + 0×2¹ + 1×2⁰ = 13₁₀

где X = 2, – двоичная система счисления, коэффициенты в разрядах числа А: а ₀ = 1, а ₁ = 0, а ₂ = 1, а ₃ = 1, n = 4, – количество разрядов числа А.

Двоичный разряд, который может принимать только два значения: 0 или 1, называют "бит", происходящее от сокращения BIT английских слов

BI NARY DIG IT – "двоичная цифра". В английском языке слово bit означает также кусочек.

Десятичная система, к которой мы привыкли, основана на количестве пальцев рук и для применения в цифровой технике неудобна. В цифровой аппаратуре устройства обычно имеют два рабочих состояния и в них применяют двоичную систему счисления. Чем меньше основание системы счисления, тем менее компактный вид имеет запись какого-то числа, поэтому для сокращенной записи двоичных чисел обычно используют восьмеричную или шестнадцатеричную системы счисления. Восьмеричная и шестнадцатеричная системы счисления применяются в вычислительной технике из–за удобства представления больших двоичных чисел, поскольку их основания являются степенями двойки. Они являются как бы компромиссными между двоичной и десятичной системами счисления.

Преобразовать десятичное число в двоичное можно путем деления на 2 сначала самого числа, а затем каждого промежуточного частного. При этом каждый неделимый остаток дает очередную цифру соответствующего разряда искомого двоичного числа. Первый полученный таким образом остаток даст цифру младшего разряда, а последний, – старшего разряда двоичного числа. Например, десятичное число 53₁₀ преобразуем в двоичное:

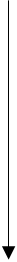
53: 2 = 26 + 1

26: 2 = 13 + 0

13: 2 = 6 + 1

6: 2 = 3 + 0

3: 2 = 1 +1

1: 2 = 0 +1

1 1 0 1 0 1₂

Аналогично можно преобразовывать числа с другими основаниями.

На основе двоичной системы счисления в цифровой технике разработаны различные формы представления чисел, которые иногда называют кодами. Естественную запись двоичного числа называют двоичным кодом.

Так же, как большие десятичные числа для удобства чтения разбивают при записи на тройки, так и большие двоичные числа обычно разбивают на четверки, – тетрады. Две тетрады или восемь двоичных цифр называют байт, – BYTE. Число 2¹⁰ = 1024 называют в цифровой технике словом "килобит" в нарушение точного значения данного слова, – 1000.

В цифровой аппаратуре, в основном при индикации показаний десятичными цифрами или при задании параметров десятичными задатчиками, широко применяются различные двоично–десятичные коды.

Самый распространенный из них BCD код (сокращенное BINARY CODED DECIMAL, – двоично-кодированная десятичная цифра), который порой называют позиционным 8421–кодом, или натуральным двоично–десятичным кодом. В этом коде каждая десятичная цифра представляется своей отдельной тетрадой, – четверкой двоичных цифр, например:

5 2 6

526 ₁₀ = 0101 0010 0110 _BCD

С помощью 4-х битов можно составить 16 различных сочетаний единиц и нулей, а для десятичных цифр достаточно 10 сочетаний. 6 сочетаний избыточны, поэтому возможны различные позиционные двоично-десятичные коды. Отличаются эти коды порядком следования степеней основания в представлении десятичных цифр. Так BCD код имеет следующие веса разрядов:

2³, 2², 2¹, 2⁰ = 8421.

Другой позиционный двоично–десятичный код, – код Эйкена имеет следующие веса разрядов:

2¹, 2², 2¹, 2⁰ = 2421.

Десятичное число 9₁₀ , записанное в BCD–коде, равно 1001_BCD, а это же число, записанное в коде Эйкена, имеет следующий вид: 1111_ЭЙКЕН .

Еще один распространенный двоично–десятичный код, – код с избытком 3 (EXCESS – 3 CODE). В нем каждая десятичная цифра кодируется двоичной тетрадой, в которой взвешенная сумма разрядов больше этой десятичной цифры на три. Так, десятичная цифра 9 записывается тетрадой 1100, для которой взвешенная сумма разрядов 8×1 + 4×1 + 2×0 + 1×0 = 12, что на 3 больше 9.

Этот код называют самодополняющимся до 10, т.е. его младшие 5 цифр (от 0 до 4) являются зеркальным отражением, инверсией старших 5 цифр (от 5 до 9); например, число 0 = 0011_EX3 является инверсным числу 9 = 1100_EX3, число 1 = 0100_EX3 является инверсным числу 8 = 1011_EX3 и т.д. Достоинством кода с избытком 3 является его повышенная надежность при передаче информации в канале связи, поскольку количество единиц в его числах в среднем равно количеству нулей.

В двоично–кодированных датчиках перемещения или угла поворота часто применяется код Грея (GRAY CODE). В этом коде комбинации двоичных цифр, представляющие числа, соседние по величине, отличающиеся лишь в одной кодовой позиции, т.е. при последовательном переходе от одного числа к другому всегда изменяется только один из двоичных разрядов.

Число B, записанное в двоичном коде, можно преобразовать в число G в коде Грея с помощью следующего выражения:

G_i = B_i Å B_i+1.

Число G, записанное в коде Грея, можно преобразовать в число B в двоичном коде с помощью следующего выражения:

B_i = G_i Å B_i+1.

Здесь знак Å означает сумму по модулю два, которая равна единице, если входные слагаемые разные, или, – нулю, если они одинаковые, т.е.:

0 Å 0 = 0

0 Å 1 = 1

1 Å 0 = 1

1 Å 1 = 0

Число в коде Грея можно также получить из двоичного кода следующим образом:

двоичный код 1 1 0 1 0 1

Å Å Å Å Å

код Грея 1 0 1 1 1 1

Обратное преобразование кода Грея в двоичный код производят по похожей схеме:

код Грея 1 0 1 1 1 1

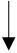
Å Å Å Å Å

двоичный код 1 1 0 1 0 1

Свойство кода Грея изменяться только в одном разряде при последовательном переходе от одного числа к другому ближнему определяет его преимущество перед другими кодами при использовании этого кода для построения кодирующих дисков и пластин. Очевидно, что такое свойство кода уменьшает число переключений считывающих устройств и снижает неоднозначность считывания кода. Код Грея нельзя отнести к позиционным кодам, поскольку в нем весовые значения единиц в различных позициях нельзя однозначно определить по формуле, приведенной в начале данного раздела.

4. АЛГЕБРА ЛОГИКИ

Называемая в честь английского математика Дж. Буля булевой алгеброй, алгебра логики составляет теоретическую основу логики, теории алгоритмов и логического проектирования цифровых схем. От обычной, привычной нам алгебры, булева алгебра отличается тем, что ее логические аргументы (переменные) могут принимать лишь два значения, а основных функций в булевой алгебре всего три: логическое умножение И, логическое сложение ИЛИ и отрицание НЕ.

Два возможных значения логических переменных называют ИСТИНА (TRUE) и ЛОЖЬ (FALSE), иногда их называют ДА и НЕТ, а чаще всего их обозначают соответственно как 1 и 0. При этом следует помнить, что эти логические 0 и 1 не надо трактовать как числа, над ними нельзя производить арифметические действия.

Date: 2015-05-09; view: 611; Нарушение авторских прав