Massless Dirac equation

We briefly discuss here the relation between the massless Dirac spectrum of graphene and lowenergy electronic states of nanoribbons. The electronic states near the two non-equivalent Dirac points (K ±) can be described by 4×4 Dirac equation, i.e.

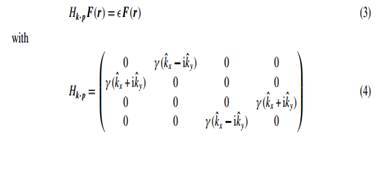
Here, 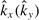is a wavevector operator, and can be replaced by k ^ˆ → −i∇ˆ in the absence of

magnetic field. γ is a band parameter, which satisfies γ = √3 ta /2. F _A ^{K ±}(r) and F _B ^{K ±}(r) are the envelope functions near K ± points for A and B sublattices, which slowly vary in the length scale of the lattice constant. We can rewrite the above effective mass Hamiltonian by using the Pauli matrices τ ^{x , y, z} for valley space (K ±) as

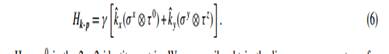
Here, τ⁰ is the 2×2 identity matrix. We can easily obtain the linear energy spectrum for grapheme

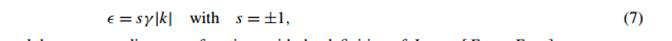and the corresponding wave functions with the definition of 8 _K ± = [ F _K ±_A, F _{K ±}B] are

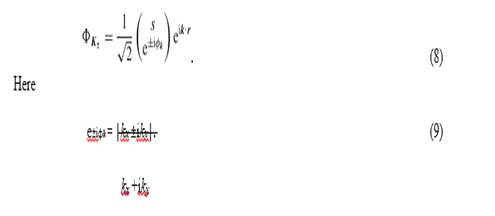
2.2.1. Zigzag nanoribbons. The low-energy electronic states for zigzag nanoribbons can also be described starting from the Dirac equation [10, 71]. Since the outermost sites along the first (N th) zigzag chain are B(A)-sublattice, an imbalance between two sublattices occurs at the zigzag edges leading to the boundary conditions

φ K ± A(r [0]) = 0, φ K ± B(r [ N +1]) = 0, (10)

where r _{[ i ]} stands for the coordinate at the i th zigzag chain. The energy eigenvalue and wavenumber is given by the following relation:

ε = ±(η− k)e^{η W}, (11)

where η = √ k ² −ε. It can be shown that the valley near k = 3π/2 a in figure 1(b) originates from the K ₊-point, the other valley at k = −3π/2 a from the K −-point [10, 71].

2.2.2. Armchair nanoribbons. The boundary condition of armchair nanoribbons projects K ₊ and K − states into the 0 point in the first BZ as can be seen in figure 2(b). Thus, the lowenergy states for armchair nanoribbons are the superposition of K ₊ and K − states. The boundary condition for armchair nanoribbons [71] can be written as

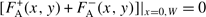, (12)

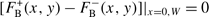. (13)

If the ribbon width W satisfies the condition of W = (3/2)(N _w +1) a with N _w = 0,1,2,..., the system becomes metallic with the linear spectrum. The corresponding energy is given by

n, k, s 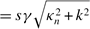, (14)

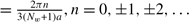where κ _n and s = ±. The n = 0 mode is the lowest linear subband for metallic armchair ribbons. The energy gap (1_s) to the first parabolic subband of n = 1 is given as

1_s = 4πγ/3(N _w +1) a, (15)

which is inversely proportional to ribbon width. It should be noted that a small energy gap can be acquired due to the Peierls distortion for half-filling at low temperatures [69, 70], but such an effect is not relevant for single-channel transport in the doped energy regime.

Date: 2015-05-09; view: 621; Нарушение авторских прав