
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Теория центральных мест В. Кристаллера и А. Леша
|
|
В рамках теории размещения сложилась другая система взглядов, противоположная веберианской, исходящая из относительно равномерного размещения экономической активности в пространстве. Эта система представлена теорией центральных мест В.Кристаллера – «Центральные места в Южной Германии» (1933) и ее модификацией А.Лешем – «Географическое размещение хозяйства» (1940).
В. Кристаллер дал первый теоретический анализ формирования систем населенных пунктов (или «центральных мест») в рыночном пространстве. Основной постулат теории заключается в том, что размещение экономической деятельности главным образом определяется условиями спроса и предложения. Однако реальное географическое пространство крайне неоднородно, и такие факторы как рельеф, население, транспорт играют важнейшую роль, но для того, чтобы проверить влияние только спроса и предложения необходимо упростить остальные факторы и сделать допущение «при прочих равных условиях». Для теории центральных мест это упрощение заключается в том, что район рассматривается как однородная равнина с одинаково плодородными почвами, однородно распределенным населением, для которого характерны одинаковые запросы и предпочтения. Предполагается также транспортная доступность во всех направлениях. Таким образом, теория центральных мест В. Кристаллера основана на идеализированной территории, т.н. изотропной поверхности. На такой территории издержки снабжения поселения будут зависеть только от расстояния между местом производства товара и этим поселением. С увеличением издержек спрос на большинство товаров уменьшается, и поэтому очевидно, что с ростом расстояния спрос на любой товар в любом районе будет уменьшаться до тех пор, пока не будет достигнута точка, где на соответствующие товары и услуги не найдется ни один потребитель. А так как население, в свою очередь, размещено равномерно и транспортные издержки пропорциональны расстоянию, то зона сбыта любого товара будет иметь форму круга и место производства этого товара расположится в центре зоны сбыта, то есть станет «центральным местом», а все поселения, которые снабжаются из этого центра, будут «зависимыми» местами. В итоге при наличии множества городов вся территория окажется разделенной на сферы влияния. Реальный размер зоны сбыта товара полностью определяется ценой товара в центральном месте и расстоянием, на котором транспортные издержки еще терпимы сравнительно с ценой товара по сравнению с ценой такого же товара из другого центрального места.
Весь изучаемый район можно было бы разделить на ряд зон круглой формы, но здесь возникает определенная трудность: если окружности касаются друг друга, то возникают необслуженные территории, если же окружности наоборот заполняю всю территорию, то они должны пересекаться вследствие чего возникают зоны перекрытия. Поэтому наиболее эффективной формой районов сбыта является форма правильного шестиугольника. Районы в форме шестиугольника равномерно заполняют всю территорию.
За принцип построения модели размещения центральных мест В. Кристаллером был принят «поведенческий» принцип – минимум времени, сил и средств для достижения населением меньших населенных пунктов своего центрального места. Решение задачи на минимум привело к построению ортогональной (шестигранной) модели: по углам шестигранника находятся меньшие населенные пункты, а в середине – более крупный город, выполняющий функции центрального места. Зоны могут быть различными по величине в зависимости от показателей спроса.

Village – деревня, Town – город, City – крупный город, Conurbation – мегаполис
Рисунок 12 – Шестиугольники В. Кристаллера
Наиболее простые соотношения возникают, если центральное место обслуживает каждое из ближайших зависимых мест. Исходя из того, что есть 6 зависимых зон, которые непосредственно окружают центральное место, принимается предположение, что при максимальном спросе на один какой-либо товар со стороны какого-либо одного поселения, независимо от того центральное оно или зависимое, каждая зона сбыта будет содержать семь единиц спроса: шесть для зависимых мест и одно для центрального. Цифра суммарного спроса носит название «k-оценки» центрального места, и в рассмотренном случае составляет k=7.
Рассмотрим другой случай, когда, возможно, не вся клиентура зависимых территорий ориентируется на одно центральное место, например, в каждом зависимом поселении спрос может быть разделен между двумя центральными местами. В этом случае k=4, так как каждое зависимое место получает по 0,5 единицы спрос и еще одно центральное место (k=6*0,5+1).
Третий случай, когда каждое зависимое место имеет возможность разделить свой спрос между тремя центральными местами, которые одинаково доступны. В данном случае k=3, так как каждое из зависимых мест дает 1/3 единицы спроса и плюс одно центральное место (k=6*0,3+1).
Рассмотренные три системы являются основными, а множество других систем, которые можно построить, будут производными от описанных. Например, сеть с коэффициентом k=13 является производной от сети с коэффициентом k=7, так как суммарный спрос удовлетворяется одним центральным местом.
Однако товары и услуги могут быть совершенно различными: есть товары и услуги, имеющие высокий ценовой порог, а есть товары и услуги, имеющие низкий ценовой порог. Товары, имеющие высокий ценовой порог, будут продаваться в меньшем числе мест, чем товары с низким ценовым порогом. Из этого следует, что центральные места, которые предлагают товары с высоким ценовым порогом, будут находиться дальше друг от друга, чем центральные места, предлагающие товары с более низким ценовым порогом. И в результате различных сочетаний товаров и услуг, предлагаемых в различных местах, возникает иерархия центральных мест. Характер же иерархии распределения поселений по их функциональной специализации зависит не только от разнообразия предлагаемых товаров, но и от k-оценок, которые используются при моделировании иерархий поселений.
В основу своей теории В. Кристаллер положил предположение, что k-оценки определяются исходя из трех различных принципов:
- 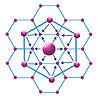 «принцип сбыта», который применяется для тех районов, где предложение товаров центральными местами должно быть максимально приближено к зависимым поселениям. Это система, где k=3 и ее производные. В данном случае возникает наибольшее возможное число центральных мест;
«принцип сбыта», который применяется для тех районов, где предложение товаров центральными местами должно быть максимально приближено к зависимым поселениям. Это система, где k=3 и ее производные. В данном случае возникает наибольшее возможное число центральных мест;
-  «транспортный принцип», который применяется в тех случаях, когда основным является учет издержек на строительство транспортной сети. Это система, где k=4 и ее производные. В данном случае наибольшее возможное число центральных мест будет располагаться на одной трассе, которая соединяет наиболее крупные города;
«транспортный принцип», который применяется в тех случаях, когда основным является учет издержек на строительство транспортной сети. Это система, где k=4 и ее производные. В данном случае наибольшее возможное число центральных мест будет располагаться на одной трассе, которая соединяет наиболее крупные города;
- 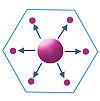 «административный принцип», который применяется для районов, где необходим четкий административный контроль над зависимыми поселениями (k=7 и ее производные).
«административный принцип», который применяется для районов, где необходим четкий административный контроль над зависимыми поселениями (k=7 и ее производные).
Основной недостаток теории центральных мест с фиксированным значением k-оценок в том, что предполагаются скачкообразные различия в спросе на товары и услуги. Минимальный размер порога при ориентации на сбыт, который можно использовать, k=3, затем будет k=9 и далее k=21. То есть, видно, что возникает очень строгая иерархия, при которой поселения данного уровня обладают одинаковым сочетанием функций, а все места более высокого ранга содержат функции центральных мест низшего ранга.
А. Лёш развил теорию центральных мест В. Кристалера. В расчётах А. Лёш использует данные о транспортных издержках и спрос как функцию цены, ставя задачу выявления оптимального размещения производственных фирм, которые при определенном спросе стремятся минимизировать транспортные издержки на единицу площади. Суть найденного им решения состоит в следующем: фирмы должны размещаться в вершинах кристаллеровской (гексагональной) решетки и каждая фирма должна обслуживать покупателей в пределах «своего» правильного шестиугольника. Тем самым А. Лёш, поддерживая концепцию идеальной формы рыночной зоны в виде шестиугольника, определил максимальный радиус рынка сбыта для различных товаров, за пределами которого реализация товаров становится невыгодной.
Модели общего равновесия (А. Лёш, У. Изард, А. Предёль)
А. Лёш дал подробное математическое описание рыночного функционирования системы производителей и потребителей, где каждая экономическая переменная привязана к определенной точке пространства. Основными элементами уравнений модели равновесия являются функции спроса и издержек. Состояние равновесия, по А. Лёшу, характеризуется следующими условиями:
- местоположение каждой фирмы обладает максимально возможными преимуществами для производителей и потребителей;
- фирмы размещаются так, что территория полностью используется;
- существует равенство цен и издержек (нет избыточного дохода);
- все рыночные зоны имеют минимальный размер (в форме шестиугольника);
- границы рыночных арен проходят по линиям безразличия (изолиниям), что, по мнению А. Лёша, обеспечивает устойчивость найденного равновесия.
Он анализирует ситуацию размещения фирм в условиях конкуренции, когда выбор местоположения определяется не только стремлением каждой фирмы к максимуму прибыли, но и увеличением числа фирм, заполняющих все рыночное пространство. Соответственно в пространственном ценообразовании отдельные фирмы должны корректировать цены с целью защиты своего рынка от проникновения других фирм.
В модели А. Лёша число уравнений совпадает с числом неизвестных. Как и Л. Вальрас, он полагал, что это не только необходимо, но и достаточно для существования равновесия. Конечно это не так, однако следует иметь в виду, что математический аппарат для доказательства существования равновесия в сложных моделях был создан значительно позже. Модели А. Лёша свойственны многие упрощающие допущения.
У. Изард облекает теорию размещения производства в более общую форму. Согласно общей теории размещения, предприятия будут стараться разместиться в такой точке пространства, где их продукция на ближайшем рынке будет обладать монополистическими преимуществами, до момента, пока не появится аналогичный продукт или продукт-заменитель. При этом на предприятии производится постоянное совершенствование и дифференциация продукта.
А. Предёль описал принцип замещения в теории общего равновесия и тем самым заложил теоретические основы для замены местоположения вследствие компенсации другим фактором. Он показал поливариантность оптимального размещения производства, отвергая идеалистические представления предшественников о наличии единственно возможного варианта оптимальной дислокации производственного объекта.
Модели пространственного взаимодействия (гравитационные модели)
Это модели взаимодействия между пространственными объектами (городами, регионами, странами) в региональном анализе и пространственном анализе экономики. В различных модификациях такие же модели используются при исследовании процессов урбанизации, экспортно-импортных взаимосвязей, миграции населения (Закон гравитации розничной торговли (У. Рейли, П. Конверс), модель демографической гравитации (Дж. Стеварт), модель демографической энергии (Г. Зипф), гравитационная модель в международной торговле (У. Изард, Ж. Тинберген). Общая черта этих моделей заключается в том, что сила взаимодействия (интенсивность потоков) в них зависит от значимости (величины) объектов и расстояния между ними. Модель называется таким образом, поскольку она несколько схожа с формулой гравитации И. Ньютона. Общая формула такова:
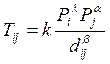
где Тij - мера притяжения объектов i и j друг к дугу;
Pi и Pj – некоторая мера значимости объекта (например, численность населения города i и города j);
dij – расстояние между ними;
k – коэффициент соответствия, зависящий от ранга события, например, если система пространственного взаимодействия достаточно хорошо определена, то значение k буден выше при рассмотрении взаимодействий между объектами в течение года, чем значение k при рассмотрении их в течение одной недели;
β – параметр, зависящий от эффективности транспортной системы между двумя объектами, например, если два объекта соединены между собой автобаном, то величина коэффициента будет ниже, чем при их взаимодействии по обычной дороге;
λ – потенциал генерации потоков. Для перемещений людей коэффициент часто зависит от суммарного уровня социального обеспечения. Например, вполне логично, что для потоков розничных товаров место, где население имеет большие доходы создает большие потоки.;
α – потенциал привлечения потоков. Зависит от вида экономической деятельности в пункте назначения. Например, центральное мест, где размещаются важные коммерческие виды деятельности, будет притягивать потоки.
Адекватность гравитационных моделей, экономическая обоснованность их применения оспаривается рядом специалистов.
А. Шеффле, используя гравитационную модель, утверждал, что промышленность развивается преимущественно в больших городах или поблизости от них. Большие города притягивают к себе промышленные предприятия, причем сила их притяжения обратно пропорциональна квадрату расстояния между ними:
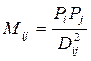 ,
,
где Мij – притяжение двух городских центров i,j;
Pi, Pj – население городов i,j;
Dij – расстояние между городами.
Локализация промышленности тем сильнее, чем больше городское население, чем меньше расстояние до рынков сбыта и чем теснее расположены крупные города. Существующие отклонения от модельного размещения приписывались сосредоточению промышленных предприятий около источников сырья и топлива.
Теория «потенциала рынка» (Ч. Харрис, Д. Рэй, А. Пред, П. Кругман)
Ч. Харрис утверждает, что при прочих равных условиях предприниматели будут стремиться размещать свое производства в местностях с хорошим доступом к рынку. Он оценил степень доступности рынка сбыта в каждом округе США, использовав для этого показатель «потенциала рынка»: взвешенную сумму покупательной способности конкретных местностей, где вес каждой местности находился в обратной зависимости от ее удаленности. Результаты этого исследования показали, что развитые промышленные регионы США, обладали высоким потенциалом рынка, поскольку в промышленном поясе (Северо-восток и средний запад США) сосредоточены значительные доли населения и производства страны, а, следовательно, регионы, входящие в этот пояс, изначально обладали наилучшим доступом к рынку. Но это наблюдение привело С. Харриса к интересному доводу – концентрация производства обладает функцией самовоспроизводства. Фирмы размещали производство в регионах с хорошим доступом к рынку, но доступ к рынку улучшался в регионах, где концентрировалось производство. Сильным местом этой модели является выявление новой причины – «потенциала рынка» или доступности к рынку сбыта, заложенной в самой концентрации производства в одном штандорте. Напомним, что до Ч. Харриса ученые экономгеографы в своих задачах оптимального размещения использовали эффект от масштаба производства, транспортные затраты и мобильность факторов производства. Слабое место ее в том, что основное это правило не срабатывает в отношении предприятий, базирующихся на немобильных факторах производства. Так, например, большой масштаб рынка сбыта нефти и газа находится далеко за пределами мест их добычи.
Д. Рэй, основываясь на модели Ч. Харриса, предложил расширенный вариант модели рыночных потенциалов с учетом влияния финансового капитала. Согласно Д. Рэю, рыночный потенциал территории является интегральным показателем, характеризующим степень экономического взаимодействия территории с рассматриваемыми региональными рынками.
А. Пред исследовал аналогичную проблему в динамике в отличие от статического подхода Ч. Харриса. Расчет модели он начинает с проекции «экспортной» выручки региона (от продаж продукции другим регионам внутри страны и за ее пределами), после чего использует оценочный коэффициент доли дохода, затрачиваемого внутри региона, для определения на его базе мультипликатора. Он полагает, что объем экспортной базы и доля дохода, затрачиваемого внутри региона должны быть возрастающими функциями размеров региональной экономики. Это означает, что если экономика региона достигает достаточно больших масштабов, то она может вступить в период кумулятивного роста. Большой объем спроса на внутрирегиональном рынке может сделать выгодным местное производство товаров, ранее не производившихся в данном регионе, что увеличит мультипликатор экспортной базы региона, приводя к дальнейшему росту дохода, который вызовет дополнительное увеличение производства, и т.д. Безусловно, эта модель работает на уровне страны, но внутри страны на уровне региона она может давать сбои из-за передачи части региональных доходов центральному правительству.
В основе теории Ч. Харриса и А. Преда лежит имплицитное предположение о наличии значительных эффектов масштаба на уровне отдельного предприятия, поскольку в случае их отсутствия у производителей не будет причин концентрировать свою деятельность в одном месте, они скорее будут снабжать потребителей своей продукцией с нескольких заводов, тем самым, будут подорваны выводы Харриса. А сужение регионального рынка не будет стимулировать расширение номенклатуры товаров, производимых в этом регионе, а это уже подрывает выводы А. Преда. Другими словами, эффект масштаба - центральное звено этих теорий. Следовательно, возрастающий эффект масштаба на уровне предприятий и расширение регионального рынка выступают главными факторами образования региональной агломерации, а она, в свою очередь, становится главной причиной неравномерного экономического развития регионов и всей экономики страны. Основной недостаток этих моделей – они не открывают возможностей поиска и путей сближения межстрановых и межрегиональных различий экономического развития.
П. Кругман попытался формализовать теории данных авторов в одной модели. Его модель это экономическая система, состоящая из двух регионов (хотя модель позволяет расширение ее до большего числа регионов) и двух отраслей: совершенно конкурентного сельского хозяйства и несовершенно конкурентной (по Дикситу-Стиглицу) промышленности. Товар аграрной отрасли производится фермерами, которые отличаются абсолютной немобильностью, напротив, промышленные рабочие обладают абсолютной мобильностью и могут перемещаться в тот регион, где предлагают более высокую заработной плату. Кроме того, издержки промышленного товара (но не аграрного) включают в себя айсберговые транспортные затраты, где часть товаров просто «тает» в пути, т.е. транспортные издержки, включаются в цены в достигнутых местах назначения товаров.
Эффект масштаба находится исключительно на уровне фирм, центростремительные силы, заставляющие промышленность концентрироваться в одном регионе, возникают в результате трехстороннего взаимодействия эффекта масштаба, транспортных издержек и мобильности факторов. В общих чертах: фирмы стремятся сосредотачивать производства (из-за эффекта масштаба) вблизи рынков сбыта и поставщиков (из-за транспортных издержек), в то время как доступ к рынкам сбыта и поставщикам лучше всего там, где сосредоточены другие фирмы (из-за эффекта объема рынка). Сочетание этих эффектов создает агломерацию, несмотря на то, что ей противодействует центробежная сила, генерируемая немобильностью аграрного сектора и побуждающая промышленные фирмы перемещаться в регион с меньшим количеством местных конкурентов.
Date: 2015-05-09; view: 6779; Нарушение авторских прав