Краткая теория. Планетарная модель атома, предложенная Резерфордом, – это попытка применения классических представлений о движении тел к явлениям атомных масштабов

Планетарная модель атома, предложенная Резерфордом, – это попытка применения классических представлений о движении тел к явлениям атомных масштабов. Эта попытка оказалась несостоятельной. Классический атом неустойчив. Электроны, движущиеся по орбите с ускорением, должны неизбежно упасть на ядро, растратив всю энергию на излучение электромагнитных волн (рис. 3.1.).

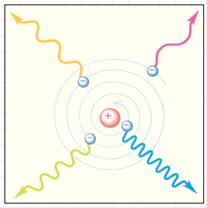
Рисунок 3.1.

Неустойчивость классического атома.

Следующий шаг в развитии представлений об устройстве атома сделал в 1913 году выдающийся датский физик Н. Бор. Проанализировав всю совокупность опытных фактов, Бор пришел к выводу, что при описании поведения атомных систем следует отказаться от многих представлений классической физики. Он сформулировал постулаты, которым должна удовлетворять новая теория о строении атомов.

Первый постулат Бора (постулат стационарных состояний) гласит: атомная система может находится только в особых стационарных или квантовых состояниях, каждому из которых соответствует определенная энергия E _n. В стационарных состояниях атом не излучает.

Этот постулат находится в явном противоречии с классической механикой, согласно которой энергия движущегося электрона может быть любой. Он находится в противоречии и с электродинамикой, так как допускает возможность ускоренного движения электронов без излучения электромагнитных волн. Согласно первому постулату Бора, атом характеризуется системой энергетических уровней, каждый из которых соответствует определенному стационарному состоянию (рис. 3.2.). Механическая энергия электрона, движущегося по замкнутой траектории вокруг положительно заряженного ядра, отрицательна. Поэтому всем стационарным состояниям соответствуют значения энергии E_n < 0. При E_n ≥ 0 электрон удаляется от ядра (ионизация). Величина |E₁| называется энергией ионизации. Состояние с энергией E₁ называется основным состоянием атома.

Рисунок 3.2.

Энергетические уровни атома и условное изображение процессов поглощения и испускания фотонов.

Второй постулат Бора (правило частот) формулируется следующим образом: при переходе атома из одного стационарного состояния с энергией E _n в другое стационарное состояние с энергией E _m излучается или поглощается квант, энергия которого равна разности энергий стационарных состояний:

h ν_nm = E _n – E _m

где h – постоянная Планка. Отсюда можно выразить частоту излучения:

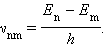
Второй постулат Бора также противоречит электродинамике Максвелла, так как частота излучения определяется только изменением энергии атома и никак не зависит от характера движения электрона.

Теория Бора не отвергла полностью законы классической физики при описании поведения атомных систем. В ней сохранились представления об орбитальном движении электронов в кулоновском поле ядра. Классическая ядерная модель атома Резерфорда была дополнена в теории Бора идеей о квантовании электронных орбит. Поэтому теорию Бора иногда называют полуклассической.

Простейший из атомов, атом водорода явился своеобразным тест-объектом для теории Бора. Ко времени создания теории Бора атом водорода был хорошо изучен экспериментально. Он содержит единственный электрон. Ядром атома является протон – положительно заряженная частица, заряд которой равен по модулю заряду электрона, а масса в 1836 раз превышает массу электрона. Еще в начале XIX века были открыты дискретные спектральные линии в излучении атома водорода в видимой области (так называемый линейчатый спектр). Впоследствии закономерности, которым подчиняются длины волн (или частоты) линейчатого спектра, были хорошо изучены количественно (И. Бальмер, 1885 г.). Совокупность спектральных линий атома водорода в видимой части спектра была названа серией Бальмера. Позже аналогичные серии спектральных линий были обнаружены в ультрафиолетовой и инфракрасной частях спектра. В 1890 году И. Ридберг получил эмпирическую формулу для частот спектральных линий:

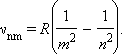
Для серии Бальмера m = 2, n = 3, 4, 5,.... Для ультрафиолетовой серии (серия Лаймана) m = 1, n = 2, 3, 4,.... Постоянная R в этой формуле называется постоянной Ридберга. Ее численное значение R = 3,29·10¹⁵ Гц. До Бора механизм возникновения линейчатых спектров и смысл целых чисел, входящих в формулы спектральных линий водорода (и ряда других атомов), оставались непонятными.

Постулаты Бора определили направление развития новой науки – квантовой физики атома. Но они не содержали рецепта определения стационарных состояний (орбит) и соответствующих им значений энергии E_n.

Правило квантования, приводящее к правильным, согласующимся с опытом значениям энергий стационарных состояний атома водорода, было угадано Бором. Бор предположил, что момент импульса электрона, вращающегося вокруг ядра, может принимать только дискретные значения, кратные постоянной Планка. Для круговых орбит правило квантования Бора записывается в виде

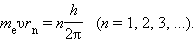
Здесь m_e – масса электрона, υ – его скорость, r_n – радиус стационарной круговой орбиты. Правило квантования Бора позволяет вычислить радиусы стационарных орбит электрона в атоме водорода и определить значения энергий. Скорость электрона, вращающегося по круговой орбите некоторого радиуса r в кулоновском поле ядра, как следует из второго закона Ньютона, определяется соотношением

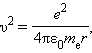
где e – элементарный заряд, ε₀ – электрическая постоянная. Скорость электрона υ и радиус стационарной орбиты r_n связаны правилом квантования Бора. Отсюда следует, что радиусы стационарных круговых орбит определяются выражением

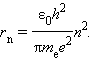
Самой близкой к ядру орбите соответствует значение n = 1. Радиус первой орбиты, который называется боровским радиусом, равен

Радиусы последующих орбит возрастают пропорционально n².

Полная механическая энергия E системы из атомного ядра и электрона, обращающегося по стационарной круговой орбите радиусом r_n, равна

Следует отметить, что E_p < 0, так как между электроном и ядром действуют силы притяжения. Подставляя в эту формулу выражения для υ² и r_n, получим:

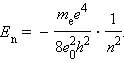
Целое число n = 1, 2, 3,... называется в квантовой физике атома главным квантовым числом.

Согласно второму постулату Бора, при переходе электрона с одной стационарной орбиты с энергией E_n на другую стационарную орбиту с энергией E_m < E_n атом испускает квант света, частота ν_nm которого равна ΔE_nm / h:

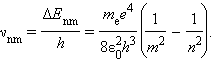
Эта формула в точности совпадает с эмпирической формулой Ридберга для спектральных серий атома водорода, если положить постоянную R равной

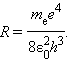
Подстановка числовых значений m_e, e, ε₀ и h в эту формулу дает результат

R = 3,29·10¹⁵ Гц,

который очень хорошо согласуется с эмпирическим значением R. Рис. 3.3. иллюстрирует образование спектральных серий в излучении атома водорода при переходе электрона с высоких стационарных орбит на более низкие.

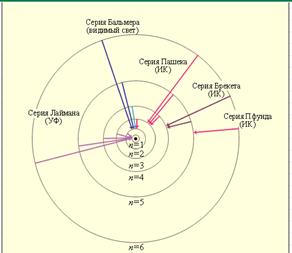
Рисунок 3.3.

Стационарные орбиты атома водорода и образование спектральных серий.

На рис. 3.4. изображена диаграмма энергетических уровней атома водорода и указаны переходы, соответствующие различным спектральным сериям.

Рисунок 3.4.

Диаграмма энергетических уровней атома водорода. Показаны переходы, соответствующие различным спектральным сериям. Для первых пяти линий серии Бальмера в видимой части спектра указаны длины волн.

Прекрасное согласие боровской теории атома водорода с экспериментом служило веским аргументом в пользу ее справедливости. Однако попытки применить эту теорию к более сложным атомам не увенчались успехом. Бор не смог дать физическую интерпретацию правилу квантования. Это было сделано десятилетием позже де Бройлем на основе представлений о волновых свойствах частиц. Де Бройль предложил, что каждая орбита в атоме водорода соответствует волне, распространяющейся по окружности около ядра атома. Стационарная орбита возникает в том случае, когда волна непрерывно повторяет себя после каждого оборота вокруг ядра. Другими словами, стационарная орбита соответствует круговой стоячей волне де Бройля на длине орбиты (рис. 3.5.). Это явление очень похоже на стационарную картину стоячих волн в струне с закрепленными концами.

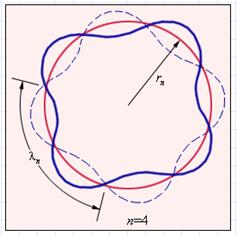
Рисунок 3.5.

Иллюстрация идеи де Бройля возникновения стоячих волн на стационарной орбите для случая n = 4.

В стационарном квантовом состоянии атома водорода на длине орбиты должно укладываться по идее де Бройля целое число длин волн λ, т. е.

n λ_n = 2π r _n.

Подставляя в это соотношение длину волны де Бройля λ = h / p, где p = m_eυ – импульс электрона, получим:

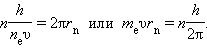
Таким образом, боровское правило квантования связано с волновыми свойствами электронов.

Успехи теории Бора в объяснении спектральных закономерностей в изучении атома водорода были поразительны. Стало ясно, что атомы – это квантовые системы. Энергетические уровни стационарных состояний атомов дискретны. Почти одновременно с созданием теории Бора было получено прямое экспериментальное доказательство существования стационарных состояний атома и квантования энергии. Дискретность энергетических состояний атома была продемонстрирована в опыте Д. Франка и Г. Герца (1913 г.), в котором исследовалось столкновение электронов с атомами ртути. Оказалось, что если энергия электронов меньше 4,9 эВ, то их столкновение с атомами ртути происходит по закону абсолютно упругого удара. Если же энергия электронов равна 4,9 эВ, то столкновение с атомами ртути приобретает характер неупругого удара, т. е. в результате столкновения с неподвижными атомами ртути электроны полностью теряют свою кинетическую энергию. Это означает, то атомы ртути поглощают энергию электрона и переходят из основного состояния в первое возбужденное состояние,

E₂ – E₁ = 4,9 эВ.

Согласно боровской концепции, при обратном самопроизвольном переходе атома ртуть должна испускать кванты с частотой

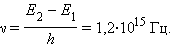
Спектральная линия с такой частотой действительно была обнаружена в ультрафиолетовой части спектра в излучении атомов ртути.

Представление о дискретных состояниях противоречит классической физике. Поэтому возник вопрос, не опровергает ли квантовая теория законы классической физики. Квантовая физика не отменила фундаментальных классических законов сохранения энергии, импульса, электрического разряда и т. д. Согласно сформулированному Н. Бором принципу соответствия, квантовая физика включает в себя законы классической физики, и при определенных условиях можно обнаружить плавный переход от квантовых представлений к классическим. Это можно видеть на примере энергетического спектра атома водорода (рис. 3.6). При больших квантовых числах n >> 1 дискретные уровни постепенно сближаются, и возникает плавный переход в область непрерывного спектра, характерного для классической физики.

Половинчатая, полуклассическая теория Бора явилась важным этапом в развитии квантовых представлений, введение которых в физику требовало кардинальной перестройки механики и электродинамики. Такая перестройка была осуществлена в 20-е – 30-е годы XX века.

Представление Бора об определенных орбитах, по которым движутся электроны в атоме, оказалось весьма условным. На самом деле движение электрона в атоме очень мало похоже на движение планет или спутников. Физический смысл имеет только вероятность обнаружить электрон в том или ином месте, описываемая квадратом модуля волновой функции | Ψ|². Волновая функция Ψ является решением основного уравнения квантовой механики – уравнения Шредингера (см. модель). Оказалось, что состояние электрона в атоме характеризуется целым набором квантовых чисел. Главное квантовое число n определяет квантование энергии атома. Для квантования момента импульса вводится так называемое орбитальное квантовое число l. Проекция момента импульса на любое выделенное в пространстве направление (например, направление вектора магнитного поля) также принимает дискретный ряд значений. Для квантования проекции момента импульса вводится магнитное квантовое число m. Квантовые числа n, l, m связаны определенными правилами квантования. Например, орбитальное квантовое число l может принимать целочисленные значения от 0 до (n – 1). Магнитное квантовое число m может принимать любые целочисленные значения в интервале ± l. Таким образом, каждому значению главного квантового числа n, определяющему энергетическое состояние атома, соответствует целый ряд комбинаций квантовых чисел l и m. Каждой такой комбинации соответствует определенное распределение вероятности | Ψ|² обнаружения электрона в различных точках пространства («электронное облако»).

Состояния, в которых орбитальное квантовое число l = 0, описываются сферически симметричными распределениями вероятности. Они называются s -состояниями (1s, 2s,..., ns,...). При значениях l > 0 сферическая симметрия электронного облака нарушается. Состояния с l = 1 называются p -состояниями, с l = 2 – D -состояниями и т. д.

На рис. 3.6 изображены кривые распределения вероятности ρ(r) = 4πr²|Ψ|² обнаружения электрона в атоме водорода на различных расстояниях от ядра в состояниях 1s и 2s.

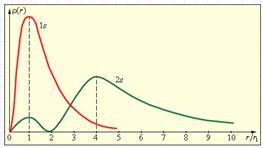
Рисунок 3.6.

Распределение вероятности обнаружения электрона в атоме водорода в состояниях 1s и 2s. r₁ = 5,29·10^–11 м – радиус первой боровской орбиты.

Как видно из рис. 3.6, электрон в состоянии 1 s (основное состояние атома водорода) может быть обнаружен на различных расстояниях от ядра. С наибольшей вероятностью его можно обнаружить на расстоянии, равном радиусу r₁ первой боровской орбиты. Вероятность обнаружения электрона в состоянии 2s максимальна на расстоянии r = 4r₁ от ядра. В обоих случаях атом водорода можно представить в виде сферически симметричного электронного облака, в центре которого находится ядро.

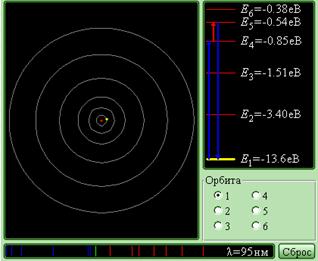
Модель. Постулаты Бора.

Компьютерная модель является иллюстрацией постулатов Бора в применении к круговым орбитам атома водорода. Модель позволяет исследовать переходы между несколькими низшими орбитами атома водорода, сопровождающиеся излучением или поглощением фотона определенной частоты или длины волны. Указываются длины волн соответствующих переходов. Некоторые спектральные линии, расположенные в диапазоне видимого света, изображены цветными полосками. Это линии соответствуют переходам на вторую стационарную орбиту с более удаленных орбит (так называемая серия Бальмера). Ультрафиолетовые линии условно изображены синими полосками, линии инфракрасной части спектра – красными полосками. В правом верхнем углу экрана изображена схема энергетических уровней атома водорода, на которой стрелками изображаются переходы между уровнями энергии, то есть переходы между стационарными орбитами.

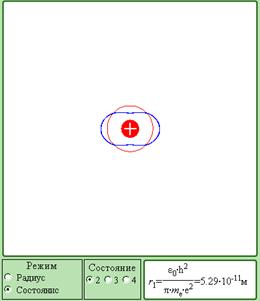
Модель. Квантования электронных орбит

Компьютерная модель является качественной иллюстрацией идеи де Бройля возникновения стоячих волн на стационарных орбитах.

Модель позволяет, плавно изменяя радиус, выбирать стационарные орбиты, на длине которых укладывается целое число длин волн де Бройля и образуется стоячая волна.

Компьютерная модель на примере орбит с квантовыми числами n = 2, 3 и 4 иллюстрирует закономерность, которой подчиняются радиусы стационарных круговых орбит в атоме водорода. Согласно теории Бора

r_n = n²r₁,

где r₁ = 5,29·10^–11 м – радиус первой боровской орбиты.

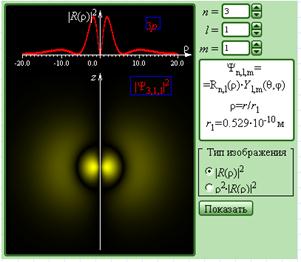
Модель. Атом водорода.

Состояние частиц в квантовой физике описывается с помощью волновых функций Ψ (пси-функций). Квадрат модуля волновой функции |Ψ|² пропорционален вероятности нахождения частицы в данной точке пространства. Таким образом, принципиальное отличие квантовомеханического способа описания системы от классического заключается в вероятностном подходе. С помощью пси-функции можно найти только вероятность обнаружения частицы в некоторой области пространства.

Отыскание конкретного вида волновых функций достигается в квантовомеханических задачах путем решения основного уравнения квантовой механики – уравнения Шредингера (1926 г.), которое является математическим выражением фундаментальных свойств микросистем. Уравнение Шредингера позволяет отыскивать вид пси-функции частицы, движущейся в заданных силовых полях. Оказывается, что уравнение Шредингера имеет решение только при определенных значениях полной энергии системы, которые называются собственными значениями. Таким образом, уравнение Шредингера позволяет получить правила квантования полной энергии замкнутой системы.

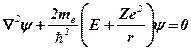
r – расстояние электрона от ядра

Ze – заряд ядра

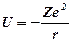- потенциальная энергия электрона

т_е – масса электрона

ћ – постоянная Планка

Е – полная энергия

Так как кулоновское поле ядра атома водорода является сферически симметричным, решение уравнения Шредингера удобно искать в сферической системе координат (r, θ, φ).

Общее решение уравнения Шредингера для атома водорода имеет вид

Ψ_{n, l, m}(r, θ, φ) = R _{n, l}(r) Y _{l, m}(θ, φ).

Волновая функция Ψ зависит от трех целых чисел: n, l и m, которые называются квантовыми числами. Главное квантовое число n определяет квантование энергетических уровней. Оно может принимать значения n = 1, 2, 3,.... Орбитальное квантовое число l определяет квантование момента импульса атома водорода. Оно может принимать целочисленные значения в пределах от 0 до n – 1. Состояния с l = 0 принято называть S -состояниями, c l = 1 – P -состояниями, с l = 2 – D -состояниями и т. д. В S -состояниях момент импульса атома водорода равен нулю. Квантовое число m определяет квантование в единицах постоянной Планка ħ = h / 2π проекции момента импульса на выделенное направление в пространстве. Оно называется магнитным квантовым числом и может принимать значения m = 0, ±1, ±2,..., ±l. Таким образом, атом может находиться в нескольких различных состояниях с одним и тем же значением полной энергии. В возбужденных состояниях (т. е. при n > 0) полная энергия атома водорода равна

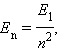
где E₁ – энергия атома в основном 1S состоянии, равная

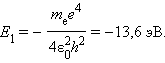
Боровских орбит в атоме в действительности не существует. В каждом состоянии может быть указано только распределение вероятности нахождения электрона на различных расстояниях от ядра, которое называют электронным облаком. Наряду с функцией |Ψ|² графически удобно изображать функцию r²|Ψ|², которая пропорциональна вероятности нахождения электрона в сферическом слое радиуса r единичной толщины.

Компьютерная модель предназначена для иллюстрации строгого решения задачи о состояниях атома водорода при значениях главного квантового числа n = 1, 2 и 3. При графическом изображении радиальных распределений вероятности удобно в качестве переменной величины использовать безразмерное отношение ρ = r / r₁, где r₁ = 5,29·10^–11 м – радиус первой боровской орбиты.

В верхней части экрана высвечиваются радиальные распределения |R(ρ)|² или ρ²|R(ρ)|², где функция R является радиальной частью волновой функции Ψ. ρ²|R(ρ)|² плотность вероятности нахождения электрона на расстоянии r от ядра. В нижней части экрана воспроизводится для заданных значений квантовых чисел n, l, m пространственное распределение вероятности |Ψ(r, θ, φ)|² (электронное облако).

Изменяя значения n, l, m, следует кликнуть мышью на клавишу «показать» и пронаблюдать за изменениями радиального распределения вероятности (волновой функции) – электронного облака.

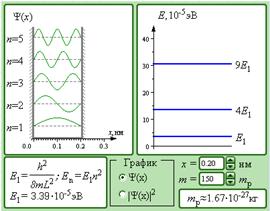
Модель. Частица в потенциальной яме.

Стоячие волны де Бройля, образующиеся при движении частицы в потенциальной яме, это и есть волновые или пси-функции, с помощью которых квантовая механика описывает стационарные состояния микрообъектов. Квадрат модуля |Ψ|² волновой функции определяется как вероятность нахождения частицы в различных точках пространства.

В компьютерной модели можно изменять ширину L потенциальной ямы, а также массу m запертой в ней частицы. В левом окне высвечиваются графические изображения волновых функций Ψ( x ) или квадратов их модулей |Ψ|² для нескольких стационарных состояний ( n = 1–5). В правом окне изображается энергетический спектр частицы, то есть спектр возможных значений ее энергии. Обратите внимание, что энергетические уровни опускаются при увеличении ширины L потенциальной ямы и массы m запертой в ней частицы.

В компьютерной модели масса частицы выражается в массах протона m_p = 1,67·10^–27 кг. Следовательно, моделируются состояния сравнительно тяжелых частиц (ядер тяжелых атомов), оказавшихся в потенциальной яме с шириной порядка размеров атомов.

Date: 2015-05-09; view: 2566; Нарушение авторских прав