Поперечный характер электромагнитных волн

В предыдущих параграфах мы рассмотрели основные свойства гармонических волн, вытекающих из очевидных и общих представлений о зависимости колебаний их векторов электрического и магнитного полей от времени и расстояния, пройденного волной от источника до точки наблюдения. Обоснуем эти соображения прямым решением системы уравнений Максвелла вместе с материальными уравнениями (1.1a) относительно четвёрки векторов 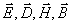, определяющих электромагнитную волну. Рассмотрим плоскую гармоническую электромагнитную волну круговой частоты 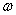, распространяющуюся вдоль оси 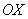в однородной, непроводящей среде с (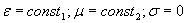). Для такой волны в соответствии с её определением (1.3) вектора 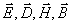не зависят от координат y и z, т.к. амплитуда их колебаний имеет постоянное значение для любой точки наблюдения, а фаза не изменяется в любой плоскости, параллельной плоскости (рис.1.1). Таким образом, вектора 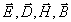зависят только от времени 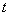и координаты 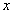. Исключая равные нулю частные производные компонент этих векторов по переменным 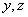получим из (1.1b) определяющие каждую из декартовых компонент 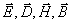при 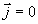следующие уравнения:

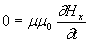;(1.4a)

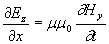;(1.4b)

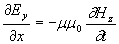;(1.4c)

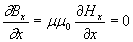;(1.4d)

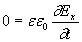;(1.4e)

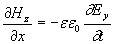;(1.4f)

;(1.4g)

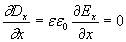.(1.4h)

Отсюда следует, что одним из решений системы (1.4) являются электростатическое и магнитостатическое поля, поскольку проекции на ось 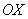любого из векторов электромагнитного поля 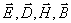имеют равные нулю частные производные по координате 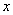и времени .

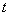Тогда, очевидно,

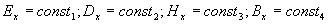
представляют постоянные электрическое и магнитное поля, ориентированные вдоль направления распространения плоской волны, накладывающиеся на меняющееся во времени электромагнитное поле волны и не зависящие от него. По этой причине без ограничения общности можно полагать их равными нулю, т.е.:

.

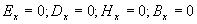Следовательно, отличными от нуля компонентами плоской электромагнитной гармонической волны, распространяющейся вдоль оси 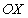, являются: ,

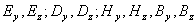перпендикулярные .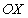

Отсюда следует важный вывод, что вектора напряжённости электрического и магнитного полей плоской электромагнитной гармонической волны колеблются в плоскости, перпендикулярной направлению распространения волны. Волны, обладающие таким свойством, называются поперечными. Следовательно, электромагнитные волны являются поперечными волнами (рис.1.3).

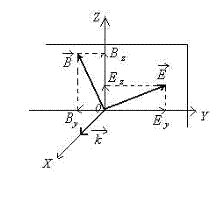Рис. 1.3.

Поляризация колебаний плоской гармонической электромагнитной волны.

Второй важный вывод, который можно сделать из системы уравнений (1.4), состоит в том, что эта система уравнений представляет собой две независимые системы уравнений:

первая состоит из уравнений (1.4b), (1.4g), определяющих :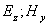

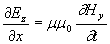;(1.5a)

;(1.5b)

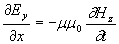;(1.6a)

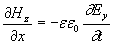.(1.6b)

вторая состоит из уравнений (1.4c), (1.4f), определяющих :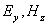

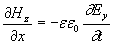
Существование двух независимых друг от друга систем дифференциальных уравнений (1.5) и (1.6) позволяет рассматривать плоскую гармоническую волну с произвольной ориентацией вектора напряженности электрического поля электромагнитной волны в плоскости волнового фронта в виде суммы двух независимых плоских гармонических волн той же частоты, что и исходная, направления колебаний векторов напряженности электрического и магнитного полей взаимно перпендикулярны. Эта особенность векторного характера колебаний электромагнитной волны следует из законов электромагнетизма, составляющих физическую основу уравнений Максвелла. Действительно, пусть первоначально было переменное во времени электрическое поле 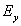с направлением колебаний вектора напряженности электрического поля вдоль оси 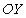, то возникнет ток смещения, благодаря которому генерируется магнитное поле 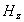с колебаниями вдоль оси 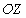(рис.1.4a). Магнитное поле 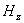создаёт вихревое поле 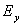. При этом электромагнитное поле с компонентами 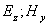не возникает. Аналогично рассуждая, можно рассмотреть взаимное превращение первоначально созданного электрического поля 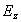в магнитное поле 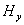(рис.1.4b). При этом электромагнитная волна с электрическим и магнитным полями 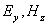не возникает.

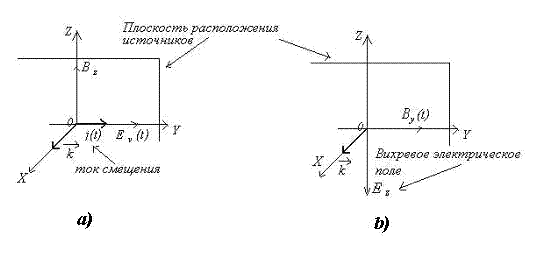
Рис. 1.4.

Возможность представления произвольной плоской гармонической электромагнитной волны в виде суммы двух независимых волн с перпендикулярно колеблющимися в одной фазе по отношению друг к другу парами векторов напряженности электрического и магнитного полей определяет свойство поляризации электромагнитной волны.Поляризация электромагнитной волны определяется направлением колебаний вектора напряженности электрического поля. В рассматриваемом случае плоская волна, распространяющаяся вдоль оси 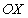с произвольным направлением колебаний вектора напряженности электрического поля в плоскости 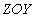, может быть представлена в виде суммы двух электромагнитных волн, поляризованных в двух взаимно ортогональных направлениях, которые с учётом того, что ось 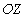задаёт вертикальное направление по отношению к плоскости 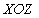, отождествляемой с плоскостью горизонта, условно могут быть названы:

а) волны с горизонтальной поляризацией, определяемые колебаниями векторов ;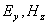

б) волны с вертикальной поляризацией, определяемые колебаниями векторов .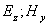

На рис.1.5 изображены направления колебаний соответствующие горизонтальной и вертикальной поляризации электромагнитных волн, распространяющихся со скоростью 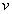вдоль оси OX. Из этих рисунков следует, что вектора напряженности электрического 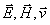и магнитного 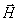полей, а также скорости волны 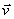образуют правую тройку векторов. Направление колебаний векторов 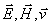электромагнитной волны вертикальной поляризации, изображённой на рис.1.5a, получается после поворота тройки векторов рис.1.5a на 90⁰ вокруг оси OX. Направление колебаний векторов 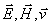электромагнитной волны горизонтальной поляризации, изображённой на рис.1.5b, получается после поворота тройки векторов рис.1.5a на 180⁰ вокруг оси OZ.

.

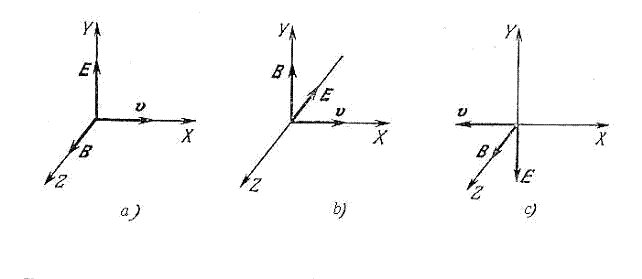
Рис. 1.5

Волны с линейной поляризацией являются простейшими поляризованными волнами. Более сложным видом поляризации волн является круговая поляризация. В плоской электромагнитной волне круговой поляризации вектора напряженности электрического и магнитного поля равномерно вращаются вокруг своего направления распространения, образуя в каждый момент времени вместе с волновым вектором правую тройку векторов. Вращение указанных выше векторов может происходить как против часовой стрелки, так и по часовой стрелке, если смотреть с конца волнового вектора. Волны круговой поляризации волны с вращением векторов поля по часовой стрелке и против часовой стрелки являются волнами с ортогональными поляризациями. В соответствии с этим говорят о волнах, поляризованных по правому и левому кругу.

Рис. 1.6.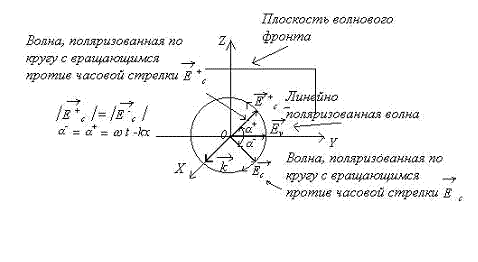

Волновое уравнение. Связь амплитуд и фаз векторов напряженности электрического и магнитного полей плоской электромагнитной волны. Ввиду независимости колебаний волн с ортогональными поляризациями дальнейший анализ свойств распространения плоской электромагнитной сосредоточим на изучении свойств волны одной какой-нибудь поляризации, например, горизонтальной с компонентами электрического и магнитного поля, соответственно равными 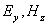. Убедимся, что компоненты электромагнитного поля 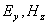удовлетворяют волновому уравнению. Для этой цели продифференцируем уравнение (1.6a) по 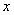, а уравнение (1.6b) по 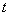и после исключения смешанной производной получим:

;

Если подставить значения электрической и магнитной 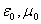постоянных, то получим следующую величину их произведения: 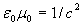,(1.7)

где 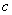- скорость света в вакууме.

В силу соотношения (1.7) для определения E y получаем волновое уравнение:

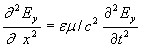;(1.8a)

Аналогично получается волновое уравнение для 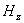, а также для компонент плоской электромагнитной волны вертикальной поляризации 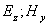, определяемых (1.5).

Уравнение (1.8a) называется волновым, в частности, из-за того, что его решением является³ плоская электромагнитная волна, определённая выше соотношением (1.3) для колебаний вектора напряжённости электрического поля: 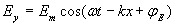,(1.9a)

где волновое число 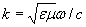,(1.9b)

- зависящее в общем случае от относительных диэлектрических и магнитных 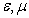проницаемостей среды распространения электромагнитной волны.

Аналогичным образом можно убедиться, что решением волнового уравнения являются колебания вектора напряжённости магнитного поля 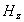в виде плоской волны:

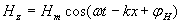;(1.9c)

В выражениях (1.9) 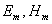- амплитуды электрической и магнитной компонент плоской волны; 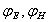- начальные фазы колебаний векторов напряжённостей электрического и магнитного полей; 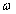- частота волны.

Между амплитудами и фазами колебаний электрической и магнитной компонент электромагнитной волны имеются соотношения, следующие из системы уравнений (1.6) для горизонтальной поляризации 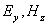и системы уравнений (1.5) для волны вертикальной поляризации 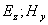. Подставим выражения (1.9) в (1.6):

;(1.10a) 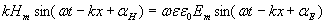.(1.10b)

Очевидно, для того, чтобы эти соотношения были справедливы для любых 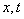начальные фазы электрической и магнитной компоненты электромагнитной волны должны быть равными: 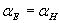.(1.11a)

Если это соотношение имеет место, то из (1.10) следуют два равенства, связывающие амплитуды электрической и магнитной компоненты :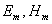

;

.

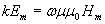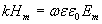Перемножая эти равенства, получаем соотношение между амплитудами электрической и магнитной компонент плоской электромагнитной волны:

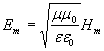.(1.11b)

Размерность коэффициента пропорциональности в соотношении (1.11b) между амплитудами электрической и магнитной компонент плоской волны, совпадает с размерностью ' сопротивления '. Действительно: размерность величины , обозначаемая символом - 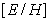, равна: .

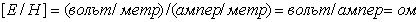По этой причине величина

(1.12)

называется волновым сопротивлением среды распространения электромагнитных волн.

Для волны, распространяющейся в вакууме (в сухом воздухе) :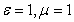

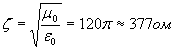(1.13)

Величина 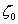называется волновым сопротивлением вакуума.

Для вертикальной поляризации плоской волны с компонентами электрического и магнитного полей 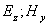имеют место аналогичные соотношения (1.11), связывающие их амплитуды и фазы их колебаний.

Определим единичный вектор 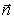в направлении распространения волны, и одновременно перпендикулярный плоскости её волнового фронта.

Рассматривая (1.11) для двух возможных поляризаций плоской электромагнитной волны можно сделать вывод, что тройка векторов, состоящая из 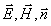является правой. Это обозначает, что при наблюдении векторов 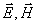с конца вектора 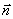вектор 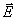может быть совмещен с вектором 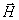вращением против часовой стрелки в сторону меньшего угла.

С помощью вектора 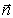и выражений (1.12) могут быть получены соотношения для плоской гармонической электромагнитной волны, связывающее вектора 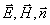друг с другом с помощью векторного произведения (рис.1.3):

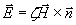.(1.12a)

Верным является и обратное соотношение:

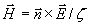.(1.12b)

И кроме того,

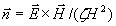.(1.12c)

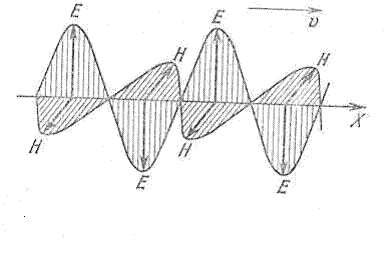Рис. 1.8.

На рис.1.8 изображена "мгновенная фотография" колебаний векторов напряжённости плоской электромагнитной волны, распространяющейся вдоль оси .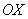

В дальнейшем при изучении свойств электромагнитных волн с вектором 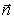связывается волновой вектор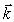

,

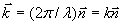модуль которого определяется волновым числом (длиной волны), а направление совпадает с направлением распространения электромагнитной волны. В соответствии со сказанным выше тройка векторов, состоящая из 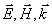, является правой.

Date: 2015-05-09; view: 1078; Нарушение авторских прав