Фазовая и групповая скорости электромагнитной волны

Электромагнитная волна, колебания векторов электрического и магнитного поля которой задаются уравнениями (1.9), представляет собой физический процесс, протекающий с конечной скоростью, равной скорости света 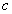в среде, где она распространяется. Чтобы в этом убедиться рассмотрим волновое уравнение (1.8), в котором обозначим

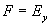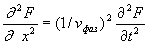: ,(1.13a)

где имеющий размерность скорости коэффициент

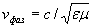,(1.13b)

определяет, как будет показано ниже, фазовую скорость распространения электромагнитной волны, зависящую от значений диэлектрической и магнитной проницаемостей среды её распространения. Можно показать, что решением волнового уравнения (1.13a) является произвольная дважды дифференцируемая функция 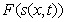, например, изображённая на рис.1.9a, зависящая от линейной комбинации координаты и времени

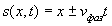.(1.13c)

Знак 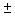в выражении (1.13c) означает, что решением уравнения (1.13a)

является как функция 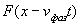, так и функция .

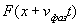Рис. 1.9.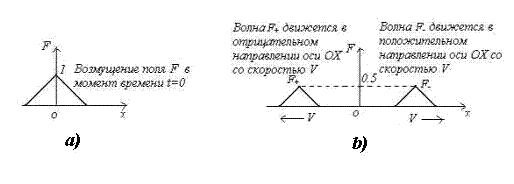

Функция 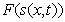, изображённой на рис. 1.9a, при изменении времени перемещается вдоль оси (рис.1.9b) в соответствии с нашими интуитивными представлениями о перемещении гребня волны. Это свойство решения уравнения (1.13b) явилось основанием назвать его волновым (Д' Аламбер).

Аргумент рассматриваемой функции 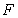, называется, как и в частном случае плоской гармонической волны, полной фазой :

.

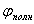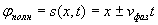Множество точек в пространстве, в которых фаза волны имеет постоянное значение, называется волновым фронтом волны. Для рассматриваемого случая плоской волны (1.9) волновым фронтом является любая плоскость, параллельная плоскости .

Физический смысл полной фазы 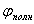состоит в том, что с её помощью можно определить перемещение волнового фронта волны из исходной точки 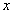за время, равное .

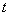Решение волнового уравнения (1.13a) в виде плоской гармонической волны (1.9), очевидно, является частным случаем рассмотренного выше, когда в качестве произвольной функции 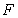выбрана функция косинуса. Выражение для полной фазы плоской гармонической волны 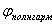получается из выражения для полной фазы 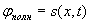произвольной волны при умножении её величины, измеряемой в единицах длины (метрах), на волновое число 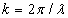для пересчёта в радианы:

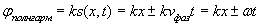, Где 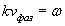.(1.13d)

Очевидно, полная фаза для рассматриваемой волны имеет постоянное значение 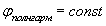на любой плоскости, параллельной плоскости :

.

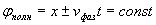Это соотношение можно рассматривать, как уравнение для определения изменения положения выбранной плоскости постоянной фазы 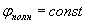волны во времени:

.

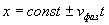С помощью дифференцирования найдём скорость перемещения плоскости постоянной фазы, называемой фазовой скоростью :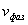

,

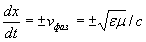совпадающей с (1.13b).

Отсюда следует, что любая плоскость равной фазы для волны, представляемой функцией 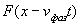, перемещается со скоростью 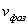в положительном направлении оси 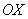. Плоскость равной фазы для волны 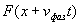, перемещается со скоростью 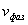в отрицательном направлении оси

.

Рис. 1.10.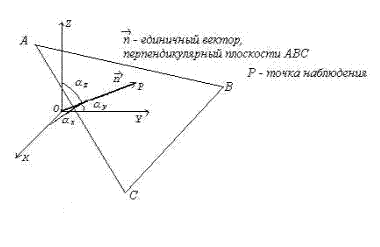

При рассмотрении свойств плоских электромагнитных волн мы ограничились случаем распространения волн вдоль оси . Это не ограничивает строгость полученных результатов, поскольку с помощью поворота (вращения) осей используемой системы координат можно совместить направление распространения волны с одной из координатных осей, например, с осью 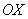. Очевидно, величина перемещения плоскости равной фазы за время наблюдения не зависит от ориентации осей выбранной системы координат. Перемещение плоскости равной фазы волны отсчитывается вдоль перемещения волны, в направлении нормали к плоскости равной фазы, задаваемом единичным вектором 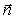. Если учесть, что уравнение плоскости, нормаль которой задаётся вектором 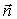(рис.1.10), имеет вид

,

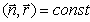где значение константы равно расстоянию от плоскости до начала координат, то величина перемещения волнового фронта, проходящего через начало координат при 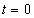, за время наблюдения 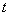будет равно .

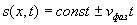С учётом сказанного, выражение для плоской волны, распространяющейся в произвольном направлении, будет иметь вид

.

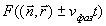В частности для плоской гармонической электромагнитной волны (1.9a):

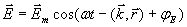,(1.9d)

где 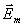- вектор амплитуды колебаний напряжённости электрического поля волны, располагающийся в плоскости перпендикулярной направлению распространения волны.

Рассмотрим зависимость фазовой скорости электромагнитной волны от относительных значений диэлектрической и магнитной проницаемостей 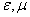от параметров среды распространения. Из формулы (1.13c) следует, что в вакууме при 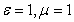фазовая скорость распространения электромагнитной волны равна скорости света 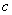в вакууме. Это свойство электромагнитных волн является основанием одним из доказательств электромагнитной природы света. В любой среде, где 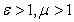скорость распространения электромагнитной волны в 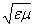раз меньше, чем скорость света в вакууме.Величина

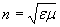,(1.14)

определяющая изменение скорости света в среде по сравнению c вакуумом, называется абсолютным показателем преломления⁴ среды или оптической плотностью среды.

Выражение (1.14) известно, как соотношение Максвелла, впервые установившего зависимость скорости электромагнитных волн от параметров среды их распространения.

Из-за уменьшения в 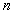раз фазовой скорости электромагнитной волны в среде по сравнению со скоростью света в вакууме уменьшается её длина волны в среде в 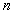раз по сравнению со своим значением в вакууме. Действительно, за период колебаний волны 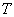волна проходит с меньшей скоростью меньший путь:

,

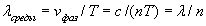где 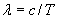- длина волны в вакууме.

По этой причине электромагнитная волна, прошедшая некоторое расстояние 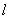в среде с оптической плотностью 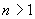получит приращение своей фазы в 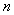раз большее, чем при распространении в вакууме на тоже расстояние. В заключении рассмотрим понятие групповой скорости электромагнитной волны. Необходимость рассмотрения наряду с фазовой скоростью также групповой скорости связана с негармоническими электромагнитными волнами. Оказывается, что электромагнитная волна с произвольной зависимостью от времени и координат точки наблюдения может быть представлена в виде суперпозиции плоских гармонических волн всевозможных частот.

Рис. 1.11.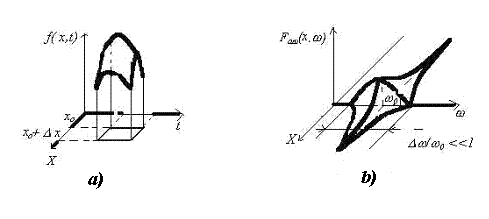

В ряде случаев такая волна представляет собой некоторое ' возмущение ' электромагнитного поля, например, в виде импульса, равного нулю за пределами некоторого интервала 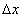(объема 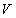) и промежутка времени 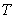(рис.1.11a). Такое волновое поле называют волновым пакетом, если амплитуды гармонических волн, составляющих рассматриваемое возмущение, ' заметно ' отличаются от нуля лишь внутри некоторого интервала 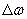' вблизи' средней частоты 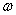0 (рис.1.11b). Если 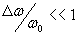, то волна называется почти гармонической или квазигармонической. Волновые пакеты представляют большой практический интерес при рассмотрении взаимодействия электромагнитных волн с веществом, широко используются для передачи информации и пр. Поэтому имеет физический смысл оценка скорости движения волнового пакета или группы волн. Такая скорость называется групповой и обозначается символом 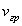. Оказывается, перенос энергии электромагнитной волной осуществляется со скоростью, равной групповой. Расчет групповой скорости 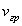электромагнитной волны приводят к следующей формуле (см. задачу 1.3):

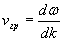.(1.17a)

Это выражение отличается от формулы для расчета фазовой скорости 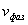плоской гармонической волны частоты :

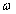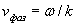.(1.17b)

Это различие имеет очевидную физическую причину, поскольку каждая из составляющих волновой пакет гармонических волн вследствие различия их частот (2.13d) имеет свою фазовую скорость. Можно показать, что фазовая и групповая скорости связаны между собой соотношением:

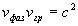,(1.17c)

где 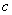- скорость света в среде распространения электромагнитной волны.

Для плоских гармонических электромагнитных волн значения фазовой и групповой скоростей, рассчитываемых по формулам (1.17a) и (1.17b), совпадают.

Date: 2015-05-09; view: 1173; Нарушение авторских прав