
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

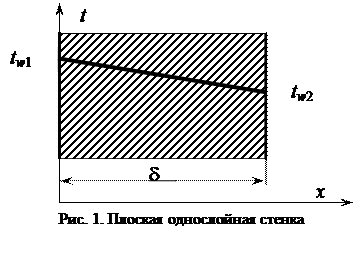
Плоская стенка
|
|
Для плоской однослойной однородной и изотропной стенки с постоянным коэффициентом теплопроводности Х при постоянных температурах tw 1 и tw 2 (рис. 1) на наружных поверхностях стенки температура будет изменяться только в направлении, перпендикулярном плоскости стенки и дифференциальное уравнение теплопроводности запишется в виде:
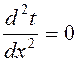 ,
,
граничные условия:
при х =0 t=tw 1,
при x =d t = tw 2,
где d - толщина стенки, м;
х - текущая координата в плоскости, перпендикулярной поверхности стенки, м;
t - текущая температура, °С;
tw 1 и tw 2 - температуры на наружных поверхностях стенки, °С.
После двойного интегрирования получается уравнение распределения температуры в плоской однослойной стенке:
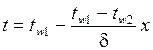 , (1)
, (1)
Для определения количества теплоты, проходящей через единицу поверхности стенки в единицу времени, используют закон Фурье:
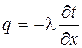 ,
,
учитывая, что
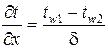 ,
,
получим
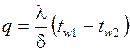 , (2)
, (2)
где q - плотность теплового потока, Вт/м;
l - коэффициент теплопроводности стенки, Вт/(м×К).
Отношение 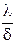 - называется тепловой проводимостью стенки, а обратная величина
- называется тепловой проводимостью стенки, а обратная величина 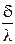 - термическим сопротивлением стенки.
- термическим сопротивлением стенки.
Плотность теплового потока через плоскую многослойную стенку, состоящую из п слоев, рассчитывается по формуле:
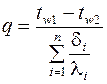 , (3)
, (3)
где d i - толщина i -того слоя стенки, м;
l i - коэффициент теплопроводности i -того слоя стенки, Вт/(м×К).
Величина 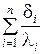 - есть сумма термических сопротивлений всех слоев плоской стенки.
- есть сумма термических сопротивлений всех слоев плоской стенки.
Температура на границах между слоями рассчитывается по формуле
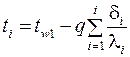 , (4)
, (4)
где ti - температура на границе между i -тым и i +1-вым слоями, °С.
Внутри каждого из слоев с постоянным коэффициентом теплопроводности температура изменяется по прямой линии, а для многослойной стенки в целом изменение температуры представляет собой ломаную линию.
2.2. ЦИЛИНДРИЧЕСКАЯ СТЕНКА
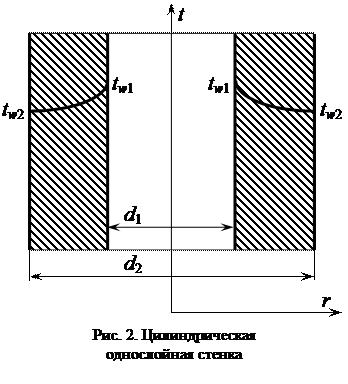
Дифференциальное уравнение теплопроводности однослойной цилиндрической стенки (рис. 2) с постоянными температурами на наружных поверхностях tw 1 и tw 2 и постоянным коэффициентом теплопроводности стенки l запишется в цилиндрических координатах в виде:
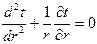 ,
,
граничные условия
при r = d 1/2 t = tw 1,
при r = d 2/2 t = tw 2,
где r - текущая координата, м;
d 1 - внутренний диаметр цилиндрической стенки, м;
d 2. - наружный диаметр цилиндрической стенки, м.
Интегрирование этого уравнения дает распределение температур в однослойной цилиндрической стенке:
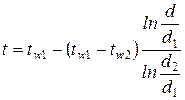 , (5)
, (5)
где d - текущий диаметр цилиндрической стенки, м.
Тепловой поток, проходящий через единицу длины цилиндрической стенки, определяется на основании закона Фурье:
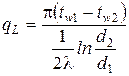 , (6)
, (6)
где qL - линейная плотность теплового потока, Вт/м.
Тепловой поток, проходящий через единицу длины многослойной цилиндрической стенки, состоящей из п слоев, рассчитывают по зависимости:
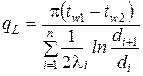 , (7)
, (7)
где di, di +1 - внутренний и наружный диаметры i -того слоя стенки, м.
Выражение для расчета температуры на границах между слоями имеет вид
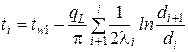 . (8)
. (8)
Date: 2015-05-09; view: 634; Нарушение авторских прав