
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Лекция 4. Основы массопередачи
|
|
4.1. Общие сведения о массообменных процессах
Технологические процессы, скорость протекания которых определяется скоростью переноса вещества из одной фазы в другую, называются массообменными, а аппараты, в которых происходят эти процессы – массообменными аппаратами.
В массообменном аппарате могут производиться разнообразные процессы. Основными и важнейшими из них являются абсорбция, ректификация, экстракция, кристаллизация, адсорбция, сушка, ионнообменные процессы и мембранное разделение.
Абсорбцией называется процесс разделения, основанный на избирательном поглощении газов или паров жидкими поглотителями – адсорбентами. Этот процесс применяется во многих производствах, в которых из смеси газов необходимо извлечь какое-либо вещество или комплекс веществ. В процессе абсорбции имеет место переход вещества или группы веществ из газовой (паровой) фазы в жидкую. Обратный процесс называется десорбцией.
Ректификацией называется процесс разделения смеси жидкостей, имеющих различные температуры кипения при соответствующем давлении, на чистые или обогащенные составляющие в результате противоточного движения потоков пара и жидкости. Процесс имеет большое значение в тех производствах, в которых необходимо частичное или полное разделение жидких однородных смесей на чистые компоненты или их группы. В процессе ректификации имеет место переход вещества или группы веществ из жидкой фазы в паровую, и наоборот.
Экстракцией называется процесс разделения, основанный на извлечении растворенного в одной жидкости вещества или группы веществ, другой жидкостью, которая не смешивается или только частично смешивается с первой. Процесс применяется в тех случаях, когда из раствора необходимо извлечь растворенное вещество или группу веществ. В этом процессе имеет место переход вещества из одной жидкой фазы в другую жидкую фазу.
Адсорбцией называется процесс разделения, основанный на избирательном поглощении газов, паров или растворенных в жидкостях веществ, твердым пористым поглотителем – адсорбентом, способным поглощать одно или несколько веществ из их смеси. Процесс используется в тех производствах, где из смеси газов, паров или растворенных веществ необходимо извлечение того или иного вещества. В этом процессе вещества переходят из газовой или жидкой фаз в твердую. Ионнообменный процесс представляет собой процесс извлечения вещества из раствора, основанный на способности некоторых твердых веществ (ионитов) обменивать свои подвижные ионы на ионы извлекаемого вещества. Процесс применяется для извлечения веществ, находящихся в растворах, в малых концентрациях. В этом процессе вещества переходят из жидкой фазы в твердую.
Сушкой называется процесс удаления влаги из твердых влажных материалов путем ее испарения. Процесс необходим для тех производств, в которых влажные природные вещества предварительно до их переработки или готовые вещества в последней стадии производства должны быть обезвожены. В этом процессе имеет место переход влаги из твердого влажного материала в паровую или газовую фазу.
Кристаллизацией называется процесс разделения, основанный на выделении вещества из жидкой фазы в виде твердой фазы (кристаллов). Процесс имеет место в тех случаях, где требуется получение веществ повышенной чистоты. В этом процессе происходит переход вещества из жидкой фазы в твердую фазу. Обратный процесс – растворение.
Мембранное разделение основано на способности определенных тонких пленок (полупроницаемых мембран) пропускать одни вещества и задерживать другие. В этом процессе вещества переходят через полупроницаемую мембрану из исходной жидкости или газа в выделяемую жидкую или газовую фазу.
Из краткой характеристики следует, что для всех массообменных процессов характерным является переход вещества из одной фазы в другую, или массопередача.
Процессы массопередачи делятся на две группы. К одной группе процессов относятся (например, перегонка, кристаллизация), в которых минимально два вещества, составляющие две фазы, обмениваются компонентами, и непосредственно сами участвуют в массопередаче. В другой группе процессов в большинстве случаев в массопередаче участвуют три вещества: распределяющее вещество (или вещества), составляющие первую фазу; распределяющее вещество (или вещества), составляющие вторую фазу; распределяемое вещество (или вещества), которое переходит из одной фазы в другую. К этой группе относятся процессы: абсорбции, экстракции, адсорбции, сушки.
Одну фазу обозначим буквой G, другую L, а распределяемый компонент М. Поскольку все массообменные процессы обратимы, то распределяемое вещество может переходить в зависимости от концентрации этого вещества в распределяющих фазах из фазы G в фазу L и, наоборот.
Представим для первой группы процессов массопередачи, что распределяемое вещество находится вначале только в фазе G и имеет концентрацию  . В фазе L в начальный момент распределяемого вещества нет и, следовательно, концентрация его в этой фазе
. В фазе L в начальный момент распределяемого вещества нет и, следовательно, концентрация его в этой фазе  =0.
=0.
Если распределяющие фазы привести в соприкосновение, начнется переход распределяемого вещества из фазы G в фазу L, и, в жидкой фазе появится распределяемый компонент с концентрацией отличной от нуля. С момента появления вещества М в фазе L начинается обратный переход его в фазу G. До некоторого момента времени число частиц М, переходящих в единицу времени через единицу поверхности фазового контакта из фазы G в фазу L, больше, чем число частиц, переходящих обратно из фазы L в фазу G.
Через определенный промежуток времени скорости перехода распределяемого вещества из фазы G в фазу L и обратно становятся одинаковыми. Такое состояние называется равновесным. В состоянии равновесия существует строго определенная зависимость между концентрациями распределяемого вещества в фазах, которые при равновесии системы называются равновесными.
Любой концентрации  соответствует равновесная концентрация
соответствует равновесная концентрация 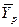 (
( ), и наоборот, любой концентрации
), и наоборот, любой концентрации  соответствует равновесная концентрация
соответствует равновесная концентрация 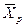 (
( ), т.е. имеют место зависимости вида:
), т.е. имеют место зависимости вида:
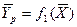 или
или  .
.
Условия равновесия и равновесные зависимости могут быть выражены не только через концентрации, но и через другие параметры, например, энтальпии, химический потенциал.
Знание равновесных концентраций позволяет установить направление течения процесса, которое определяется стремлением к равновесию. Если  >
> 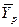 и, следовательно,
и, следовательно, 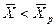 , распределяемое вещество М будет переходить из фазы G в фазу L. При условии
, распределяемое вещество М будет переходить из фазы G в фазу L. При условии  <
< 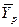 (
( ) распределяемое вещество будет переходить из фазы L в фазу G.
) распределяемое вещество будет переходить из фазы L в фазу G.
Основными задачами, изучаемыми в массопередаче, являются: законы фазового равновесия, позволяющие определить равновесные концентрации и направление течения процесса; движущая сила массообменных процессов; коэффициенты скорости массообменных процессов.
Последние две задачи составляют, так называемую кинетику процесса массопередачи; вопросы фазового равновесия (первая задача) – статику процесса. Эти задачи рассматриваются раздельно при изучении каждого конкретного процесса.
Способы выражения концентраций. Движущая сила массообменных процессов выражается в большинстве случаев концентрациями распределяемого вещества в распределяющих фазах. В расчетной практике пользуются различными способами выражения концентраций, а именно: 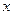 - в кмоль распределяемого компонента/кмоль смеси - мольная доля;
- в кмоль распределяемого компонента/кмоль смеси - мольная доля; 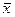 - в кг распределяемого компонента /кг смеси - массовая доля;
- в кг распределяемого компонента /кг смеси - массовая доля; 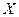 в кмоль распределяемого компонента/кмоль инертного вещества фазы - относительная мольная доля;
в кмоль распределяемого компонента/кмоль инертного вещества фазы - относительная мольная доля;  в кг распределяемого компонента/кг инертного вещества фазы - относительная массовая доля;
в кг распределяемого компонента/кг инертного вещества фазы - относительная массовая доля;  в кмоль распределяемого компонента /м3 фазы - мольная объемная концентрация;
в кмоль распределяемого компонента /м3 фазы - мольная объемная концентрация; 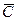 в кг распределяемого компонента/м3 фазы - массовая объемная концентрация.
в кг распределяемого компонента/м3 фазы - массовая объемная концентрация.
Вполне очевидно, что в зависимости от способа выражения концентраций численное значение движущей силы меняется. Между концентрациями существует связь, которая может быть получена в виде простых математических соотношений из физического смысла концентраций.
Например, если рассматривать смесь состоящую из двух компонентов А и В, то связь массовых долей с мольными, и наоборот, определяется по следующим зависимостям:
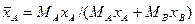 ;
; 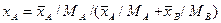 .
.
Соответственно связь относительных массовых и массовых долей
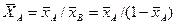 ,
,
объемных концентраций и массовых долей
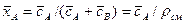 .
.
4.1.1. Основное уравнение массопередачи
Основной закон массопередачи, исходя из общих кинетических закономерностей, формулируется следующим образом: скорость (интенсивность) процесса прямо пропорциональна движущей силе и обратно пропорциональна сопротивлению процесса

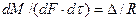 , (4.1)
, (4.1)
где  - количество вещества, перешедшего из одной фазы в другую;
- количество вещества, перешедшего из одной фазы в другую;
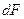 - элементарная поверхность фазового контакта;
- элементарная поверхность фазового контакта; 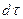 - промежуток времени;
- промежуток времени;  - движущая сила процесса (
- движущая сила процесса (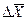 или
или 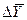 , или разность, выраженная через другие концентрации);
, или разность, выраженная через другие концентрации); 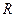 - сопротивление процессу.
- сопротивление процессу.
Если вместо 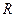 принять обратную величину
принять обратную величину 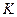 – коэффициент скорости процесса (коэффициент массопередачи) и записать уравнение относительно количества вещества, перешедшего из одной фазы в другую
– коэффициент скорости процесса (коэффициент массопередачи) и записать уравнение относительно количества вещества, перешедшего из одной фазы в другую
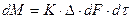 . (4.2)
. (4.2)
Уравнения (4.1) и (4.2) называют основными уравнениями массопередачи.
В аппаратуре, используемой для проведения массообменных процессов, равновесные концентрации не достигаются. Рабочие концентрации распределяемого компонента всегда отличаются от равновесных.
Разность между рабочими равновесными и рабочими концентрациями или, наоборот, характеризующими степень отклонения от равновесия, представляют собой движущую силу массообменных процессов.
4.1.2. Материальный баланс массообменных процессов
Материальный баланс массообменных процессов может быть составлен на основании следующих рассуждений. Рассмотрим взаимодействие двух движущихся фаз с массовыми расходами G - газообразной и L – жидкой, с концентрациями распределяемого компонента  и
и  кг/кг инертных компонентов распределяющих фаз.
кг/кг инертных компонентов распределяющих фаз.
При  >
> 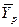 и отсутствии потерь в процессе взаимодействия фаз при параллельных потоках вдоль поверхности раздела концентрация распределяемого компонента в газовой фазе
и отсутствии потерь в процессе взаимодействия фаз при параллельных потоках вдоль поверхности раздела концентрация распределяемого компонента в газовой фазе  уменьшается, а в жидкой
уменьшается, а в жидкой  - увеличивается (рис.4.1).
- увеличивается (рис.4.1).
Для элемента поверхности 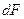
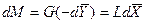 . (4.3)
. (4.3)
Интегрируя уравнение (4.3) в пределах от начальных до конечных концентраций 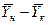 и
и 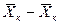 , получим
, получим
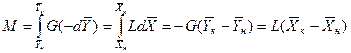
Или
 (4.4)
(4.4)
Интегрируя уравнение (4.3) в пределах от начальных до текущих значений концентраций  и
и 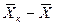 , получим
, получим
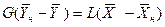 .
.
откуда
 (4.5)
(4.5)
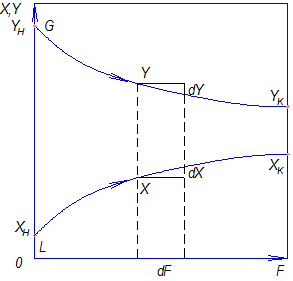
Рис.4.1. Изменение концентраций распределяемого компонента
при прямоточном движении фаз.
Аналогично для противоточного взаимодействия фаз можно получить уравнение
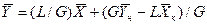 , (4.6)
, (4.6)
 ,
,
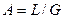 ,
, 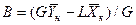 .
.
Так как расходы инертных компонентов носителей газообразной и жидкой фаз постоянны (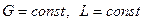 ), из уравнений (4.5) и (4.6) следует, что рабочие концентрации распределяемого вещества в фазах G и L связаны линейной зависимостью. Поэтому процессы массообмена удобно представлять графически в координатах
), из уравнений (4.5) и (4.6) следует, что рабочие концентрации распределяемого вещества в фазах G и L связаны линейной зависимостью. Поэтому процессы массообмена удобно представлять графически в координатах 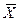
 (рис. 4.2). Уравнение прямой, выражающее зависимость между рабочими концентрациями, называется рабочей линией процесса.
(рис. 4.2). Уравнение прямой, выражающее зависимость между рабочими концентрациями, называется рабочей линией процесса.
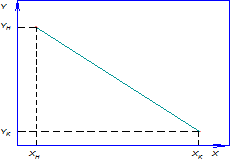
Рис. 4.2. Уравнение рабочей линии процесса.
4.1.3. Движущая сила массообменных процессов
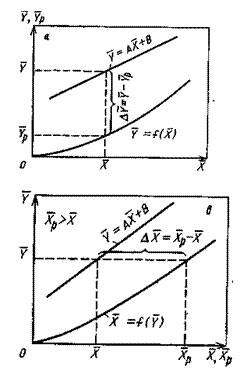
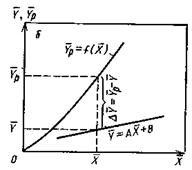
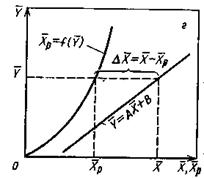
Движущей силой массообменных процессов является разность между рабочей и равновесной концентрациями или, наоборот. Это зависит от того, которая из указанных концентраций больше.
На рис.4.3 приведены возможные варианты выражения движущей силы массообменного процесса при одном и том же направлении перехода распределяемого вещества.
 |  | |||
 | ||||
а) б)
Рис.1.4. Движущая сила массообменного процесса для участка аппарата:
а) по газовой фазе; б) по жидкой фазе.
При этом движущую силу можно выражать либо через концентрации распределяемого вещества в фазе G, либо L. В этой связи уравнения массопередачи, записанные по фазам, имеют вид:
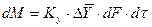 , (4.6)
, (4.6)
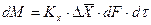 . (4.7)
. (4.7)
Индексы у коэффициента скорости процесса 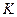 показывают, какие концентрации приняты для выражения движущей силы. В общем случае
показывают, какие концентрации приняты для выражения движущей силы. В общем случае  и
и 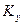
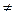
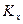 , но всегда выполняется равенство:
, но всегда выполняется равенство:
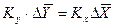 . (4.8)
. (4.8)
Из рис. 4.3. следует, что движущая сила меняется с изменением рабочих концентраций. В этой связи для всего процесса массообмена, протекающего в пределах изменения концентраций от начальных до конечных, должна быть определена средняя движущая сила по газовой фазе  или жидкой -
или жидкой - 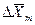 .
.
С учетом средней движущей силы процесса основное уравнение массопередачи для всей поверхности контакта фаз может быть записано в виде:
 , (4.9)
, (4.9)
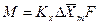 . (4.10)
. (4.10)
При определении движущей силы возможны два случая:
- зависимость между равновесными концентрациями не линейна и определяется функциональной зависимостью самого общего вида типа 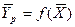 ;
;
- зависимость между равновесными концентрациями линейная - 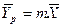 (
( - представляет собой постоянную величину).
- представляет собой постоянную величину).
Определим среднюю движущую силу по фазе G для случая перехода распределяемого компонента из газовой в жидкую фазу. Для элемента поверхности имеем:
 ;
; 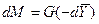
Из сопоставления равенств


для элементарной поверхности фазового контакта имеем
 .
.
После интегрирования в пределах 0 – F и 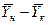 получим:
получим:
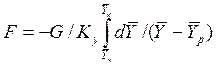 . (4.11)
. (4.11)
Изменим границы интегрирования с целью исключения отрицательного знака перед интегралом, и вставим равенство для 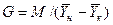 :
:
 . (4.12)
. (4.12)
При выражении движущей силы для жидкой фазы получим аналогичное выражение
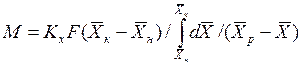 (4.13)
(4.13)
При сравнении уравнений (4.9) и (4.10) с уравнениями (4.12) и (4.13) составим выражения для средних движущих сил по газовой и жидкой фазам:
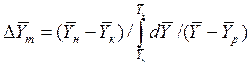 (4.14)
(4.14)
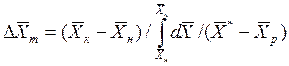 (4.15)
(4.15)
Для случаев, когда между равновесными концентрациями существует прямолинейная зависимость, при определении средней движущей силы используются более простые зависимости, вывод которых приведен в учебной литературе:
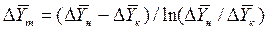 ;
;
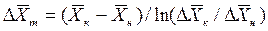 .
.
Интегралы, стоящие в правой части равенств (4.14) и (4.15), называют числами единиц переноса – сокращенно ЧЕП.
ЧЕП для газовой фазы:
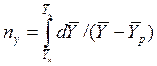 .
.
ЧЕП для жидкой фазы:
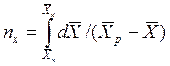 .
.
Число единиц переноса, как следует из уравнений (4.14) и (4.15), определяют по средней движущей силе:
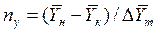 ;
;
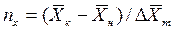 .
.
Физический смысл ЧЕП состоит в том, что эта величина характеризует изменение рабочей концентрации фазы, приходящееся на единицу движущей силы.
Эти соотношения справедливы для всех случаев, когда между рабочими и равновесными концентрациями существуют линейные и нелинейные зависимости.
В случае линейных зависимостей между концентрациями уравнения для вычисления ЧЕП имеют более простой вид:
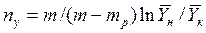 ;
;
 ,
,
где  и
и  - тангенсы угла наклона рабочих и равновесных линий изменения концентраций.
- тангенсы угла наклона рабочих и равновесных линий изменения концентраций.
4.1.4. Модифицированные уравнения массопередачи
В большинстве случаев основное уравнение массопередачи используют в модифицированной форме. Это в первую очередь связано со сложностью геометрического определения поверхности контакта фаз для насадочных, тарельчатых и других массообменных аппаратов.
Если поверхность фазового контакта неопределима, основной характеристикой массообменного аппарата может служить объем, высота или число ступеней фазового контакта.
Если аппарат характеризуется объемом V, тогда 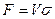 , где
, где 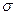 (м2/м3) - удельная поверхность фазового контакта, развиваемая в 1 м3 объема. Модифицированные уравнения масопередачи в этом случае имеют следующий вид:
(м2/м3) - удельная поверхность фазового контакта, развиваемая в 1 м3 объема. Модифицированные уравнения масопередачи в этом случае имеют следующий вид:
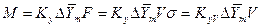 ;
;
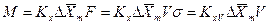 ,
,
где 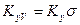 и
и  объемные коэффициенты массопередачи для газовой и жидкой фаз, соответственно.
объемные коэффициенты массопередачи для газовой и жидкой фаз, соответственно.
Достаточно часто за основную характеристику аппарата принимают его высоту. Обозначим площадь поперечного сечения и высоту аппарата, соответственно f и H, тогда  . Из уравнения (4.11) после изменения пределов интегрирования и решения относительно высоты аппарата для газовой фазы получим
. Из уравнения (4.11) после изменения пределов интегрирования и решения относительно высоты аппарата для газовой фазы получим
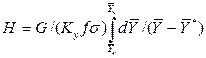 .
.
Комплекс 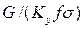 , имеет размерность длины [м] и физический смысл, состоящий в том, что он представляет собой высоту аппарата, эквивалентную единице переноса (ВЕП). Обозначим:
, имеет размерность длины [м] и физический смысл, состоящий в том, что он представляет собой высоту аппарата, эквивалентную единице переноса (ВЕП). Обозначим:
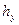
 ,
,
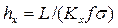 .
.
Тогда уравнения массопередачи по фазам можно записать следующим образом:
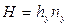 ,
,
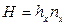 .
.
Высота, эквивалентная единице переноса, по смыслу соответствует величине, обратной объемному коэффициенту массопередачи, а число единиц переноса- величине, обратной движущей силы процесса.
Чем выше интенсивность массопередачи в аппарате, тем меньше в нем величина ВЕП. Значения ВЕП определяются по эмпирическим формулам для различных типов аппаратов. Отмети также, что ВЕП используется только для расчета аппаратов с постоянным поперечным сечением рабочей части.
Для определения ЧЕП в качестве вспомогательного приема может применяться способ определения числа ступеней изменения рабочих концентраций.
Рассмотрим процесс массопередачи, в котором зависимости между равновесными концентрациями и рабочими концентрациями распределяемого вещества представляет прямые линии 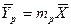 и
и 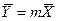 .
.
Если изменение рабочей концентрации распределяемого компонента в газовой фазе от входа в элемент аппарата  до выхода происходит таким образом, что концентрация на выходе
до выхода происходит таким образом, что концентрация на выходе 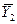 становится равной равновесной концентрации на входе
становится равной равновесной концентрации на входе 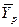 , то такое изменение рабочих концентраций представляет собой ступень изменения концентраций (рис. 4.4).
, то такое изменение рабочих концентраций представляет собой ступень изменения концентраций (рис. 4.4).
 |
Рис.4.4. Ступень изменения концентрации распределяемого компонента.
Число единиц переноса для одной такой ступени (элемента) аппарата составляет:
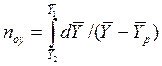 .
.
В рассматриваемом случае
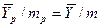 и
и  .
.
Следовательно,
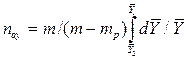 =
= 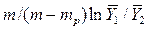 .
.
В то же время 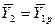 , а
, а 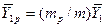 . И тогда
. И тогда
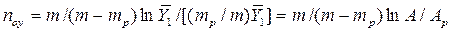 . (4.16)
. (4.16)
Из уравнения (4.16) следует, что только при условии прямых линий 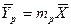 и
и 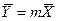 число единиц переноса,
число единиц переноса,  , соответствующее одной ступени изменения концентрации, есть величина постоянная, не зависящая от концентрации.
, соответствующее одной ступени изменения концентрации, есть величина постоянная, не зависящая от концентрации.
Это положение позволяет определить графическим путем общее число единиц переноса для всего аппарата. Допустим, что в процессе массообмена рабочие концентрации изменяются в пределах 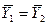 и
и 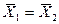 (рис. 4.5).
(рис. 4.5).
Число ступеней изменения рабочих концентраций может быть определено графическим построением ломаной линии между равновесной и рабочей прямыми. В рассматриваемом примере число ступеней изменения концентраций (элементов) равно 4. Эта характеристика может иметь дробное значение. Общее число единиц переноса для аппарата можно определить умножением ЧЕП элемента на число элементов (ступеней контакта), т.е
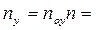
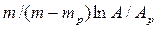
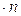 .
.
Число ступеней может быть определено и аналитически. На основе приемов аналитической геометрии (рис. 4.5,а) можно получить:
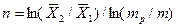 .
.
 |
а) б)
Рис.1.6. Определение числа единиц переноса по числу изменения ступеней концентрации: а) равновесная и рабочая линии процесса прямые;
б) равновесная линия кривая, рабочая – прямая.
Предложенный выше путь определения ЧЕП допускается и в общем случае, когда зависимость 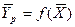 кривая линия (рис. 4.5,б) В этом случае
кривая линия (рис. 4.5,б) В этом случае 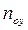 будет переменной величиной.
будет переменной величиной.
Если допустить, что в пределах одной ступени можно с некоторым приближением принять существование линейной равновесной зависимости, для определения общего ЧЕП можно предложить равенство:
 .
.
Использование этого равенства предполагает предварительное графическое определение числа ступеней изменения концентрации и графическое определение величин 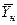 ,
, 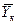 ,
, 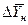 ,
, 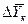 и
и 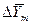 для каждой ступени с последующим определением общего ЧЕП. При принятой в пределах одной ступени линейной зависимости между равновесными концентрациями величина
для каждой ступени с последующим определением общего ЧЕП. При принятой в пределах одной ступени линейной зависимости между равновесными концентрациями величина 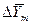 определяется как средняя логарифмическая. В подавляющем большинстве случаев
определяется как средняя логарифмическая. В подавляющем большинстве случаев 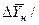
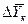 < 2 (при
< 2 (при 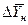 >
> 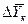 ) величина
) величина 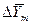 может быть вычислена как средняя арифметическая.
может быть вычислена как средняя арифметическая.
4.1.5. Основные законы массопередачи
В процессах переноса распределяемого компонента из одной фазы в другую различают два случая: 1) перенос из потока жидкости (газа) в поток жидкости, или наоборот; 2)перенос из твердого тела в поток жидкости (газа) или в обратном направлении, т.е. массообмен между пористой твердой фазой и потоком жидкой (газообразной) фазы.
Элементарными законами, которым подчиняется перенос распределяемого вещества из одной фазы в другую, является законы молекулярной диффузии, массоотдачи и массопроводности.
Закон молекулярной диффузии (первый закон Фика). Молекулярная диффузия в газах и растворах жидкостей происходит в результате хаотического движения молекул, не связанного с движением потоков жидкости. В этом случае происходит перенос молекул распределяемого компонента из областей высоких концентраций в область низких концентраций. Кинетика переноса подчиняется в этом случае первому закону Фика, формулировка которого аналогична закону теплопроводности: количество вещества, продиффундировавшего в пределах фазы, пропорционально градиенту концентраций, площади, перпендикулярной направлению диффузионного потока, и времени:
 , (4.16)
, (4.16)
где  - коэффициент пропорциональности, или коэффициент диффузии.
- коэффициент пропорциональности, или коэффициент диффузии.
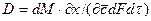
Коэффициент диффузии показывает, какое количество вещества диффундирует через поверхность 1 м2 в течение 1 с при разности концентраций на расстоянии 1 м, равной единице.
Знак минус в правой части уравнения показывает, что при молекулярной диффузии направление перемещения вещества и градиент концентраций противоположны друг другу.
Размерность коэффициента зависит от способа выражения концентрации распределяемого компонента. Если это объемные концентрации, то размерность коэффициента следующая:
 =[(кг·м·м3)/(м2·с·кг)]=[м2/с].
=[(кг·м·м3)/(м2·с·кг)]=[м2/с].
Коэффициент диффузии не является постоянной величиной. Это достаточно малая величина для газов. Она на четыре порядка выше, чем для жидкостей. Коэффициент диффузии увеличивается с ростом температуры и уменьшается с повышением давления. Если в газах коэффициент диффузии не зависит от концентрации диффундирующего вещества, то в жидкостях это влияние особенно значимо для неразбавленных растворов.
 |
Дифференциальное уравнение молекулярной диффузии
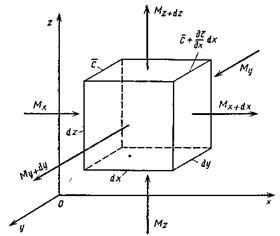
(второй закон Фика). Для вывода дифференциального уравнения, как это было принято для всех рассмотренных случаев в гидростатике и теплопроводности, выделяется в неподвижной среде элементарный параллелепипед с ребрами dx, dy, dz (рис.4.6).
Рис.4.6. К выводу дифференциального уравнения молекулярной диффузии.
Если через этот элементарный параллелепипед за счет молекулярной диффузии перемещается распределяемое вещество, то через левую, заднюю и нижнюю грани за промежуток времени 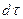 в него входят количества вещества соответственно
в него входят количества вещества соответственно  и
и 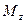 , а через противоположные грани – правую, переднюю, и верхнюю – входят количества вещества соответственно
, а через противоположные грани – правую, переднюю, и верхнюю – входят количества вещества соответственно  и
и 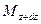 . Следовательно элемент за промежуток времени
. Следовательно элемент за промежуток времени 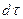 приобретает диффундирующее вещество в количестве:
приобретает диффундирующее вещество в количестве:
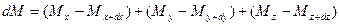 .
.
При этом концентрация диффундирующего вещества повышается на 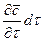 .
.
Согласно основному молекулярной диффузии,  ,
,

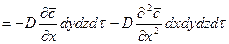 .
.
Следовательно,
 ;
;
Аналогично найдем:
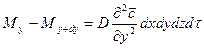 ;
;
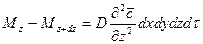 .
.
Суммируя левые и правые части трех последних равенств, получим:
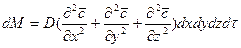 .
.
С другой стороны, тот же прирост количества диффундирующего вещества в элементе можно найти умножением объема элемента на изменение концентрации за время 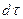 , т.е.
, т.е.
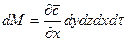
Приравнивая правые части двух последних зависимостей, получим уравнение молекулярной диффузии:

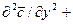
 . (4.17)
. (4.17)
Левая часть этого уравнения характеризует локальное изменение концентрации распределяемого компонента в неподвижном элементе, выделенном в распределяющей фазе.
Закон массотдачи (Щукарева). Основной закон массоотдачи, или конвективной диффузии, впервые был сформулирован Щукаревым при изучении кинетики растворения твердых тел. Этот закон является аналогом закона теплоотдачи, сформулированным Ньютоном.
Количество вещества, перенесенного от поверхности раздела фаз в воспринимающую фазу, пропорционально разности концентраций у поверхности раздела фаз и в ядре потока воспринимающей фазы, поверхности фазового контакта и времени
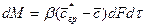 , (4.18)
, (4.18)
где 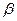 - коэффициент массоотдачи, характеризующий перенос вещества в пределах фазы конвекцией и диффузией одновременно;
- коэффициент массоотдачи, характеризующий перенос вещества в пределах фазы конвекцией и диффузией одновременно;  - концентрация распределяемого компонента у поверхности раздела распределяющей фазы;
- концентрация распределяемого компонента у поверхности раздела распределяющей фазы;  - концентрация распределяемого компонента в ядре потока распределяющей фазы.
- концентрация распределяемого компонента в ядре потока распределяющей фазы.
Отметим, что концентрация на границе  рассматривается как равновесная концентрация.
рассматривается как равновесная концентрация.
Размерность коэффициента массоотдачи можно установить из уравнения:
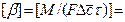 [(кг·м3)/(м2·с·кг)]=[м/с].
[(кг·м3)/(м2·с·кг)]=[м/с].
Коэффициент массотдачи показывает, какое количество вещества передается от поверхности раздела фаз в воспринимающую фазу через поверхность в 1 м2 в течение 1 с при разности концентраций равной единице.
Для установившегося процесса коэффициент массоотдачи и концентрации сохраняют постоянное значение в рассматриваемом объеме:
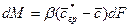 . (4.19)
. (4.19)
Если коэффициент массоотдачи сохраняет постоянное значение для всей поверхности, то уравнение принимает вид:
 . (4.20)
. (4.20)
Дифференциальное уравнение массоотдачи (конвективной диффузии). В основу рассмотрения явления конвективной диффузии положена теория диффузионного пограничного слоя.
Согласно этой теории распределяемое вещество переносится из ядра потока жидкости к границе раздела фаз непосредственно потоками жидкости и молекулярной диффузией (рис.4.7). Рассматриваемая система состоит из двух частей: ядра и пограничного диффузионного слоя, включающего в себя достаточно тонкий ламинарный подслой. В ядре перенос вещества осуществляется преимущественно токами жидкости в условиях достаточной турбулентности. Концентрация распределяемого компонента в ядре турбулизированного потока фазы принимается постоянной.
По мере приближения к пограничному диффузионному слою турбулентный перенос затухает и с приближением к границе раздела фаз в ламинарном подслое начинает превалировать перенос за счет молекулярной диффузии. Соответственно этому появляется градиент концентрации распределяемого компонента, увеличивающийся по мере приближения к границе. Таким образом, область диффузионного пограничного слоя – это область проявления и роста молекулярной диффузии от малого до максимального значения.
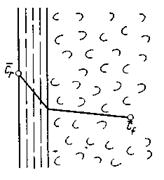 |
Рис.4.7. К формулировке закона конвективной диффузии.
При наличии конвективной диффузии концентрация распределяемого компонента изменяется не только вследствие молекулярной диффузии, но и механического переноса его из одной области пространства в другую. В этом случае концентрация распределяемого компонента будет функцией не только координат x, y, z и времени 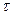 , но и составляющих скорости перемещения частиц потока
, но и составляющих скорости перемещения частиц потока 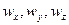 .
.
При конвективной диффузии бесконечно малый элемент потока перемещается из одной точки пространства в другую. В этом случае изменение концентрации распределяемого компонента может быть выражено субстанциональной производной, которая учитывает изменение ее во времени и изменения, связанные с перемещением элемента из одной точки пространства в другую:
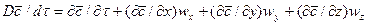 . (4.21)
. (4.21)
В этом равенстве 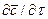 представляет собой локальное изменение концентрации распределяемого компонента, а комплекс
представляет собой локальное изменение концентрации распределяемого компонента, а комплекс  - конвективное изменение концентрации.
- конвективное изменение концентрации.
Если в уравнении молекулярной диффузии (4.17) заменить локальное изменение концентрации 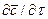 полным
полным 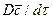 , в соответствие с уравнением (4.21), то можно получить дифференциальное уравнение конвективной диффузии:
, в соответствие с уравнением (4.21), то можно получить дифференциальное уравнение конвективной диффузии:
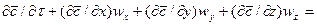

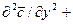
 (4.22)
(4.22)
Уравнение конвективной диффузии необходимо решать совместно с уравнениями движения Навье-Стокса, поскольку переменными являются концентрации и проекции скорости потока. Однако эта система уравнений не имеет аналитического решения и для получения расчетных зависимостей по массообмену приходится прибегать к теории подобия.
4.1.6. Подобие процессов переноса массы
Системы уравнений конвективной диффузии и уравнений движения не имеют общего решения. Поэтому также, как и в случае гидромеханических и теплообменных процессов, можно методами теории подобия найти связь между переменными, характеризующими процесс переноса в потоке фазы, в виде обобщенного (критериального) уравнения массоотдачи.
В это уравнение входят критерии подобия, которыми описываются подобие процессов массоотдачи на границе фазы (подобие граничных условий) и в основной массе (ядре) фазы.
Подобие граничных условий можно установить, допуская наличие пограничного слоя, в котором перенос осуществляется только молекулярной диффузией. Количество вещества, переходящего из ядра к границе фазы, составляет
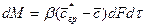 .
.
То же количество вещества переносится молекулярной диффузией через пограничный слой
 .
.
Приравнивая выражения и проведя сокращения, получим зависимость, характеризующую подобие условий переноса на границе фазы:
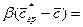
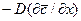 .
.
Обозначив 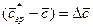 , запишем это уравнение в виде:
, запишем это уравнение в виде:
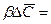
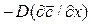 .
.
Из этого уравнения делением левой на правую часть, сократив подобные члены и опустив знак минус, получим безразмерный комплекс, который для подобных систем является одинаковым (одним и тем же), т.е. 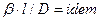 .
.
Данный комплекс величин, при выражении их в единицах одной системы, является безразмерным и в соответствии с первой теоремой подобия представляет собой критерий подобия. Этот комплекс называют диффузионным критерием Нуссельта
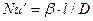 .
.
Диффузионный критерий Нуссельта выражает отношение интенсивности переноса вещества в ядре фазы к интенсивности переноса в диффузионном пограничном подслое, где массообмен определяется молекулярной диффузией.
Из дифференциального уравнения конвективной диффузии
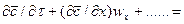
 ……,
……,
получаем безразмерные комплексы делением всех членов уравнения на 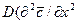 :
:

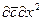 /
/  ;
; 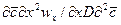 .
.
Вычеркнув в полученных комплексах символы дифференцирования и направления, после сокращения получим диффузионный критерий Фурье:

или, чтобы исключить математические действия с малыми величинами в виде
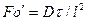 ,
,
и диффузионный критерийПекле
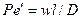 .
.
Равенство критериев 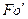 в сходственных точках подобных систем – необходимое условие подобия неустановившихся процессов массоотдачи. Это равенство характеризует постоянство отношения изменения концентрации во времени к изменению концентрации вследствие чисто молекулярного переноса.
в сходственных точках подобных систем – необходимое условие подобия неустановившихся процессов массоотдачи. Это равенство характеризует постоянство отношения изменения концентрации во времени к изменению концентрации вследствие чисто молекулярного переноса.
Критерий  выражает меру отношения массы вещества, перемещаемой путем конвективного переноса и молекулярной диффузии, в сходственных точках подобных систем.
выражает меру отношения массы вещества, перемещаемой путем конвективного переноса и молекулярной диффузии, в сходственных точках подобных систем.
Подобие распределения концентраций и одновременно подобие скоростей в потоках соблюдается в общем случае в геометрически подобных системах при следующих условиях:
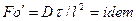 ;
;  ;
; 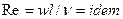 .
.
Во многих случаях вместо критерия  используют отношение критериев
используют отношение критериев  и
и  , которое представляет собой диффузионный критерий Прандтля:
, которое представляет собой диффузионный критерий Прандтля:
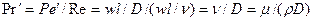 .
.
В критерий  входят только величины, отражающие физические свойства потока. Этот критерий характеризует постоянство отношения физических свойств жидкости (газа) в сходственных точках подобных потоков. Критерий Прандтля рассматривается как мера подобия профилей скорости и концентрации в процессах массоотдачи.
входят только величины, отражающие физические свойства потока. Этот критерий характеризует постоянство отношения физических свойств жидкости (газа) в сходственных точках подобных потоков. Критерий Прандтля рассматривается как мера подобия профилей скорости и концентрации в процессах массоотдачи.
При  1 толщина диффузионного подслоя равна толщине гидродинамического ламинарного подслоя.
1 толщина диффузионного подслоя равна толщине гидродинамического ламинарного подслоя.
Необходимой предпосылкой подобия процессов массоотдачи является соблюдение гидродинамического подобия, которое требует, чтобы в сходственных точках подобных потоков были равны не только критерии Рейнольдса, но и критерии Фруда. Критерий Фруда часто бывает удобно заменить критерием Галилея (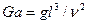 ) или Грасгофа (
) или Грасгофа ( , где
, где 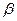 - коэффициент объемного расширения), в которые не входит скорость потока.
- коэффициент объемного расширения), в которые не входит скорость потока.
Определяемой величиной при расчете массоотдачи является коэффициент 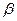 , величину которого находят из диффузионного критерия Нуссельта. Этот критерий является определяемым.
, величину которого находят из диффузионного критерия Нуссельта. Этот критерий является определяемым.
Полученные критерии подобия дают возможность найти уравнение подобия конвективной диффузии:
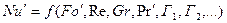 ,
,
где Г1, Г2, … Гn – симплексы геометрическое подобие систем, представляющие отношения характерных геометрических размеров l1, l2, … ln к некоторому определяющему размеру l0.
Применительно к конкретным задачам массообмена общее уравнение подобия может быть упрощено. При рассмотрении стационарных процессов из уравнения исключается критерий Фурье
 .
.
При вынужденном движении можно пренебречь естественной конвекцией
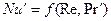 или
или 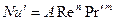 .
.
В условиях естественной конвекции
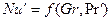 или
или 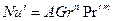 .
.
Расчетные зависимости называются критериальными уравнениями массоотдачи. Численные значения входящих в них постоянных коэффициентов A и показателей степеней n и m устанавливают при обработке опытных данных.
4.1.7. Связь коэффициентов массопередачи и массоотдачи
Чтобы установить аналиттческую зависимость между коэффициентами массопередачи и массоотдачи, принимают, что на границе раздела фаз достигается равновесие. Это предположение равносильно допущению о том, что сопротивлением переносу вещества через границу раздела фаз можно пренебречь. Отсюда как следствие вытекает положение об аддитивности фазовых сопротивлений, которое является одной из предпосылок к расчету коэффициента массопередачи.
Допустим, что распределяемый компонент переходит из фазы G в фазу L и движущая сила выражается в концентрациях фазы G. При установившемся процессе массопередачи количество вещества, переходящее из одной фазы в другую фазу, определяется по уравнению:
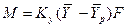 .
.
Для упрощения рассмотрим случай, когда равновесная зависимость между равновесными концентрациями представляют линейную зависимость 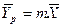 , где m – тангенс угла наклона линии равновесия.
, где m – тангенс угла наклона линии равновесия.
Из уравнения равновесия следует
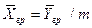 и
и 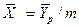 .
.
Уравнение массоотдачи для жидкой фазы
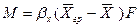 .
.
Подставляя значения 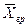 и
и 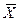 в уравнение массоотдачи, получим
в уравнение массоотдачи, получим
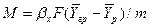
откуда
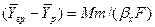 . (4.23)
. (4.23)
Из уравнения массоотдачи для газовой фазы

получим
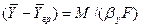 . (4.24)
. (4.24)
Складывая выражения (4.23) и (4.24) и исключая неизвестную концентрацию на границе раздела фаз получим
 .
.
Из уравнения массопередачи следует, что
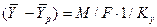 .
.
Приравнивая правые части и, сокращая подобные члены, получим выражение для коэффициента массопередачи по газовой фазе
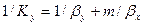 . (4.25)
. (4.25)
При выражении коэффициента массопередачи в концентрациях жидкой фазы получим
 . (4.26)
. (4.26)
Левые части уравнений представляют собой общее сопротивление переносу вещества из фазы в фазу, т.е. сопротивление массопередаче, а правые части – сумму сопротивлений массоотдаче в фазах. Поэтому эти зависимости являются уравнениями аддитивности фазовых сопротивлений. Эти уравнения справедливы и для случая, если линия равновесия является кривой.
4.1.8. Массопередача с твердой фазой
В основе таких распространенных процессов пищевых производств как адсорбция, сушка, экстракция из твердых пористых материалов, лежат общие закономерности массообмена с участием твердой фазы.
Массопередача между твердой и движущейся жидкой (газовой) фазой складывается из двух процесов: 1) перемещением распределяемого компонета внутри пор твердого тела к поверхности раздела фаз (или от нее) вследствие внутренней массоотдачи, или массопроводности; 2) перенос того же вещества от поверхности раздела фаз в поток жидкости (газа, пара) за счет массоотдачи. Иными словами, массопередача является результатом внутренней и внешней диффузии.
В качестве закона, которому подчиняется кинетика переноса распределяемого вещества в твердом теле, принят закон, аналогичный закону теплопроводности: количество вещества, переместившегося в твердой фазе за счет массопроводности, пропорционально градиенту концентрации, площади, перпендикулярной направлению потока вещества, и времени, т.е.
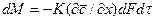 .
.
В этом уравнении коэффициент скорости процесса 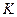 называется коэффициентом массопроводности. Коэффициент массоопроводности аналогичен коэффициенту диффузии, но при одинаковых условиях меньше его, поэтому его иногда называют коэффициентом «стесненной диффузии».
называется коэффициентом массопроводности. Коэффициент массоопроводности аналогичен коэффициенту диффузии, но при одинаковых условиях меньше его, поэтому его иногда называют коэффициентом «стесненной диффузии».
Процесс перемещения вещества внутри твердого тела может быть описан дифференциальным уравнением массопроводности:
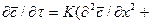
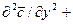
 . (4.27)
. (4.27)
Вполне очевидно, что 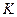 не является постоянной величиной. Он зависит от природы процесса (адсорбция, сушка, выщелачивание), от ряда факторов, определяющих значение коэффициента молекулярной диффузии, и от структуры твердого пористого тела.
не является постоянной величиной. Он зависит от природы процесса (адсорбция, сушка, выщелачивание), от ряда факторов, определяющих значение коэффициента молекулярной диффузии, и от структуры твердого пористого тела.
Дифференциальное уравнение массопроводности должно быть дополнено уравнением, характеризующим условия на границе раздела твердой и жидкой фаз. К элементарной площадке на границе раздела подводится вещество из твердой фазы в количестве
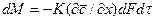 .
.
От элементарной площадки в омывающую фазу отводится
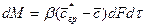 . (4.28)
. (4.28)
Приравнивая правые части этих уравнений, получим дифференциальное уравнение, характеризующие условия на границе раздела фаз:
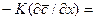
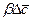 . (4.29)
. (4.29)
Из уравнения (1.29) может быть получен безразмерный комплекс делением правой на левую часть, который называется диффузионным критерием Био
 .
.
Критерий Био выражает отношение интенсивности переноса вещества в ядре омывающей фазы к интенсивности переноса в твердом материале, где массообмен связан с массопроводностью.
Из дифференциального уравнения массопроводности

получаем безразмерный комплекс делением правой на левую часть, который называется диффузионным критерием Фурье
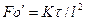 ,
,
характеризующим изменение скорости потока вещества, перемещаемого массопроводностью в твердом теле.
Дифференциальное уравнение массопроводности для одномерного перемещения вещества по толщине пластины (рис.4.8) имеет аналитическое решение в виде:
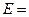


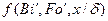 , (4.30)
, (4.30)
где 
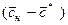 - безразмерная концентрация распределяемого вещества в твердой фазе с координатой
- безразмерная концентрация распределяемого вещества в твердой фазе с координатой 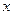 ;
;  - текущая концентрация в точке
- текущая концентрация в точке 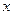 в момент времени
в момент времени 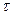 ;
; 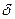 - определяющий размер твердого тела;
- определяющий размер твердого тела; 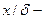 безразмерная координата точки, в которой концентрация равна
безразмерная координата точки, в которой концентрация равна  .
.
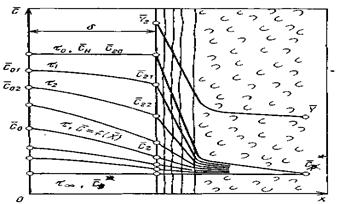 |
В рассматриваемом случае в момент времени
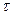 концентрация внутри пластины меняется от
концентрация внутри пластины меняется от 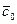 до
до 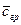 , в зависимости от координаты
, в зависимости от координаты 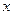 , т.е.
, т.е. 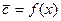 .
.
Рис.4.8. Осесимметричное изменение концентрации распределяемого компонента по толщине пористой твердой пластины во времени.
Date: 2015-05-09; view: 2135; Нарушение авторских прав