Передача тепла теплопроводностью

Закон Фурье. Основным законом передачи тепла теплопроводностью является закон Фурье, согласно которому количество тепла , передаваемого теплопроводностью, пропорционально градиенту температуры 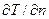, времени 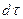и площади сечения 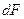, перпендикулярного направлению теплового потока:

.

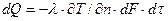Коэффициент пропорциональности в этом уравнении называется коэффициентом теплопроводности. Этот коэффициент характеризует способность тел проводить тепло. Согласно уравнению теплопроводности, коэффициент имеет следующую размерность:

.

Коэффициент теплопроводности показывает, какое количество тепла проходит вследствие теплопроводности через 1 м² поверхности в единицу времени при разности температур 1 К, приходящейся на 1 м длины нормали к изотермической поверхности.

Коэффициент теплопроводности веществ зависит от их природы и агрегатного состояния. Пределы изменения: для газов - 0,005–0,5; для жидкостей - 0,08–0,7; для металлов – 2,3–458; теплоизоляционных и строительных материалов – 0,02–3,0 Вт/(мК).

Для металлов, применяемых при изготовлении аппаратов пищевых производств, коэффициенты теплопроводности составляют: для нержавеющей стали – 14–23; свинца – 35; углеродистой стали – 45; чугуна – 63; алюминия – 204; меди – 384; серебра – 458 Вт/(мК).

Коэффициенты теплопроводности веществ зависят от температуры и давления. Для газов они возрастают с повышением температуры и мало зависят от давления. Для жидкостей с увеличением температуры уменьшаются, за исключением воды и глицерина. Теплопроводность твердых тел в большинстве случаев растет с повышением температуры.

Дифференциальное уравнение теплопроводности. Процесс распространения тепла теплопроводностью может быть описан дифференциальным уравнением, полученным на основе закона сохранения энергии, в предположении неизменности физических свойств тела по направлениям и во времени ().

Для вывода дифференциального уравнения рассматривается элементарный параллелепипед, выделенный из тела, с гранями (рис. 3.1).

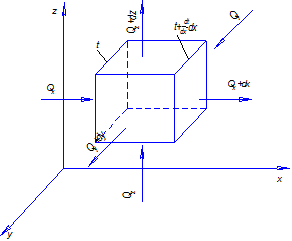
Рис. 3.1. Элементарный параллелепипед к выводу дифференциального уравнения

теплопроводности

Количество тепла, входящего в параллелепипед через грань в направлении оси 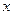за время 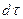, по закону Фурье:

,

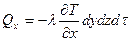выходящего через противоположную грань параллелепипеда:

.

Разность между количеством тепла, вошедшего и вышедшего через грань в направлении оси 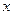за время :

.

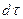Для всех граней параллелепипеда:

.

На основе закона сохранения энергии количество тепла представляет тепло, которое идет на изменение энтальпии параллелепипеда за время :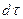

.

Сопоставив выражения для и произведя сокращения, получим дифференциальное уравнение теплопроводности

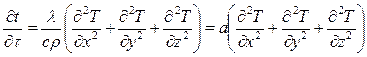
или в сокращенной записи:

.

Множитель, входящий в уравнение теплопроводности , называется коэффициентом температуропроводности. Этот коэффициент характеризует теплоинерционные свойства веществ: при прочих равных условиях быстрее нагревается или охлаждается то тело, которое обладает большим коэффициентом температуропроводности:

.

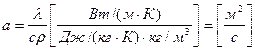Уравнение позволяет решать задачи, связанные с распространением тепла теплопроводностью, как при неустановившихся, так и при установившихся тепловых потоках. При решении конкретных задач дифференциальное уравнение дополняется начальными и граничными условиями.

Теплопроводность плоской стенки. Рассмотрим передачу тепла теплопроводностью через плоскую стенку, длина и ширина которой бесконечно велики по сравнению с ее толщиной 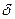в направлении оси .

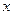Температуры стенок равны 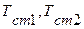, причем . При установившемся процессе количество тепла, подведенного к стенке и отведенного от нее, равны между собой и не изменяются во времени. В связи с тем, что температура меняется только в направлении оси 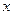, дифференциальное уравнение одномерного температурного поля имеет вид:

.

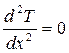Интегрирование этого уравнения приводит к функции

.

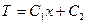Константы интегрирования определяются исходя из следующих граничных условий:

при 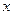= 0, ,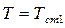

;

при , ,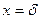

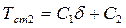
или ,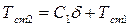

откуда .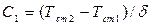

Подставив значения констант 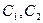в уравнение, получим

.

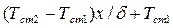Тогда для температурного градиента:

.

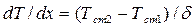После подстановки выражения для температурного градиента в уравнение теплопроводности получим для количества тепла

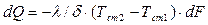
или

.

Если плоская стенка состоит из 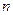слоев, отличающихся друг от друга теплопроводностью и толщиной, то при установившемся процессе через каждый слой стенки пройдет одно и то же количество тепла, которое может быть выражено для различных слоев уравнениями:

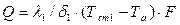или

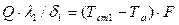
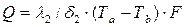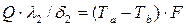
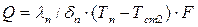или

…………………………………………………..

или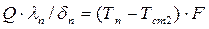

Произведем сложение правых и левых частей этих уравнений. В результате получим

,

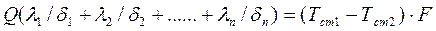откуда

.

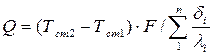Зависимости для расчета теплового потока через однослойную и многослойную цилиндрические стенки приведем без вывода:

;

.

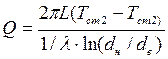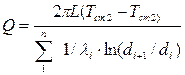При 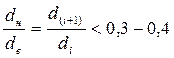расчет теплового потока можно вести как для плоской стенки.

Date: 2015-05-09; view: 568; Нарушение авторских прав