
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Дифференциальное уравнение конвективного теплообмена
|
|
При конвективном теплообмене тепло распространяется в жидкости одновременно теплопроводностью и конвекцией. Процесс распространения тепла теплопроводностью описывается дифференциальным уравнением вида:
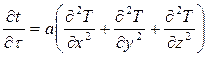 .
.
Левая часть этого уравнения представляет локальное изменение температуры элемента, выделенного в неподвижной среде.
При конвективном теплообмене элемент перемещается из одной точки пространства в другую. В этом случае изменение температуры элемента может быть выражено при помощи субстациональной производной, учитывающей одновременно изменения параметра во времени и в пространстве, связанные с перемещением элемента из одной точки в другую. Субстанциональная производная, характеризующая полное изменение температуры движущего элемента, может быть записана в следующем виде:
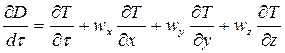 .
.
Если в уравнении теплопроводности заменить локальное изменение температуры полным, то можно получить дифференциальное уравнение конвективного переноса тепла Фурье – Кирхгофа:
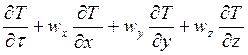
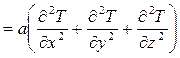 .
.
Для полного математического описания это уравнение должно быть дополнено уравнением, характеризующим условия на границе раздела движущейся среды и твердого тела.
У поверхности твердого тела, находящегося в движущейся среде, всегда имеется пограничный слой толщиной 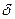 , через который тепло распространяется теплопроводностью (рис. 3.3).
, через который тепло распространяется теплопроводностью (рис. 3.3).
Количество переданного через этот слой тепла при его распространении от теплообменной поверхности к ядру жидкостного потока можно определить по закону Фурье:
 .
.
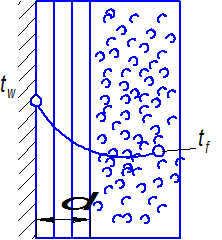
Рис. 3.3. Изменение температуры в движущей среде при конвективном теплообмене
Это же количество тепла можно найти по закону Ньютона:
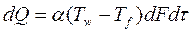 .
.
Приравнивая правые части последних равенств, получаем уравнение, характеризующее условия теплообмена на границе раздела движущейся среды и твердого тела:
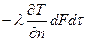
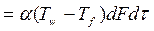 .
.
Полученное уравнение и дифференциальное уравнение конвективного массообмена в полной мере описывают процесс, но для их решения необходимо еще знать проекции скоростей потока жидкости по соответствующим координатам.
С этой целью система уравнений должна включать дифференциальные уравнения движения и неразрывности. Но, как уже было сказано выше, такая система уравнений не имеет аналитического решения. Не имеет аналитического решения также система с дифференциальным уравнениям конвективного теплообмена.
Таким образом, аналитически не может быть установлено ни температурное поле в движущейся среде, ни величина теплового потока. Для решения конкретных инженерных задач приходится прибегать к эксперименту и обобщениям с использованием методов теории подобия.
Date: 2015-05-09; view: 633; Нарушение авторских прав