Фильтрование

Фильтрованием называется процесс разделения неоднородных систем с использованием пористых пе­регородок, которые задерживают твердую фазу и пропускают дисперсионную среду. По характеру дисперсионной среды различают филь­трование жидкостей и фильтрование газов.

Процессы промышленного фильтро­вания могут быть разделены на две группы, отличаю­щиеся своеобразием механизма. К одной группе отно­сятся процессы фильтрования с образованием осадка, к другой группе - с закупориванием пор. Возможен также промежуточный вид фильтрования, когда твердые частицы проникают в поры фильтровальной перегородки и образуют на ней слой осадка.

Обычно размер пор фильтрующей перегородки боль­ше размера взвешенных частиц. В процессе фильтрования с образованием осадка входы в капил­ляры фильтровальной перегородки перекрыва­ются сводами из взвешенных частиц, которые предохраняют каналы от засорения. Образуется осадок, толщина которо­го увеличивается по мере фильтрования. После образования слоя осадок начинает играть основную роль задержания частиц, размеры которых больше размеров капилляров осадка. По мере роста толщины осадка увеличивается сопротив­ление фильтрованию, уменьшается скорость процесса.

В процессе фильтрования с закупориванием пор взвешенные частицы проникают в капилляры и застревают там. Накапливаясь в порах фильтра, частицы осадка закупоривают их. По мере увеличения числа закупорен­ных пор живое сечение фильтра уменьшается и сопро­тивление растет.

Тот или иной вид фильтрования зависит от свойств суспензии, фильтрующей перегородки, давле­ния фильтрования, поэтому одна и та же суспензия мо­жет фильтроваться по-разному.

В производственных условиях под фильтрованием понимают не только операцию разделения суспензии на фильтрат и осадок с помощью фильтровальной перегородки, но и последующие операции промывки, продувки и сушки осадка на фильтре.

Уравнения фильтрования. Скорость процесса фильтрования пропорциональна движущей силе и обратно пропорциональна сопротивлению процесса:

,

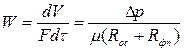где 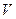- объем фильтрата; 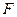- поверхность фильтрования; 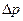- разность давлений; 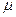- вязкость жидкойфазы суспензии; 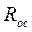- сопротивление осадка; 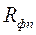- сопротивление фильтровальной перегородки.

Разность давлений 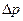может быть создана при повышении дав­ления над фильтровальной перегородкой или созданием вакуума под ней. В этой связи различают фильтры, работающие под давлением, и фильтры, работающие под вакуумом. Схема фильтра, в котором процесс осуществляется под действием перепада давления с отложением осадка, приведена на рис. 2.45.

Теория фильтрования основана на предположении о том, что в капиллярах осадка движение жидкости но­сит ламинарный характер.

По мере увеличения количества фильтрата, пропу­щенного фильтром, высота слоя осадка на его поверхно­сти увеличивается. Это приводит к увеличению сопротив­ления 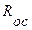. Величину 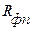можно считать приблизительно постоянной, пренебрегая при этом некоторым возможным ее увеличением вследствие проникновения в поры перегородки твердых частиц. Если величину 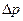поддерживать постоянной, то, как видно из уравнения, скорость фильтрования будет уменьшаться. Такой режим фильтрования называ­ется фильтрованием при постоянном давле­нии.

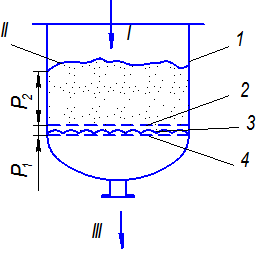
Рис. 2.45. Схема фильтра: 1 – емкость; 2 – фильтрующая ткань; 3 – дренажная сетка;

4 – опорная решетка; I – cуспензия; II – осадок; III – фильтрат

Для интегрирования уравнения необходимо установить зависимость между сопротивлением слоя осадка и объемом полученного фильтрата. Введем следующие обозначения: 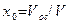; - объем осадка.

Тогда высота слоя осадка равна

,

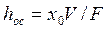а сопротивление слоя осадка можно выразить равенством

,

где 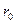- удельное сопротивление слоя осадка.

Из этого равенства следует, что величина 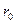характеризует сопротивление, оказываемое потоку жидкой фазы равномерным слоем осадка толщиной 1 м.

Подставив значение в зависимость скорости процесса, получим

.

Если принять, что сопротивлением фильтровальной перегородки можно пренебречь, из предыдущего равенства получим

.

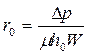При динамическом коэффициенте вязкости 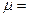1 Па∙с, высоте осадка 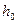= 1 м и скорости фильтрования 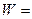1 м/с удельное сопротивление осадка .

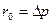Таким образом, удельное сопротивление осадка численно равно разности давлений, необходимой для того, чтобы жидкая фаза с вязкостью равной единице фильтровалась со скоростью 1 м/с через слой осадка толщиной 1 м.

Жидкость с такой большой вязкостью может существовать только гипотетически. В связи с этим на практике такой большой разности давлений быть не может. Для сильно сжимаемых осадков значение 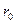достигает 10¹² м ^-2 и более.

Если принять 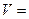0, что соответствует началу процесса фильтрования, когда на фильтровальной перегородке еще не образовался слой осадка, из уравнения для скорости фильтрования получим

.

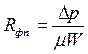При динамическом коэффициенте вязкости 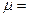1 Па∙с и скорости фильтрования 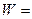1 м/с сопротивление фильтровальной перегородки . Это означает, что сопротивление фильтровальной перегородки численно равно разности давлений, необходимой для того, чтобы жидкая фаза с вязкостью равной единице проходила через фильтровальную перегородку со скоростью 1 м/с. Для ряда фильтровальных перегородок величина имеет порядок 10¹⁰ м ^-1.

При постоянной разности давлений 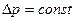и неизменной температуре фильтрата, фильтра конкретной конструкции и установленных параметров фильтровальной перегородки все входящие в уравнение фильрования величины постоянны, за исключением получаемого на фильтре объема фильтрата 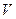и времени 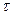. Проинтегрируем это уравнение в пределах от 0 до 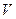и от 0 до :

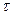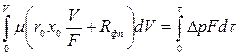
или

.

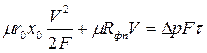Уравнение показывает зависимость продолжительности фильтрования от объема фильтрата. При решении его относительно 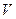можно получить зависимость объема получаемого фильтрата от продолжительности фильтрования. Это уравнение применимо к сжимаемым и несжимаемым осадкам. Постоянную разность давлений можно создавать двумя способами: или пространство над фильтровальной перегородкой сообщают с источником сжатого воздуха, или пространство под фильтровальной перегородкой присоединяют к источнику вакуума. Обычно такие процессы осуществляют в так называемых нутч-фильтрах.

В процессе фильтрования при постоянной скорости суспензию на фильтр подают поршневым насосом, производительность которого при заданном числе оборотов постоянна. В этой связи производную можно заменить отношением конечных величин и

.

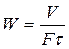Уравнение для скорости имеет вид

.

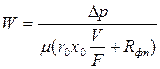Решим это уравнение относительно разности давлений 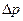, значение которой меняется с увеличением высоты осадка:

.

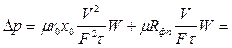
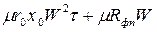Из уравнения следует, что разность давлений возрастает по мере увеличения продолжительности процесса. Это уравнение применимо к несжимаемым осадкам. При использовании его для сжимаемых осадков следует иметь аналитическую зависимость удельного сопротивления осадка от разности давлений.

Фильтрование при постоянных разности давлений и скорости осуществляется при прохождении чистой жидкости в процессе промывки осадка на фильтре способом вытеснения.

Для расчета объема промывной жидкости, подаваемой на фильтр пр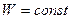и и 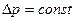, из уравнения фильтрования получим

.

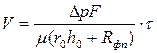Это уравнение применимо для сжимаемых и несжимаемых осадков, поскольку в процессе фильтрования .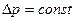

Определение постоянных в уравнениях фильтрования. К постоянным параметрам в приведенных уравнениях фильтрования относятся: 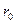, 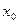и .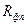

Рассмотрим один из способов их определения на примере уравнения фильтрования при постоянной разности давлений :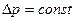

.

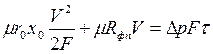Преобразуем уравнение к виду

,

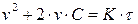где 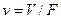- удельный объём фильтрата; 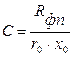- константа фильтрования, характеризующая гидравлическое сопротивление фильтрующей перегородки; 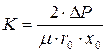- константа фильтрования, учитывающая режим процесса фильтрования и физические свойства осадка и жидкости.

Уравнение (2.18) представляется в виде

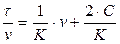. (2.19)

Уравнение (2.19) представляет собой прямолинейную зависимость между величинам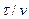и и 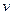. Эта зависимость может быть использована для графического определения констант и 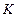. Для этой цели на оси абсцисс откладываются удельные объёмы фильтрата 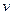(рис. 2.46), полученные на основании опытов, а по оси ординат отношения текущего времени от начала опыта к соответствующему удельному объёму фильтрата 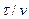. По значениям и 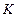вычисляют 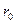и . Величину 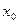определяют непосредственным измерением объемов осадка и фильтрата.

Рис. 2.46. К опытному определению констант фильтрования

С целью интенсификации фильтрования движущая сила процесса может быть значительно увеличена за счет помещения разделяемой неоднородной системы в поле центробежных сил. Фильтрование под действием центробежной силы проводится на фильтрующих центрифугах и называется центробежным фильтрованием. Барабаны центрифуг с перфорированной стенкой выкладываются изнутри мягким материалом, который выполняет роль фильтровальной перегородки. Под действием центробежной силы в массе фильтруемой суспензии развивается давление, обеспечивающее фильтрование суспензии. В результате происходит отложение осадка на внутренней поверхности барабана и удаление осветленной жидкости через фильтрующую перегородку и отверстия в барабане.

Цен­тробежное фильтрование включает в себя три периода (рис. 2.47): об­разование осадка, уплотнение осадка и механическую сушку осадка или отжима.

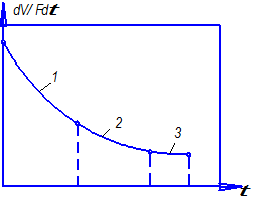
Рис. 2.47. Изменение скорости фильтрования на фильтрующих центрифугах: 1 – образование осадка; 2 – уплотнение осадка; 3 – отжим

В первом периоде происходит наиболее интенсивное удаление жидкости. Для первого периода применимы установленные выше закономерности кинетики фильтрования. Давление фильтрования определяется центробежной силой элементарного объема массой 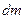, которое изменяется с радиусом барабана:

.

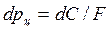
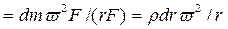Давление на фильтрующую перегородку, развиваемое всей массой суспензии в барабане, определяется интегрированием уравнения в пределах 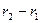(рис. 2.48):

.

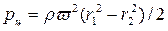Зная давление, развиваемое центробежной силой, на фильтрующую перегородку, из уравнения фильтрования для постоянной разности давлений (2.16) при замене 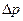на 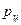можно получить зависимость для расчета времени фильтрования:

,

т.е. .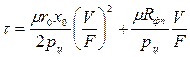

Для второго и третьего периодов центрифугирования не найдено аналитических зависимостей, с помощью которых можно получить удовлетворительные результаты. Обычно в связи с их невысокой точностью длительность процесса фильтрования определяют опытным путем.

Рис. 2.48. К расчету центробежного давления фильтрования

Date: 2015-05-09; view: 897; Нарушение авторских прав