Гидродинамическое подобие

Выше отмечалось, что дифференциальные уравнения Навье–Стокса невозможно решить для большинства технических задач.

Теория подобия позволяет преобразовать уравнения Навье–Стокса и получить из них некоторую общую функциональную зависимость между критериями подобия, характеризующими силы, действующие в потоке при движении вязкой жидкости.

Перепишем уравнение Навье–Стокса для капельной жидкости в развернутом виде для вертикальной оси :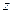

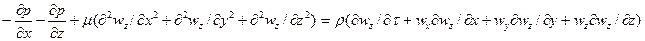Для получения безразмерных комплексов, критериев подобия, необходимо одну часть уравнения разделить на другую. Поскольку каждое из слагаемых уравнения выражает силу, действующую в потоке, то, приняв одну из них за единицу измерения – масштаб сил, безразмерные комплексы будут представлять собой соотношения сил к принятому масштабу. За масштаб сил в движущемся потоке принимается сила инерции.

Если движение жидкости установившееся, то ее скорость не зависит от времени. Член, характеризующий силу инерции после замены дифференциалов конечными величинами (операция отбрасывания знаков математических операторов), будет иметь вид

,

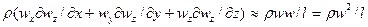где 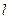– определяющий линейный размер.

Член, отражающий влияние сил тяжести на течение жидкости, равен 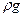. Член 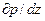, характеризующий влияние сил давления, представляется в виде

.

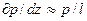Слагаемое, отражающее действие сил трения, представляется как

.

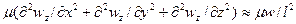Разделим члены одной части уравнения на члены другой его части и установим, таким образом, выражения, характеризующие соотношения между соответствующими силами и силой инерции.

Выражение, характеризующее отношение силы инерции и силы тяжести, называется критерием Фруда:

.

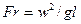Критерий Фруда отражает влияние сил тяжести, или собственного веса, на движение жидкости. Представляет собой меру отношения силы инерции к силе тяжести в подобных потоках.

Соотношение между силами давления и инерции представляет собой критерий Эйлера:

.

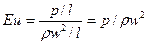Обычно критерию Эйлера придают иной вид, введя в него вместо абсолютного давления разность давлений 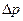между двумя какими-либо точками жидкости:

.

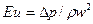Критерий Эйлера отражает влияние перепада гидростатического давления на движение жидкости. Его величина характеризует отношение изменения силы гидростатического давления к силе инерции в подобных потоках.

Безразмерный комплекс, являющийся отношением инерционных сил к силам трения в подобных потоках, представляет известный нам критерий Рейнольдса:

.

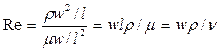Величина 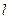в критерии Рейнольдса, как и в других критериях подобия, представляет определяющий линейный размер. При движении жидкости через трубопроводы или аппараты за этот размер принимается диаметр, а в случае некруглого сечения потока – эквивалентный диаметр .

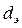При неустановившемся течении жидкости в уравнении Навье–Стокса 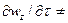0. Преобразуем слагаемое, отражающее влияние нестационарности течения, 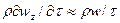. Безразмерный комплекс, полученный отношением силы инерции к члену уравнения, отражающему нестационарный процесс, называется критерием гомохронности:

,

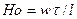Критерий гомохронности учитывает неустановившийся характер движения жидкости в подобных потоках.

Во всех сходственных точках подобно движущихся потоков жидкости критерии подобия равны (одни и те же – ), т.е. , , , .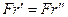

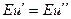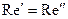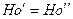Согласно второй теореме подобия, решение уравнений Навье - Стокса можно представить в виде функциональной зависимости между полученными критериями подобия, т.е.

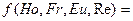0,

или после добавления симплексов геометрического подобия, представляющих собой отношение одноименных геометрических размеров, характеризующих реальный объект и модель, к определяющим получим

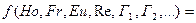0,

где 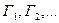- симплексы геометрического подобия.

Все критерии в критериальном уравнении самого общего вида, кроме критерия Эйлера, являются определяющими, т.к. они составлены исключительно из величин, входящих в условия однозначности. В критерий Эйлера входит разность давлений 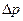, величина которой при движении жидкости по трубе определяется формой трубы (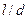), физическими свойствами жидкости () и распределением скоростей у входа в трубу и у ее стенок (начальные и граничные условия). Поэтому, согласно третьей теореме подобия, для подобия двух систем необходимо и достаточно соблюдения равенства значений 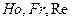и симплексов геометрического подобия. Следствием выполнения этих условий будет равенство значений определяемого критерия 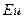в сходственных точках подобных потоков. Поэтому критериальное уравнение общего вида представляют в виде зависимости определяемого критерия от определяющих критериев:

.

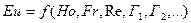Зависимости подобного вида называют обобщенными или критериальными уравнениями гидродинамики.

Как уже было сказано выше, подобные функции наиболее удобно апроксимировать степенными зависимостями вида

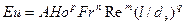
или после подстановки соответствующих комплексов величин

.

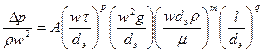Если движение жидкости является стационарным, то критерий 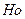может быть исключен из уравнения. Поэтому для установившегося течения жидкости обобщенное уравнение гидродинамики будет иметь вид

.

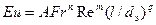Модифицированные критерии подобия. В ряде случаев оказывается затруднительным или даже невозможным определить или вычислить ту или иную физическую величину, входящую в критерий подобия. Тогда эту величину исключают путем сочетания двух или более критериев. В результате такой операции получают так называемый производный критерий подобия. При этом исключенную величину обычно заменяют на другую, ей пропорциональную, опытное или расчетное определение которой является наиболее простым.

Так, например, в процессе теплообмена в условиях естественной конвекции, возникающей под действием разности плотностей жидкости, обусловленной различием температур в разных ее точках, трудно определить скорость конвективных токов. Однако эта скорость входит в критерий Фруда, отражающий подобие таких процессов. Поэтому неизвестная скорость в процессе может быть исключена путем сочетания критериев Рейнольдса и Фруда:

.

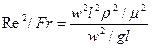Полученный комплекс величин является производным критерием, называемым критерием Галилея:

.

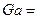
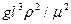Можно получить другой производный критерий – критерий Архимеда, представляющий собой критерий Галилея, умноженный на симплекс физического подобия–безразмерную плотность:

.

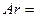
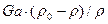
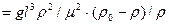Если заменить симплекс 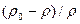пропорциональной ему относительной разностью температур, то можно получить новый производный критерий, являющийся критерием теплового подобия Грасгофа.

Соблюдение равенства критериев 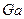или является необходимым при моделировании различных процессов, протекающих под действием силы тяжести.

Date: 2015-05-09; view: 686; Нарушение авторских прав