Основные характеристики движения жидкостей

Гидравлический радиус и эквивалентный диаметр. При движении жидкости через площадь поперечного сечения любой формы, отличающейся от круглой, в качестве расчетного линейного размера применяют гидравлический радиус или эквивалентный диаметр.

Гидравлический радиус 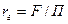представляет собой отношение площади поперечного сечения трубы или канала, через которое протекает жидкость, к смоченному периметру.

Для круглой трубы:

.

Диаметр, выраженный через гидравлический радиус, представляет собой эквивалентный диаметр

,

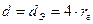следовательно

.

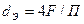Эквивалентный диаметр равен диаметру гипотетического трубопровода круглого сечения, для которого отношение площади F к смоченному периметру П то же, что и для заданного трубопровода некруглого сечения.

Для квадрата со сторонами a и b эквивалентный диаметр равен:

.

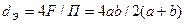Для кольцевого сечения с внутренним диаметром D большого трубопровода и наружным малого d:

.

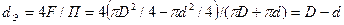Для круглой трубы:

.

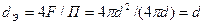Установившиеся и неустановившиеся потоки. Движение жидкости называется установившимся или стационарным, если скорости частиц потока и другие параметры, влияющие на его движение, например, 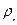, р, Т, не изменяютсяво времени в каждой фиксированной точке пространства. Расходы жидкости при установившемся течении через поперечные сечения канала также не зависят от времени.

При установившемся движении жидкости проекция скорости 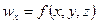, может быть переменной в любой из точек 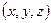, но не меняется со временем, т.е. .

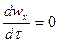В отличие от стационарного при неустановившемся или нестационарном потоке факторы, влияющие на движение жидкости, изменяются во времени

, т.е. .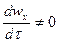

Установившиеся условия движения жидкости характерны для непрерывных процессов химической технологии. Неустановившееся течение жидкости происходит главным образом в периодических процессах или возникает кратковременно в непрерывных процессах в период пуска или изменения режима работы установки.

Для каждой движущейся частицы жидкости изменение ее параметров во времени и пространстве выражается не частной, а полной производной во времени, называемой в гидродинамике субстанциональнойпроизводной. По смыслу ее называют производной, следующей за потоком.

Обозначим через 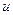любую величину, изменяющуюся в потоке жидкости как во времени, так и в пространстве, например: плотность, давление, температуру, концентрацию или любую из составляющих скорости 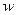жидкости в направлении осей координат .

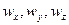Допустим, что при наблюдении за движением потока можно мгновенно регистрировать значение параметра 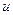в каждый момент времени и в любой точке потока. Изменение параметра 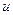в единицу времени для фиксированной точки пространства 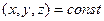выражается частной производной 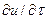, а изменение 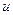в указанной точке за бесконечно малый промежуток времени 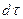составляет 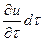. Это изменение является местным или локальным изменением данной переменной. При установившемся движении .

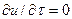Если наблюдатель перемещается вместе с потоком, с какой–либо частицей, то за время 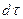частица потока переместится из точки А с координатами 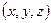в точку В с координатам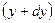и , и .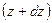

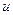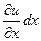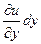В результате перемещения из точки А в точку В изменения , соответствующие проекциям пути , равны , и 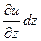. Эти изменения не связаны с изменением 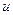во времени в какой–либо фиксированной точке пространства. Если бы не было локального изменения 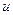, то при переходе частицы из точки А в точку В значение 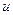изменилось бы на величину

.

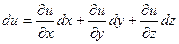Это выражение представляет собой конвективное изменение параметра .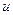

Полное изменение 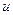при неустановившемся движении представляет собой сумму локального и конвективного изменений:

,

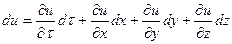откуда изменение параметра за малый промежуток времени:

,

, , ,

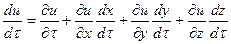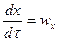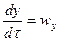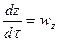тогда

.

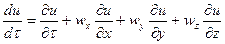При установившемся движении ,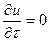

.

Последние выражения представляют собой субстанциональную производную для неустановившегося и установившегося течения жидкости. Они характеризуют изменение какого–либо параметра или свойства материи (субстанции) во времени при перемещении материальных частиц в пространстве. С учетом специфики понятия субстанциональную производную зачастую обозначают 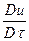вместо .

Уравнение неразрывности (сплошности) потока. Представляет собой зависимость между скоростями в потоке жидкости, для которого соблюдается условие сплошности, или неразрывности течения, т.е. не образуется пустот, не заполненных жидкостью.

Уравнение выражает фундаментальный закон сохранения массы (расхода).

Дифференциальное уравнение неразрывности для неустановившегося течения имеет вид

.

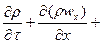
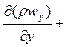
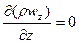В установившемся потоке плотность не меняется во времени 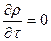, поэтому уравнение неразрывности выглядит так:

.

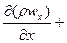
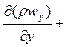
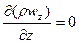Для капельных жидкостей, которые практически несжимаемы, а также для газов в условиях изотермического потока, при скоростях меньших скорости звука, 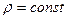, следовательно, уравнение неразрывности примет вид

.

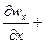
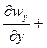
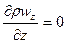Для трубопровода постоянного сечения в результате интегрирования дифференциального уравнения неразрывности для установившегося однонаправленного движения жидкости (в направлении оси 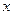) получается зависимость

.

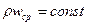Если же площадь сечения трубопровода переменна, то интегрирование по площади приводит к зависимости

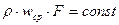. (2.4)

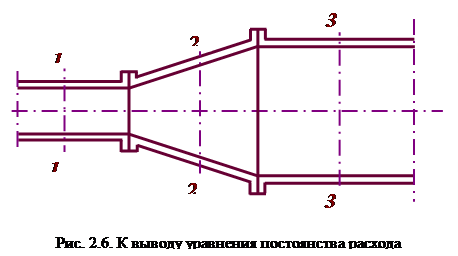
Для трех сечений трубопровода одного и того же потока жидкости (рис.2.6).

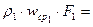
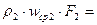
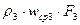
или для массового расхода жидкости в трубопроводе переменного сечения

.

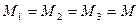Согласно уравнению постоянства расхода, при установившемся течении жидкости, полностью заполняющей трубопровод, через каждое его поперечное сечение проходит в единицу времени одно и то же количество жидкости.

,

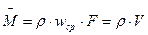при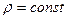

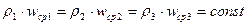(2.5)

или для объемного расхода жидкости в трубопроводе переменного сечения

.

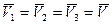Из уравнения (2.5) следует, что скорости капельной жидкости в различных поперечных сечениях трубопровода обратно пропорциональны площадям этих сечений.

В соответствии с уравнением (2.4), массовый расход жидкости через начальное сечение трубопровода равен ее расходу через конечное сечение трубопровода. Таким образом, уравнение неразрывности является частным случаем закона сохранения массы и выражает материальный баланс потока.

Скорость и расход жидкости. Количество жидкости, протекающей через поперечное сечение потока в единицу времени, называется расходом жидкости.

Различают объемный (м³/с) и массовый (кг/с) расходы.

В разных точках поперечного сечения потока скорости частиц жидкости неодинаковы, поэтому в расчетах используют не истинные (локальные) скорости, а фиктивную среднюю скорость:

.

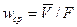Объемный расход жидкости равен:

,

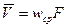массовый расход – ,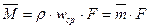

массовая скорость жидкости – .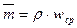

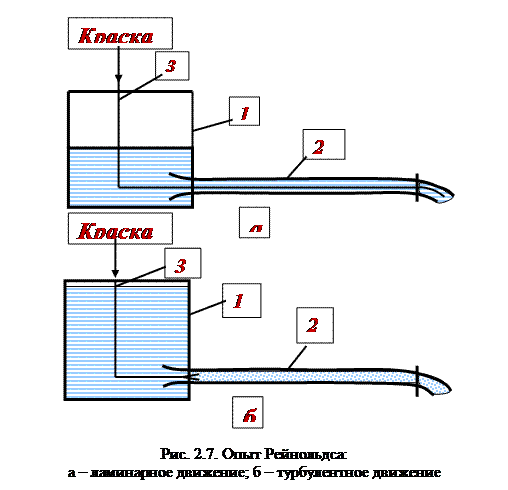
Режимы движения жидкостей. Характер движения жидкости зависит от скорости ее течения. Этот вопрос был решен в 1883 г. О. Рейнольдсом, который поставил простой убедительный опыт. Установка О. Рейнольдса показана на рис. 2.7. Характер движения жидкости устанавливается по степени размытости струйки подкрашенной жидкости, истекающей по трубке 2 из сосуда 1. В зависимости от высоты уровня жидкости в сосуде 1, устанавливалась та или иная скорость течения.

При малых скоростях течения струя окрашенной жидкости 3 не размывалась, что указывало на послойный характер движения жидкости. Такие течения были названы ламинарными.

При некоторой критической скорости струйка размывалась по всему сечению, что свидетельствовало о вихревом характере перемешивания жидкости по всему сечению трубы 4. Такой режим течения был назван турбулентным. Рейнольдс показал, что переход от одного режима течения к другому соответствует определенному значению безразмерной величины:

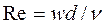
где 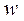– средняя скорость; 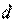– диаметр канала; 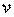– кинематический коэффициент вязкости жидкости.

Безразмерная переменная впоследствии был названа числом или критерием Рейнольдса. Переход от ламинарного течения наступает при 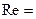2300. При 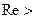2300 чаще всего наблюдается турбулентный режим течения. Однако при 2300 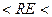10000 режим течения неустойчиво турбулентный, или переходный.

Вышесказанное справедливо к стабилизированным изотермическим потокам в прямых трубах с малой шероховатостью стенок. Наличие различных возмущений, обусловленных шероховатостью стенок трубы, изменением скорости или направления течения потока, близость входа в трубу и т. п. могут существенно снизить значения критических чисел Рейнольдса.

Распределение скоростей в движущемся потоке жидкости. Распределение скоростей определяется режимом течения жидкости. При ламинарном режиме распределение может быть установлено законом Стокса:

,

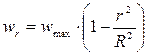представляющим параболическое распределение скоростей в сечении трубопровода, где 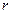– текущий радиус, отсчитываемый от оси трубопровода; 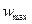– скорость на оси трубопровода.

Средняя скорость по сечению трубопровода связана с максимальной скоростью следующим соотношением:

.

Уравнение, определяющее объемный расход жидкости при ее ламинарном движении в круглой прямой трубе, носит название уравнения Пуазейля:

.

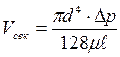Date: 2015-05-09; view: 1318; Нарушение авторских прав