Движение жидкостей через неподвижные пористые слои

Во многих процессах пищевых производств имеет место движение жидкостей и газов через неподвижные зернистые и пористые слои.

Форма и размеры элементов зернистых слоев весьма разнообразны: частицы слоев осадка на фильтрах, гранулы, таблетки, кусочки катализаторов или адсорбентов, насадочные тела абсорбционных и ректификационных колонн. При этом зернистые слои могут быть монодисперсными или полидисперсными в зависимости от того, одинаковы или различны по размеру частицы зернистого слоя.

При движении жидкостей или газов через зернистый слой можно считать, что поток одновременно обтекает отдельные элементы слоя и движется внутри каналов неправильной формы, образуемых пустотами и порами между элементами. Изучение такого движения, как указывалось выше, представляет смешанную задачу гидродинамики.

При расчете гидравлического сопротивления зернистого слоя может быть использована зависимость, аналогичная по виду для расчета потерь давления на трение в трубопроводах:

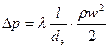. (2.8)

Коэффициент 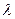в уравнении (2.8) учитывает не только влияние сопротивления трения, но и дополнительные местные сопротивления, появляющиеся при движении жидкостей и газов по искривленным каналам в слое и обтекании его отдельных элементов.

Эквивалентный диаметр, соответствующий суммарному поперечному сечению каналов в зернистом слое, может быть определен следующими характеристиками слоя.

Удельной поверхностью 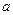, представляющей собой поверхность элементов, или частиц материала, находящихся в единице объема, занятого слоем.

Долей свободного объема, или порозностью 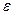, представляющей собой отношение объема свободного пространства между частицами 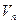к объему всего слоя 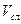, т.е. .

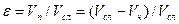Эквивалентным диаметром

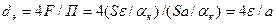, (2.9)

где 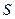- площадь сечения аппарата, заполненного зернистым слоем;

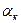- коэффициент кривизны каналов по толщине зернистого слоя.

Эквивалентный диаметр может быть выражен также через размер частиц, составляющих слой. Пусть в 1 м³ объема, занимаемого слоем, имеется 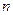частиц. Объем самих частиц составляет (1- 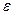), а их поверхность равна .

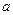Средний объем одной частицы равен:

,

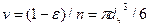ее поверхность

,

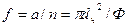где 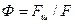- фактор формы частицы, представляющий отношение поверхности шара 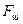, имеющего тот же объем, что и рассматриваемая частица с поверхностью 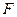. Для шарообразной частицы 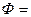1.

Отношение поверхности частицы к ее объему

,

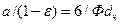откуда

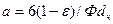. (2.10)

Подставим значение 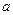в уравнение (2.9) и получим зависимость для расчета эквивалентного диаметра зернистого слоя через размер частиц:

.

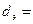
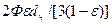В уравнение (2.8) входит действительная скорость жидкости (газа) в каналах слоя, которую определить сложно. Наиболее целесообразно выразить ее через скорость, условно отнесенную к полному поперечному сечению слоя или аппарата. Эту скорость, равную отношению объемного расхода жидкости к площади поперечного сечения слоя, называют фиктивной скоростью .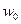

Соотношение между действительной и фиктивной скоростями следующее:

.

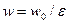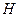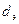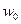Подставив в уравнение (2.8) вместо длины канала высоту слоя , выражения для и , получим

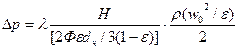
или

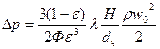. (2.11)

Величина коэффициента сопротивления зависит от гидродинамического режима, определяемого критерием Рейнольдса, который в соответствии с принятыми обозначениями примет вид

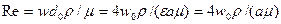. (2.12)

При замене в уравнении (2.11) удельной поверхности 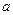ее значением из формулы (2.10) получим

,

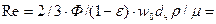
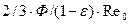где 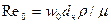- модифицированный критерий Рейнольдса, выраженный через фиктивную скорость жидкости (газа) и размер частиц слоя.

Для расчета коэффициента сопротивления для всех режимов течения рекомендовано обобщенное уравнение следующего вида

.

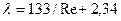Для ламинарного режима течения (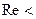 50):

.

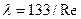Подставим зависимости для 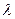и критерия в выражение (2.11) и после преобразования получим

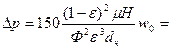
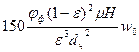, (2.13)

где 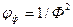- коэффициент формы.

Уравнение (2.13) может быть использовано для расчета удельного сопротивления осадка в процессе фильтрования. Его также применяют для экспериментального определения фактора 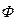или коэффициента формы 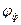частиц зернистого слоя. Опыты проводят при ламинарном режиме течения жидкости (газа). Их не сложно осуществить путем измерения сопротивления слоя 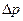, определения фиктивной скорости 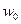при известных значениях вязкости жидкости (газа) и других параметрах зернистого слоя.

Date: 2015-05-09; view: 672; Нарушение авторских прав