Теплообмен при ламинарном течении конденсата на вертикальной стенке

Рассмотрим процесс конденсации сухого насыщенного пара с постоянными физическими свойствами на вертикальной стенке (рис.10.5) при следующих допущениях:

- течение установившееся, ламинарное;

- в пленке силы инерции и давления малы, по сравнению с силами вязкости и силами тяжести;

- трением и поверхностным натяжением на границе конденсата и пара можно пренебречь;

- температура стенки Т_с и конденсата на внешней поверхности пленки Т_п = Т_н - постоянные величины;

- конвективный перенос тепла в пленке и теплопроводность вдоль оси х пренебрежимо малы, по сравнению с переносом тепла к стенке 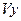.≤ 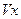, δ ≤ α

Уравнение движения в проекции на ось x и уравнение энергии

,

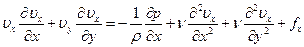
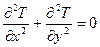где ; ;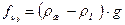

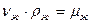
при сделанных допущениях существенно упрощаются и приобретают вид:

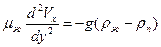(10.20)

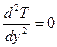(10.21)

граничные условия:

при y = 0, T = T_с, V_x = 0; (10.22)

при y = d, T = T_н, 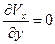; (10.23)

интегрирую уравнение (10.20) получим:

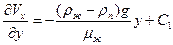(10.24)

и

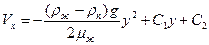(10.25)

где постоянные интегрирования находятся из граничных условий (10.22), (10.23)

y = 0, 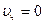; C₂ =0

;

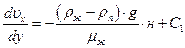
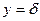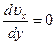
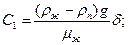
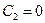(10.26)

и

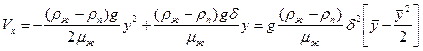(10.27)

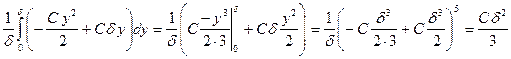
где .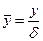

Средняя скорость 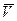в сечении x:

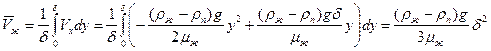(10.28)

Локальный, отнесенный к единице площади, тепловой поток на участке [x,x+dx] равен:

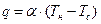(10.29)

Из уравнения (10.21) и граничного условия (10.22):

, , , , , , ;

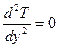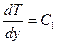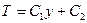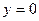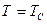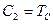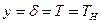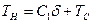
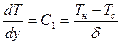
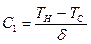(10.30)

и

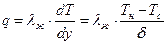(10.31)

Из сопоставления выражений (10.29) и (10.31) получаем:

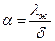(10.32)

Из уравнений (10.19), (10.28) и (10.31) получаем дифференциальное уравнение относительно d(x):

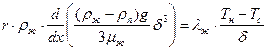(10.33)

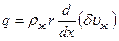
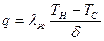или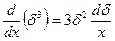

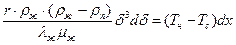(10.34)

Проинтегрировав уравнение (10.34) от x = 0 до x получим:

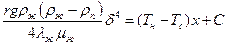(10.35)

где из условия x = 0, d = 0, следует C = 0 и

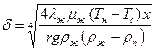(10.36)

Из соотношений (10.32) и (10.36) получим формулу для определения локального коэффициента теплоотдачи (впервые она получена В. Нуссельтом в 1916г.)

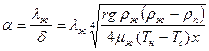(10.37)

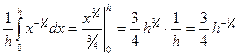
Средний на длине пластины h коэффициент теплоотдачи равен:

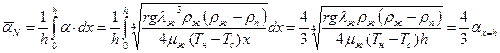(10.38)

Из соотношения (10.36) следует, что толщина пленки увеличивается при изменении x по зависимости:

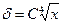(10.39)

где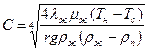

Коэффициент теплоотдачи (10.32), (10.37) уменьшается с увеличением x, вследствие увеличения толщины пленки d и термического сопротивления .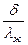

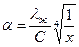(10.40)

Увеличение температурного напора 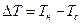приводит к росту удельного теплового потока, как это следует из (10.29) и (10.37)

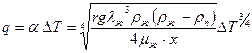(10.41)

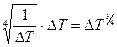
Как показали результаты расчетов Г.Н. Кружилина и Д.А. Лабунцова, учет сил инерции в уравнении (10.20) и конвективного переноса тепла в уравнении (10.21) не вносит уточнений при условии 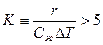, где К – критерий С.С. Кутателадзе, и 1£Pr£100. Вне этого диапазона коэффициент теплоотдачи a умножают на поправочный множитель .

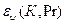Учет переменности физических параметров конденсата может быть проведен введением поправки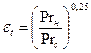

В случае волнового режима периодического движения пленки, как установил П.Л. Капица, средний коэффициент теплоотдачи возрастает на 21% Д.А. Лабунцов показал, что при беспорядочном волновом движении в пленке коэффициент теплоотдачи увеличивается пропорционально 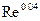и 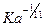, где критерий Капицы, учитывающий соотношения сил поверхностного натяжения, тяжести и вязкости, 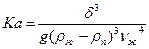, и приближенно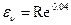

Таким образом, средний коэффициент теплоотдачи при ламинарном режиме движения пленки конденсата на вертикальной стенке может рассчитываться по формуле:

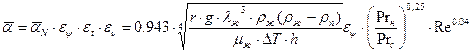(10.42)

Уравнение (42) может быть записано в безразмерном критериальном виде:

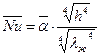
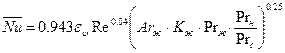(10.43)

где , , , .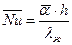

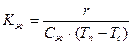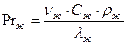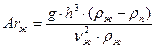Число Кутателадзе для ж.

Если r_п <<r_ж, то в формуле (10.43) вместо числа Архимеда Ar, используется число Галилея .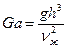

При К≥5, 1≤Pr_ж≤100e_y, (e_y= 1), 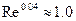, , 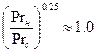формула (10.43) упрощается и приобретает вид:

(10.44)

Date: 2015-05-09; view: 759; Нарушение авторских прав