Необратимость при расширении газа в вакуум

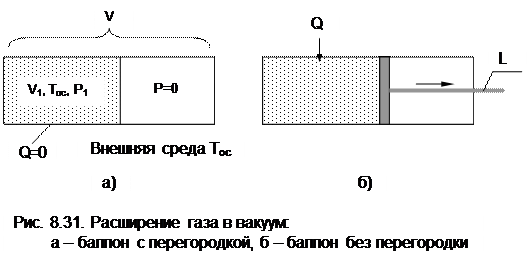
Рассмотрим жесткий сосуд, имеющий объем V и разделенный перегородкой на две части (рис.8.31, а). Одну часть сосуда с объемом V₁ занимает газ при температуре Т_ос, равной температуре окружающей среды, в другой части сосуда – абсолютный вакуум. Поскольку газ и окружающая среда имеют одинаковые температуры, такая термодинамическая система находится в равновесном состоянии. Если убрать перегородку (рис.8.31, б), произойдет расширение газа в вакуум, в результате чего газ займет весь объем сосуда V. Это типичный необратимый процесс, сопровождающийся увеличением энтропии системы и потерей возможной работы (эксергии).

Поскольку процесс расширения газа быстротечен, считаем, что теплообмен газа с окружающей средой отсутствует, т.е. Q=0. При расширении газа объем сосуда не изменяется и механической работы он не совершает, т.е. L=0. В соответствии с первым законом термодинамики (Q=U₂-U₁+L) при Q=0 и L=0 изменения внутренней энергии газа в такой системе нет, т.е. U₂=U₁. Применительно к идеальному газу нет и изменения температуры в такой системе, Т₂=Т₁. Таким образом, изменение энтропии системы равно изменению энтропии газа, т.к. теплообмен газа с окружающей средой отсутствует, а изменение энтропии идеального газа может быть рассчитано по изотермическому процессу в виде выражения

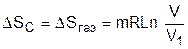. (8.42)

Поскольку при расширении газа его объем увеличивается, то в соответствии с уравнением (8.42) энтропия системы возрастает.

Определить потерю максимально возможной работы (эксергии) при расширении идеального газа в вакуум можно, заменив в нашей системе перегородку поршнем со штоком (рис.8.31, б) осуществив обратимое изотермическое расширение газа. Таким образом, газ будет совершать такой же изотермический процесс, как и в первом случае, но на штоке поршня будет получена полезная механическая работа. В соответствии с первым законом термодинамики применительно к газу эта работа равна теплоте (L=Q), поскольку изменения внутренней энергии идеального газа в изотермическом процессе расширения нет. Рассчитать эту работу можно по формуле изотермического процесса:

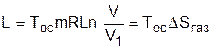. (8.43)

В соответствии с первым законом термодинамики для всей термодинамической системы эта работа должна быть равна теплоте, полученной газом в обратимом процессе изотермического расширения от окружающей среды, т.е. -Q_ос=Q=L. Другими словами, полезная работа в нашей системе была получена за счет подвода теплоты к газу от внешней среды. При осуществлении такого расширения газа в вакуум энтропия окружающей среды уменьшится на такую же величину, на какую увеличится энтропия газа:

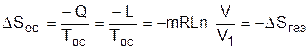, (8.44)

т.е. изменение энтропии в нашей системе

ΔS_c = ΔS_газ + ΔS_оc = 0,

следовательно, в ней протекают только обратимые процессы.

В случае полностью необратимого расширения газа в вакуум вся возможная полезная работа (8.43) теряется. Оценить потерю этой работы, как любого необратимого процесса, позволяет теорема Гюи–Стодолы, выражение которой получается из уравнений (8.42) и (8.43):

.

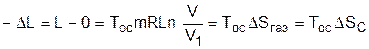Date: 2015-05-09; view: 1021; Нарушение авторских прав