Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?
Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника
С одинаковыми температурами и давлениями
|
|
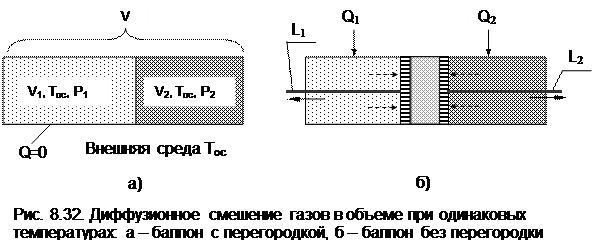
Смешение двух различных газов, имеющих одинаковые температуры и давления, это тоже необратимый процесс. Рассмотрим такой процесс на примере двух различных газов, находящихся в сосуде объемом V, разделенном перегородкой на две части с объемами V1 и V2 (см. рис.8.32, а). В этих частях сосуда находятся разные газы при одинаковых давлениях P и температурах, равных температуре окружающей среды Tос. Для упрощения анализа процесса смешения будем считать, что оба газа идеальные.
Если убрать перегородку, то произойдет типично необратимый процесс диффузионного смешения газов с возрастанием энтропии системы. В соответствии с законом Дальтона каждый газ при расширении ведет себя так, как будто другого газа в сосуде нет. При этом в конце процесса смешения каждый газ будет занимать весь объем сосуда V, а парциальные давления газов будут определяться выражениями
.
 |
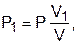
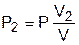Как и при расширении в вакуум, диффузионное смешение газов в нашем примере будет происходить без теплообмена с окружающей средой (Q=0) и без совершения работы изменения объема (L=0). Следовательно, в соответствии с первым законом термодинамики изменения внутренней энергии в нашей системе нет (Uсм-(U1+U2)=0). Поскольку внутренняя энергия идеального газа зависит только от температуры, а температура обоих газов до смешения была одинакова, то и после смешения температура газа останется прежней, т.е. наш процесс смешения будет изотермическим.
Изменение энтропии в такой системе будет соответствовать изменению энтропии газов, поскольку теплообмен газов с окружающей средой отсутствует. Рассчитать изменение энтропии системы можно по формулам изотермических процессов расширения для каждого газа:
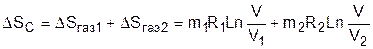. (8.45)
Очевидно, что в процессе диффузионного смешения газов энтропия системы возрастает.
Для того чтобы оценить потерю возможной работы в диффузионном процессе смешения газов, проведем теоретически обратимый процесс диффузионного смешения газов. Для этого заменим перегородку в сосуде с газами двумя полупроницаемыми поршнями со штоками (см. рис.8.32, б). Левый поршень проницаем только для первого газа, а правый поршень – только для второго газа. В результате такого процесса смешения между поршнями образуется смесь газов. При этом на левый поршень действует справа давление (парциальное) только второго газа, на правый поршень действует слева давление (парциальное) первого газа. Поршни будут двигаться в противоположных направлениях, передавая через штоки полезную работу L1 и L2 в окружающую среду.
В соответствии с первым законом термодинамики для всей термодинамической системы эти работы должны быть равны теплоте, полученной каждым газом в обратимых процессах их теплообмена с окружающей средой при осуществлении процесса смешения, т.е. L1=Q1 и L2=Q2. Следовательно, внутренняя энергия каждого газа и всей системы в процессе смешения не изменится, а так как температуры газов одинаковы, то обратимый процесс диффузионного смешения газов будет изотермическим. Работу такого изотермического расширения газов можно рассчитать по формуле
. (8.46)
Date: 2015-05-09; view: 795; Нарушение авторских прав