Политропный процесс

Политропным процессом называется такой термодинамический процесс изменения состояния физической системы, при котором в течение всего процесса сохраняется постоянство теплоемкости.

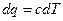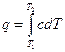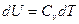Пусть С – теплоемкость политропного процесса, тогда используя выражения или ; и 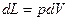, получим уравнение первого закона термодинамики в виде:

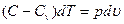. (92)

С учетом выражения 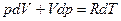после ряда преобразований имеем:

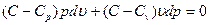, (93)

откуда получим уравнение политропы:

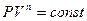, (94)

где 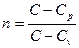– показатель политропы.

Согласно определению политропного процесса n может быть любым, но постоянным в некотором интервале числом, которое достаточно близко воспроизводило бы разнообразные встречающиеся в практике линии индикаторных диаграмм.

Очевидно, что при некоторых частных значениях n уравнение (94) должно превращаться в уравнения простейших термодинамических процессов.

20 Действительно, если в уравнении (94) n = 0, получим уравнение изобары:

.

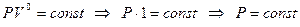В этом случае (для изобарного процесса) уравнение первого закона термодинамики для изолированных систем будет совпадать с формулой (49).

При 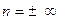получим уравнение изохоры:

,

поскольку величина 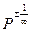будет бесконечно мала по сравнению с объемом (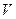), ею можно пренебречь, тогда:

.

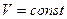22 Из определения изохорного процесса очевидно, что работа в этом процессе не совершается, поскольку работа есть произведение 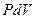(работа всегда связана с изменением объема). Тогда уравнение первого закона термодинамики для изолированных систем (49) при изохорном процессе примет вид:

. (95)

Таким образом, подведенная к изолированной системе теплота в изохорном процессе расходуется только на изменение внутренней энергии системы.

При 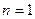получим уравнение изотермы:

,

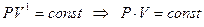но поскольку, согласно закону Бойля – Мариотта, если произведение давления и объема есть величина постоянная, то процесс – изотермический, тогда:

.

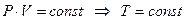21 В изотермическом процессе не происходит изменения внутренней энергии системы, поскольку температура постоянна. Тогда уравнение первого закона термодинамики для изолированных систем (49) при изотермическом процессе примет вид:

. (96)

Таким образом, подведенная к изолированной системе теплота в изотермическом процессе расходуется только на совершение системой внешней работы.

При 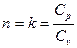получим уравнение адиабаты:

.

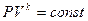23 Показатель адиабаты 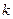еще называют коэффициентом Пуассона. Величина этого показателя зависит от числа атомов в молекуле газа. При этом 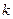может принимать следующие значения:

· для одноатомных газов (на самом деле состояние одноатомного газа не существует, оно введено для идеальных газов) ;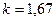

· для двухатомных газов (CO; О₂; N₂; Н₂; F₂; Cl₂; воздух и др.) ;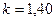

· для трехатомных газов (CO₂; N₂O; NO₂ и др.) .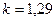

По определению, адиабатный процесс – это процесс, протекающий без теплообмена с окружающей средой, т.е. 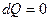. Тогда уравнение первого закона термодинамики для изолированных систем (49) при адиабатном процессе примет вид:

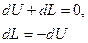(97)

Таким образом, в адиабатном процессе работа может совершать за счет изменения (уменьшения) внутренней энергии системы в течение некоторого времени.

Таким образом политропный процесс является обобщающим по отношению к простейшим процессам. Для политропы справедливы соотношения:

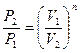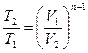; ; . (98)

Работу политропного процесса можно определить по следующим формулам:

; ; ;

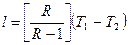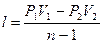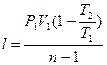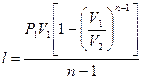; . (99)

В PV -координатах работа l характеризуется площадью под процессом. Если то и 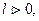верно и обратное.

Теплоемкость политропного процесса можно определить по формуле:

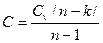. (100)

Таким образом, еще раз подтверждается, что теплоемкость идеального газа зависит от характера термодинамического процесса, что наглядно подтверждается на рисунке 7.

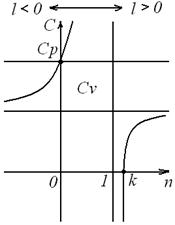
Рисунок 7 – Зависимость теплоемкости С процесса от показателя п политропы

На рисунке 8 представлены совмещенные диаграммы различнох термодинамических процессов.

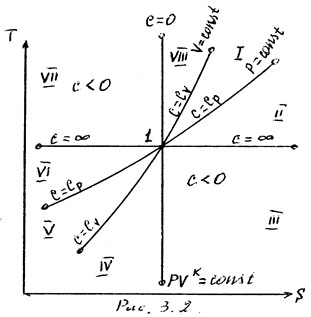
Рисунок 8 - Совмещенные диаграммы различных термодинамических

процессов в PV- и TS – координатах

Если в РV- и ТS – координатах выбрать некоторую произвольную точку 1 и провести из нее все рассмотренные выше термодинамические процессы, то все поле построенной таким образом диаграммы делится на 8 областей, характеризующихся определенными признаками. Так, все процессы слева от точки 1 на РV – диаграмме сопровождаются отрицательной работой. Все процессы справа от точки 1 на TS – диаграмме происходят с подводом теплоты, слева – с отводом теплоты, вверх от изотермы – с увеличением внутренней энергии и энтальпии; вниз – с уменьшением. Области, выделенные на PV – диаграмме, соответствуют процессам с подводом теплоты, а на ТS – диаграмме – процессам с положительной теплоемкостью и т.д.

Для определения изменения энтропии в политропном процессе достаточно уравнение (100) подставить в выражение 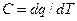, и с учетом того, что 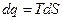получим:

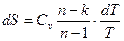. (101)

После интегрирования:

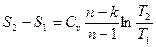. (102)

С учетом выражений (98), можно записать:

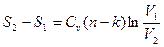. (103)

Изменения внутренней энергии и энтропии в политропном процессе определяются в ТS – координатах площадями соответственно под изохорным и изобарным процессами, происходящими в том же интервале температур .

Date: 2015-05-09; view: 3048; Нарушение авторских прав