Графические модели. равнонаклонённых плоскостей и их позиционные свойства

равнонаклонённых плоскостей и их позиционные свойства

К числу позиционных особенностей не-которых плоскостей общего положения от-носится их равнонаклонённост ь к разным плоскостям проекций.

Определение 9.9. Плоскости общего положения, составляющие метрически равные углы наклона к разноименным пло-скостям проекций, называются равнона-клонёнными.

Конструктивно они могут быть двух ви-дов: положительно (рис.9.31) и отрица- тельно равно наклоненными (9.32).

У первых одинаковые углы j ° между линиями u и v наибольшего уклона к П₁ и П₂ и их проекциями на эти плоскости распо-ложены по одну от них сторону, а у вторых, - по разные стороны. Равнонаклонённость этих плоскостей к П₁ и П₂ определя-ет изобразительные свойства их зада- ния следами (или линиями уровня) на 2-х и 3-х картинном комплексном черте- же (рис 9.33 -- 9. 35).

Утверждение 9.16.: Если плоскость a по- ложительно равнонаклонена к П₁ и к П₂, то её гори зональный h°₁ и фронталь-ный f°₂ следы равнонаклонённы к оси х_12, а профильный след р°₃ параллелен постоянной прямой k₁₂₃ трёхкартинного комплексного чертежа.

Из рис.9.31 видно, что треугольник сле-дов U₁₂ V₁₃ W₂₃ является равнобедренным. Его основанием служит профильный р°₃ след плоскости a, который параллелен профильному следу d°₃ биссекторной плос-кости d, откуда следует, что плоскость a пересекает эту биссекторную плоскость по её профильной линии уровня m_d, прохо-дящей через точку U₁₂ схода следов плос-кости a.

Утверждение 9.17. Если плоскость a отрицательно равнонаклонена к П₁ и к П₂, то её горизонтальный и фронтальный следы являются продолжением друг дру-га, а профильный след перпендикулярен к постоянной прямой k₁₂₃ трёхкартинного комплексного чертежа.

Из рис. 9.32 видно, что треугольник следов U₁₂ V₁₃ W₂₃ является равнобед-ренным, а линия пересечения плоскости a с биссекторной плоскостью d является биссектрисой острого угла между её гори-зонтальным и фронтальным следами.

Таким образом, равнобедренность тре-угольника следов плоскости a является графическим признаком её равнонакло-нённости к тем плоскостям проекций, с которыми она пересекается по его равным сторонам. При этом положение основания треугольника следов по отношению к пос-тоянной прямой k₁₂₃ говорит о характере равнонаклонённости (положительная или отрицательная) и о плоскостях проекций, к которым она осуществляется (рис.9.35):

1. p°₃ || k₁₂₃ Þ a ^ П₁ = a^П₂;

2. h°₁ || k₁₂₃ Þ a^П₂ = a^П_{3 ;}

3. f°₂ ^ k₁₂₃ Þ a^П₁ = a^П_{3 .}

Если равные между собой отрезки сле-

дов р°₃, h°₁ и f°₂ привести в состояние пе-ресекаемости на осях х₁₂, у₁₃ и z₂₃, то они образуют равносторонний треугольник сле-дов плоскости a, равнонаклонённый к трём плоскостям проекций (рис. 9.36).

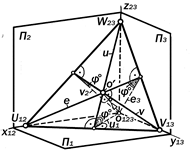
Рис. 9.36. Плоскость, равнонаклонённая к трём плоскостям проекций.

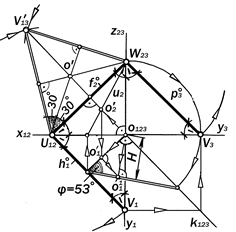
Рис 9.37.. Графическая модель плоскости, равнонаклонённой к трём плоскостям проекций

Такая плоскость единственна. Её конст-руктивной особенностью является совпа-дение линий наибольших уклонов u, v, e к плоскостям проекций П₁, П₂ и П₃ с высота-ми, медианами и биссектрисами треуголь-ника следов, точкой О¢ пересечения кото-рых является основание перпендикуляра, опущенного из начала координат О₁₂₃ на плоскость a. Длина Н этого перпендикуляра определя- ет высоту пирамиды О₁₂₃ U₁₂ V₁₃ W₂₃ c равными рёбрами и прямыми углами при вершине О₁₂₃ (рис. 9.37).

Изобразительной особеннос-

тью трёхкартинного комплексно-го чертежа такой плоскости яв-ляется взаимная перпендидику-лярность её следов (h°₁ ^ f°₂ ^ p°₃), из которых h°₁ || p°₃ || k₁₂₃, a f°₂ ^ k_{123 .}

На рис 9.37 способом засе-чек по трём известным сторо-нам построен треугольник следов в его натуральную величину, а способом прямоугольного треугольника определено значение угла j° наклона плоскости a к плоскостям проекций П₁, П₂ и П₃, а также расстояние Н от точки О₁₂₃ до плоскости a.

В о п р о с ы д л я п о в т о р е н и я:

1. Какова структура аппарата ортогональ-

ного проецирования?

2. Какая графическая конструкция на кар-

тине является определителем двухкартин-

ного комплекусного чертежа?

3. Какова структура аппарата получения

трёхкартинного комплексного чертежа?

4. Какова графическая структура опреде-

лителя трехкартинного комплексного чер-

тежа?

5. Каковы изобразительные свойства ор-

тогональных проекций точки на двухкар-

тинном комплексном чертеже?

6. Какая графическая конструкция обла-

дает свойствами графического алгоритма

преобразования двух любых проекций точ-ки в искомую третью?

7. Какова графическая структура 4-х, 5-ти

и 6-тикартинных чертежей точки?

8. Какие положения в пространстве может

занимать прямая линия?

9. Каковы позиционные и метрические

свойства ортогональных проекций линий

уровня?

10. Каковы позиционные и метрические

свойства ортогональных проекций проеци-

рующих прямых?

11. Как определить натуральную величину

отрезка прямой общего положения и углы

его наклона к плоскостям проекций?

12. Что такое след прямой линии и каково её основное изобразительное свойство?

13. Каковы графические признаки колли-

нейности точек на чертеже?

14. Как могут взаимно располагаться две

прямые в пространстве?

15. Каковы изобразительные свойства ор-

тогональных проекций двух параллельных

прямых;

16. Каковы изобразительные свойства ор-

тогональных проекций двух пересекающих-

ся прямых?

17. Каковы изобразительные свойства ор-

Тогональных проекций двух взаимно-пер-

пендикулярных прямы?

18. Каковы изобразительные свойства ор-

тогональных проекций двух скрещивающих-

ся прямых?

19. Какие точки двух скрещивающихся

прямых называются конкурирующими и как

с их помощью определять видимость эле-ментов на чертежах непрозрачных трёх-мерных объектов?

20. Какими элементами пространства мо-

гут быть заданы в нем плоскости?

21. Какие положения в пространстве мо-

жет занимать плоскость?

22. Какими позиционными и метрически-

ми свойствами обладают ортогональные проекции проецирующих плоскостей?

23. Какими позиционными и метрически-

ми свойствами обладают ортогональные проекции плоскостей уровня?

24. Что называется следами плоскости и

каковы их изобразительные свойства?

25. Каковы графические признаки компла-

нарности точек и линий?

26. В каких случаях прямой линейный угол проецируется на одну из плоскостей проекций в его натуральную величину?

27. Почему ортогональные проекции пло-

ской фигуры являются гомологичными фи-гурами?

28. Какие плоскости общего положения

являются равнонаклонёнными и каковы графические признаки их равнонаклонён-ности?

29. Какие плоскости общего положения

называются положительно равнонакло- нённми и каковы изобразительные свойст-

ва их ортогональных проекций?

30. Какие плоскости общего положения

называются отрицательно равнонаклонен-

клонёнными и какова изобразительные свойства их ортогональных проекций?

31. Какая плоскость общего положения

равнонаклонена к трём плоскостям проек-ций и каковы изобразительные свойства её ортогональных проекций?

Date: 2015-04-23; view: 558; Нарушение авторских прав