Дифференциальное уравнение теплопроводности. Распределение температуры в теле, описывается дифференциальным

Распределение температуры в теле, описывается дифференциальным

уравнением теплопроводности, которое при принятых допущениях, а именно: тело однородно и изотропно; физические параметры тела постоянны во времени и пространстве; температурные деформации рассматриваемого элементарного объема малы по сравнению с самим объемом; внутренние источники теплоты распределены в рассматриваемом объеме равномерно; макрочастицы тела неподвижны относительно друг друга; имеет следующий вид:

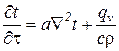
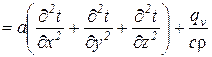, (13)

где – время, сек; 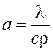– коэффициент температуропроводности, характеризующий скорость изменения температуры в любой точке тела, ;

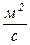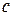– теплоемкость тела, 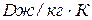; 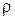– плотность тела, кг/м³; – объемная плотность тепловыделения, Bm/м³; 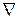– оператор Лапласа.

Уравнение (13) называется дифференциальным уравнением теплопроводности.

В цилиндрических координатах уравнение (13) имеет следующий вид:

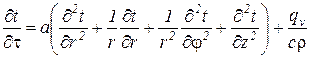, (14)

где 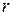– радиус вектор; 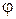– угол наклона радиуса–вектора.

Чтобы получить конкретное решение уравнения (13) для рассматриваемого случая, необходимо ввести полное математическое описание данного конкретного процесса теплопроводности. Эти частные особенности называются условиями однозначности или краевыми условиями, включающими:

· геометрические условия (форма, размеры тела);

· Физические условия (физические свойства тела и его физические параметры);

· Начальные условия (распределение температуры в теле в начальный момент времени);

· Граничные условия, определяющие взаимодействие тела с окружающей средой.

1. Граничные условия первого рода. Задается распределение температуры на поверхности тела, как функция координат и времени

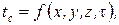(15)

где 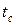-температура поверхности тела.

В частном случае, если температура поверхности тела постоянна выражение (15) имеет вид .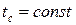

2. Граничные условия второго рода. Задается распределение плотности тепловогопотока на поверхности тела, как функция координат и времени

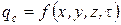. (16)

В частном случае, когда плотность теплового потока на поверхности тела остается постоянной, имеем .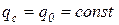

3. Граничные условия третьего рода. Задается температура окружающей среды 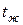и закон теплообмена между поверхностью тела и окружающей средой

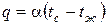если 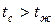, (17)

Уравнение (17) выражает закон Ньютона-Рихмана. Теплота, воспринятая поверхностью тела, распространяется в нем по закону Фурье. Следовательно, где 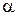– коэффициент теплообмена, представляющий собой плотность теплового потока подведенного (отведенного) к единице поверхности тела при разности температур между поверхностью тела и окружающей среды 1К, Вm/(м²К

на основании уравнений (16) и (17) имеем

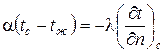. (18)

Индекс “ с” означает, что температурный градиент относится к поверхности тела.

Выражение (18) можно записать в виде

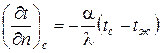. (19)

Уравнение (19) является аналитическим выражением граничных условий третьего рода.

4. Граничные условия четвертого рода. Отражают условия теплообмена системы тел имеющих различные значения коэффициентов теплопроводности. Между телами предполагается идеальный контакт. Тогда

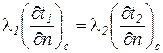, (20)

где 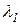– коэффициент теплопроводности первого тела; 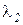– коэффициент те-плопроводности второго тела.

Date: 2015-05-09; view: 823; Нарушение авторских прав