Теорема Пригожина

Рассмотрим два сопряженных потока J₁ и J₂. Учитывая принцип симметрии, линейные уравнения можно представить в виде: J₁ = L₁₁F₁ + L₁₂F₂ та J₂ = L₂₁F₁ + L₂₂F₂, а выражение для продукции энтропии запишем как: dS/dt = L₁₁F₁² + (L₁₂ + L₂₁)F₁F₂ + L₂₂F₂².

Вычислим частные производные от продукции энтропии s = 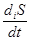по движущей силе F₁ (при постоянной F₂) и по движущей силе F₂ (при постоянной F₁):

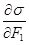= 2L₁₁F₁ + 2L₁₂F₂ = 2 J₁; (8.91)

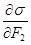= 2L₂₂F₂ + 2L₁₂F₁ = 2 J₂. (8.92)

Если в стационарном состоянии открытой системы J₁ = 0 и J₂ = 0, то 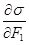= 0 и 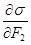= 0, то-есть скорость продукции энтропии приобретает максимальное значение. Из дифференциального исчисления известно, что если функция имеет максимум в определенной точке, то производная функции в этой точке может преобразовывать в ноль. Это необходимое, но недостаточное условие. Достаточным условием экстремума является поведение второй производной: если вторая производная в данной точке положительна, то функция в этой точке имеет минимум. В нашем случае величина s = 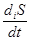всегда положительна для всей области изменений F₁ и F₂, первые производные 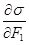и 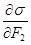равны нулю (необходимое условие минимума) и вторые производные 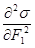и 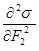также равны нулю (достаточное условие минимума); следовательно, продукция энтропии в стационарном состоянии принимает минимальные значения.

Принцип минимума продукции энтропии в стационарном состоянии открытой системы является важнейшим результатом линейной неравновесной термодинамики, поскольку предлагает количественный критерий установления стационарного состояния. Этот принцип сформулирован как теорема Пригожина - в стационарном состоянии, близком к термодинамическому равновесию, значения скорости продукции энтропии системы за счет необратимых процессов достигают отличного от нуля постоянного минимального значения:

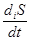® min, (8.93)

или

s ® min. (8.94)

Критерием приближения открытой системы к стационарному состоянию является отрицательность производной от продукции энтропии по времени:

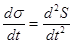< 0. (8.95)

Илья ПРИГОЖИН (1917-2003) Бельгийский физик (родился в Москве), известный определением понятия диссипативной структуры и ее роли в термодинамических системах вне состояния равновесия. Доказал теорему, названную его именем (1977 г.). Ряд работ посвященный математической роли детерминизма в нелинейных системах на классическом и квантовом уровнях. Лауреат Нобелевской премии по химии 1977 года.

КОНТРОЛЬНЫЕ ВОПРОСЫ И ЗАДАНИЯ

1. К какому типу термодинамических систем относятся живые организмы?

2. Что такое стационарное состояние?

3. За счет каких процессов происходит изменение энтропии в живых системах?

4. Пояснить, что такое негэнтропия.

5. Что называют продукцией энтропии? скоростью продукции энтропии?

6. Какие термодинамические процессы называются неравновесными?

7. Что такое диссипативная функция?

8. Сформулировать линейный закон термодинамики необратимых процессов.

9. Сформулировать и записать закон Фика.

10. Сформулировать и записать закон Гагена-Пуазейля

11. Сформулировать и записать закон Фурье.

12. Сформулировать и записать закон Ньютона.

13. Что такое конвекция?

14. От чего зависит граничный слой воздуха? Сформулировать теорему

Пригожина.