Закон качества, или структуры, вещества

Воспользуемся первой строчкой уравнений (15) и выразим, с учетом равенств (27) и (70), основные и перекрестные коэффициенты А в виде соответствующих функций f от экстенсоров Е. Имеем

А₁₁ = f₁₁(E₁; E₂)

А₁₂ = f₁₂(E₁; E₂) (72)

А₂₁ = f₂₁(E₁; E₂)

А₂₂ = f₂₂(E₁; E₂)

Для простоты мы ограничились только двумя степенями свобо­ды (n = 2); этого вполне достаточно, чтобы отразить все осо­бенности взаимного влияния различных явлений.

Не желая иметь дело с абсолютными значениями величин и неизвестными функциями f, мы, как и прежде, воспользуемся формальным математическим приемом дифференцирования функций нескольких переменных. Находим

dA₁₁ = B₁₁₁dE₁ + B₁₁₂dE₂

dA₁₂ = B₁₂₁dE₁ + B₁₂₂dE₂ (73)

dA₂₁ = B₂₁₁dE₁ + B₂₁₂dE₂

dA₂₂ = B₂₂₁dE₁ + B₂₂₂dE₂

где

В₁₁₁ = (¶А₁₁/¶E₁)_E2 = ¶²Р₁/¶E²₁ = ¶³U/¶E³₁;

В₁₁₂ = (¶А₁₁/¶E₂)_E1 = ¶²Р₁/(¶E₁¶E₂) = ¶³U/(¶E²₁¶E₂);

В₁₂₁ = (¶А₁₂/¶E₁)_E2 = ¶²Р₁/(¶E₂¶E₁) = ¶³U/(¶E²₁¶E₂);

В₁₂₂ = (¶А₁₂/¶E₂)_E1 = ¶²Р₁/(¶E²₂) = ¶³U/(¶E₁¶E²₂); (74)

В₂₁₁ = (¶А₂₁/¶E₁)_E2 = ¶²Р₂/(¶E²₁) = ¶³U/(¶E₂¶E²₁);

В₂₁₂ = (¶А₂₁/¶E₂)_E1 = ¶²Р₂/(¶E₁¶ E₂) = ¶³U/(¶E²₂¶E₁);

В₂₂₁ = (¶А₂₂/¶E₁)_E2 = ¶²Р₂/(¶E₂¶ E₁) = ¶³U/(¶E²₂¶E₁);

В₂₂₂ = (¶А₂₂/¶E₂)_E1 = ¶²Р₂/¶E²₂ = ¶³U/¶E³₂

В гипотетических условиях системы с одной степенью свободы (n = 1) имеем

А = f(E) (75)

dА = ВdE (76)

где В = dА/dE = d²Р/dE² = d³U/dE³ (77)

В формулах (74) и (77) производные от структур А определены через производные от интенсиалов Ρ с помощью равенств (55) и (56), а производные от интенсиалов - через производные от энергии с помощью равенств (37). Из формул (37), (55), (56) и (74) видно, какие экстенсоры при дифференцировании остаются постоянными.

Выведенные соотношения (73) и (76) представляют собой дифференциальные уравнения третьего порядка. Они опреде­ляют изменения структур А в зависимости от изменений экстенсоров Е.

В общем случае при n степенях свободы системы изменение любой данной структуры А складывается из n величин, каждая из которых пропорциональна изменению соответствующего экстенсора Ε; коэффициентами пропорциональности служат структуры В. Этот результат составляет содержание закона качества, или структуры, вещества.

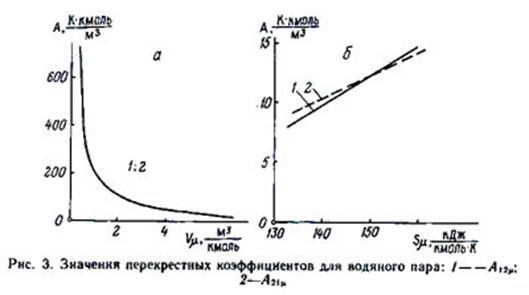Таким образом, мы определили специфические меры качества, или структуры, вещества А, играющие в уравнении состояния (54) роль коэффициентов пропорциональности. Конкретные зависимости величин А от экстенсоров (см. урав­нение (72)) можно наблюдать на примере рис. 3, а и б, где приведены мольные, отмеченные индексом μ, значения коэффициентов взаимности А_12m (сплошные линии 1) и А_21m (штриховые линии 2) в функции объема V_m (при S_m = 126 кДж/кмоль·К.) и энтропии S_m (при V_m = 18 м³/кмоль); коэффициенты найдены по известным справочным данным для водяного пара [17, с. 132]; соответствующие значения основных структур в функции тех же экстенсоров приведены в табл. 2 работы [17, с.126]. В рассматриваемом примере роль экстенсора для термических явлений играет энтропия S.

Из дальнейшего изложения станет ясно, что на процесс структурообразования системы решающее влияние оказывают интенсиалы, входящие в уравнение состояния (54) в виде разностей и производных первого порядка (см. соотношения (55) и (56)). Поэтому закон, позволяющий определять неиз­вестные коэффициенты структуры А уравнения состояния с помощью равенств (73) и (76), можно также назвать законом структуры первого порядка [ТРП, стр.120-122].

Date: 2015-05-09; view: 530; Нарушение авторских прав