Вывод уравнения

Приступим теперь к систематическому анализу основного уравнения ОТ для ансамбля простых явлений. Это позволит обнаружить у некоторых из введенных характеристик многие важные свойства, вывести дополнитель­ные уравнения и сформулировать новые законы. Такое углуб­ление содержания основных понятий теории будет осущест­вляться в ходе всего последующего изложения.

Обратим внимание на одну чрезвычайно важную особен­ность процесса переноса вещества через контрольную поверх­ность. При этом будет выявлено второе замечательное свойство природы, которое позволяет существенно расширить наши представления о веществе и его мере Е. Для количественного определения этого свойства выведем соответствующее диф­ференциальное уравнение.

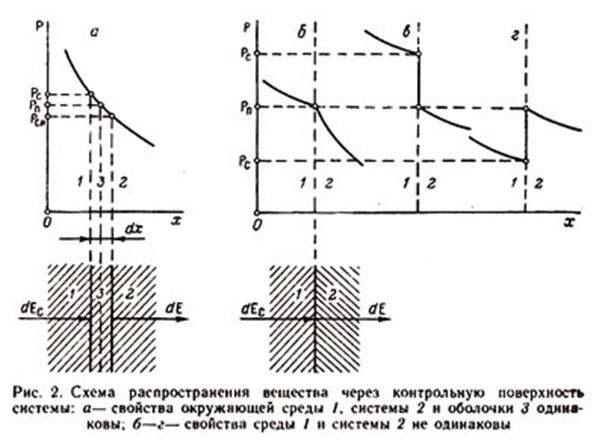
Предположим, что система 2 мысленно отделена от окру­жающей среды 1 оболочкой 3 толщиной dx (рис. 2, а). Свойства системы, оболочки и окружающей среды будем считать одина­ковыми. Следствием этой одинаковости, как мы убедимся в дальнейшем, является то, что кривая распределения данного интенсиала Ρ не претерпевает изломов или скачков на поверх­ностях соприкосновения оболочки с системой и окружающей средой. Предположим далее, что из окружающей среды в оболочку входит определенное количество вещества, мерой которого служит экстенсор dE_с. Одновременно из оболочки в систему выходит то же вещество в количестве dE. Опишем этот процесс с помощью первого начала, причем уравнение составим применительно к оболочке.

Для простоты будем считать, что система, оболочка и среда обладают одной сопряженной степенью свободы (n = 1). В этих условиях общее уравнение (31) первого начала приобретает вид

dU = P_cdE_c + P_сиdE, (47)

где Р_с - интенсиал поверхности окружающей среды; Р_си - интенсиал поверхности системы.

Если теперь толщину dx устремить к нулю, то оболочка превратится в обычную контрольную поверхность. При этом изменение энергии оболочки

dU = 0, (48)

так как геометрическая поверхность не способна накапливать или отдавать энергию, а интенсиалы Р_с и Р_си, станут равными интенсиалу Р_п контрольной поверхности, то есть

Р_с = Р_си = Р_п (49)

ибо величина Р_п является общей для системы и среды (рис. 2, а и б). С помощью соотношений (48) и (49) выражение (47) преобразуется к виду

dE + dE_c = 0 (50)

Это и есть искомое уравнение. Аналогичное равенство можно составить для любой сопряженной степени свободы системы и окружающей среды. Следовательно, уравнение (50) в общем случае справедливо для произвольного числа n [ТРП, стр.107-108].

Date: 2015-05-09; view: 540; Нарушение авторских прав