Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?
Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника
Статистическая физика
|
|
1. Задание {{ 40 }} Термодинамика-61
Коническое распределение Гиббса предполагает
R Систему в термостате.
2. Задание {{ 41 }} Термодинамика-62
Микроканоническое распределение предполагает
R Изолированную систему
3. Задание {{ 42 }} Термодинамика-63
Большое каноническое распределение предполагает
R Систему с переменным числом частиц.
4. Задание {{ 64 }} Термодинамика-64
Согласно классическому закону равнораспределения на одну степень свободы приходится энергия
R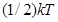 
5. Задание {{ 65 }} Термодинамика-65
Внутренняя энергия моля идеального газа равна
R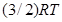 
6. Задание {{ 66 }} Термодинамика-66
Внутренняя энергия идеального газа
R Линейно растёт с ростом температуры
7. Задание {{ 67 }} Термодинамика-67
Теплоёмкость идеального газа
R Не зависит от температуры
8. Задание {{ 68 }} Термодинамика-68
Теплоёмкость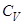 
одного моля идеального газа равна
R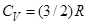 
9. Задание {{ 69 }} Термодинамика-69
Теплоёмкость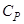 
одного моля идеального газа равна
R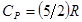 
10. Задание {{ 70 }} Термодинамика-70
Классическая теплоёмкость 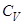одного моля двухатомного газа равна
R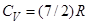 
11. Задание {{ 71 }} Термодинамика-71
Классическая теплоёмкость 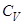одного моля твёрдого тела равна (закон Дюлонга и Пти)
R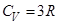 
12. Задание {{ 72 }} Термодинамика-72
Классическая теплоёмкость твёрдого тела равна (ниже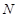 
- число атомов в теле)
R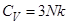 
13. Задание {{ 73 }} Термодинамика-73
Классическая теплоёмкость твёрдого тела
R Не зависит от температуры
14. Задание {{ 74 }} Термодинамика-74
Согласно классической статистике внутренняя энергия твёрдого тела
R Линейно растёт с ростом температуры
15. Задание {{ 75 }} Термодинамика-75
Согласно теории Дебая теплоёмкость твёрдого тела при стремлении температуры к нулю
R Стремится к нулю пропорционально кубу температуры
16. Задание {{ 76 }} Термодинамика-76
Поведение функции распределения в фазовом пространстве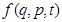 
описывается уравнением (уравнение Лиувилля), здесь 
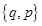соответствуют совокупности всех обобщённых координат и импульсов системы 
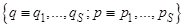, s - число степеней свободы.
R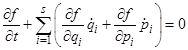 
17. Задание {{ 77 }} Термодинамика-77
Каноническое распределение Гиббса (здесь 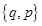- совокупность всех обобщённых координат и импульсов системы 
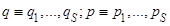, s - число степеней свободы)
R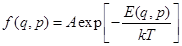 
, 
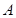-постоянная нормировки, 
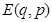- энергия системы
18. Задание {{ 78 }} Термодинамика-78
Микроканоническое распределение есть (выбрать правильные ответы), ниже 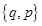- совокупность всех обобщённых координат и импульсов системы 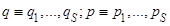, s - число степеней свободы
R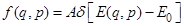 
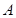, -постоянная нормировки, 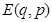- энергия системы
19. Задание {{ 79 }} Термодинамика-79
Величина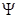 
в распределении 
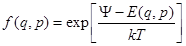имеет смысл (здесь 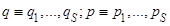, s - число степеней свободы)
R Свободная энергия системы
20. Задание {{ 80 }} Термодинамика-80
Энтропия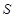 
выражается через функцию распределения 
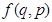по формуле (здесь , 
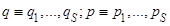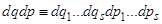, s - число степеней свободы)
R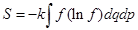 
21. Задание {{ 81 }} Термодинамика-81
Минимальный объём в фазовом пространстве, приходящийся на одну степень свободы равен
R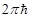 
22. Задание {{ 82 }} Термодинамика-82
Внутреннюю энергию системы в термостате можно вычислить по формуле (ниже 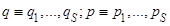, , 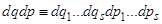s - число степеней свободы, 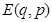- энергия системы)
R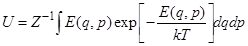 
, где 
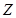- статистический интеграл
23. Задание {{ 83 }} Термодинамика-83
Статистический интеграл системы в термостате равен (ниже , ,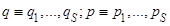 
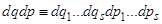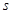- число степеней свободы, 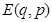- энергия системы)
R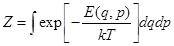 
24. Задание {{ 84 }} Термодинамика-84
Свободная энергия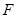 
связана со статистическим интегралом системы 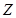соотношением (ниже 
)
R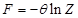 
25. Задание {{ 85 }} Термодинамика-85
Внутренняя энергия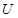 
связана со статистическим интегралом системы 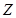соотношением (ниже )
R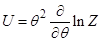 
26. Задание {{ 86 }} Термодинамика-86
Уравнение состояния системы выражается через статистический интеграл 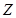уравнением (ниже )
R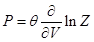 
27. Задание {{ 87 }} Термодинамика-87
Согласно классическому закону Релея-Джинса спектральная плотность энергии излучения абсолютно чёрного тела
R Пропорциональна температуре
28. Задание {{ 88 }} Термодинамика-88
Согласно квантовой формуле Планка спектральная плотность энергии излучения абсолютно чёрного тела
R Падает экспоненциально для больших частот
29. Задание {{ 89 }} Термодинамика-89
Квантовая формула Планка для спектральной плотности энергии излучения абсолютно чёрного тела
R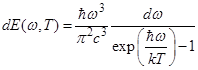 
30. Задание {{ 90 }} Термодинамика-90
Формула Вина для жёсткой части спектральной плотности энергии излучения абсолютно чёрного тела
R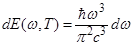 
31. Задание {{ 91 }} Термодинамика-91
Число квантовых состояний в единице объёма для фотонов с частотами в интервале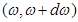 
есть (учесть наличие у фотона двух независимых поляризаций)
R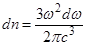 
32. Задание {{ 92 }} Термодинамика-92
Функция распределения равновесной системы имеет вид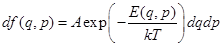 
, где 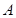- постоянная нормировки, 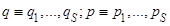, , 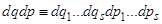s - число степеней свободы, 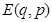- энергия системы. Указанное распределение справедливо для
R Для системы с постоянным числом частиц в термостате
33. Задание {{ 93 }} Термодинамика-93
Функция распределения равновесной системы имеет вид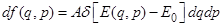 
, где 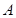- постоянная нормировки, 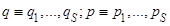, , 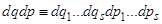s - число степеней свободы, 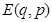- энергия системы. Указанное распределение справедливо для R Изолированной системы
34. Задание {{ 94 }} Термодинамика-94
Распределение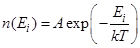 
где 
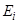- энергия i-го уровня, предполагает, что
R Частицы системы не взаимодействуют между собой и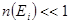 
35. Задание {{ 95 }} Термодинамика-95
Распределение 
предполагает, что (здесь 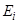- энергия i-го уровня, 
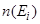-среднее число частиц в квантовом состоянии с энергией , )
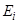R Имеется система бозонов и 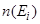произвольно
36. Задание {{ 96 }} Термодинамика-96
Распределение 
предполагает, что (здесь 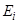- энергия i-го уровня, 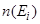-среднее число частиц в квантовом состоянии с энергией , )
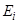R Частицы с полуцелым спином взаимодействуют между собой и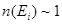 
37. Задание {{ 97 }} Термодинамика-97
Величина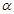 
в распределении 
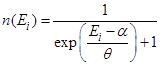есть (здесь 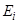- энергия i-го уровня, 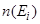-среднее число частиц в квантовом состоянии с энергией , )
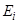R Химический потенциал
38. Задание {{ 98 }} Термодинамика-98
Величина 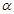в распределении 
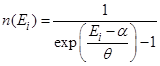есть (здесь 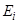- энергия i-го уровня, 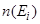-среднее число частиц в квантовом состоянии с энергией , )
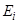R Химический потенциал
39. Задание {{ 99 }} Термодинамика-99
Распределение Ферми-Дирака имеет вид
R
40. Задание {{ 100 }} Термодинамика-100
Распределение Бозе-Эйнштейна имеет вид
R
41. Задание {{ 101 }} Термодинамика-101
Распределение Больцмана имеет вид
R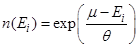 
42. Задание {{ 102 }} Термодинамика-102
Согласно распределению Максвелла равновесный идеальный газ распределён в конфигурационном пространстве
R Равномерно
43. Задание {{ 103 }} Термодинамика-103
Распределение Ферми-Дирака определяет
R Среднее число частиц с полуцелым спином в одном квантовом состоянии с заданной энергией
44. Задание {{ 104 }} Термодинамика-104
Распределение Бозе-Эйнштейна определяет
R Среднее число частиц с целым спином в одном квантовом состоянии с заданной энергией
45. Задание {{ 105 }} Термодинамика-105
Вывести условие, при котором распределения Ферми-Дирака, Бозе-Эйнштейна и Больцмана совпадают (ниже , 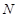- число частиц в системе с объёмом 
)
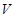R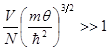 
46. Задание {{ 106 }} Термодинамика-106
Выражение 
определяет (здесь , 
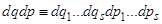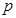и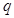 
- обобщённые координаты и импульсы системы с числом степеней s)
R Число квантовых состояний в заданном элементе фазового объёма
47. Задание {{ 107 }} Термодинамика-107
Пусть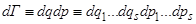 
и 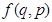- равновесная функция распределения. Тогда внутренняя энергия системы может быть вычислена по формуле
R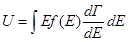 
, где 
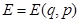- энергия системы
48. Задание {{ 108 }} Термодинамика-108
Уравнение состояния вырожденного электронного газа
R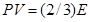 
, где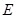 
- энергия газа
49. Задание {{ 109 }} Термодинамика-109
Температура вырождения электронного газа R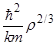 
, где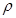 
- плотность
50. Задание {{ 110 }} Термодинамика-110
С квантовомеханической точки зрения при сообщении тепла системе
R Меняется населённость уровней энергии при неизменном их расположении
51. Задание {{ 111 }} Термодинамика-111
С квантовомеханической точки зрения при совершении работы макроскопической системой в адиабатическом процессе
R Уровни энергии системы сдвигаются при неизменной их населённости
52. Задание {{ 112 }} Термодинамика-112
Каноническое распределение Гиббса для системы из 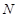тождественных частиц в квазиклассическом случае может быть записано в виде (ниже 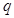и 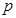- совокупность координат импульсов частиц системы, 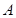-постоянная нормировки, 
)
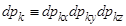R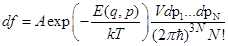 
53. Задание {{ 113 }} Термодинамика-113
Вычислить квазиклассическую статистическую сумму идеального газа
R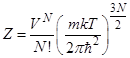 
54. Задание {{ 114 }} Термодинамика-114
Распределение частиц одноатомного идеального газа в термостате по энергиям имеет вид (везде А - константа нормировки)
R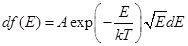 
55. Задание {{ 115 }} Термодинамика-115
Распределение частиц одноатомного идеального газа в термостате по энергиям имеет вид (везде )
R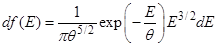 
56. Задание {{ 116 }} Термодинамика-116
Большое каноническое распределение для систем с переменным числом частиц в классической статистике имеет вид (ниже ;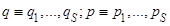 
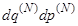- элемент фазового объёма для 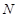частиц, 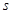- число соответствующих степеней свободы, 
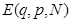- энергия системы, число частиц в которой , 
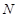- большой термодинамический потенциал, 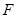- свободная энергия)
R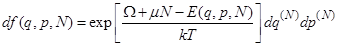 
57. Задание {{ 117 }} Термодинамика-117
Пусть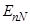 
- уровни энергии системы, число частиц 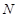в которой меняется, тогда большой термодинамический потенциал определяется выражением
R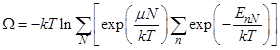 
58. Задание {{ 118 }} Термодинамика-118
Матрица плотности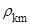 
удовлетворяет соотношениям (выбрать правильные ответы)
R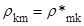 
R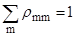 
R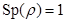 
59. Задание {{ 119 }} Термодинамика-119
Среднее значение физической величины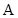 
определяется по матрице плотности 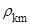как (
- оператор) (выбрать правильные ответы)
R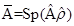 
R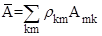 
60. Задание {{ 120 }} Термодинамика-120
Статистический оператор системы в произвольном представлении определяется как
R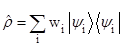 
, где 
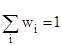и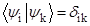 
61. Задание {{ 191 }} Термодинамика-191
Микроканоническое распределение для системы одномерных гармонических осцилляторов
R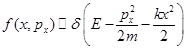 
62. Задание {{ 192 }} Термодинамика-192
Каноническое распределение Гиббса для системы одномерных гармонических осцилляторов
R 
63. Задание {{ 194 }} Термодинамика-194
Излучаемая в равновесных условиях абсолютно чёрным телом энергия пропорциональна
R Четвёртой степени температуры
64. Задание {{ 195 }} Термодинамика-195
Уравнение состояния неидеального газа
R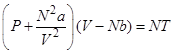 
65. Задание {{ 197 }} Термодинамика-197
Закон Стефана-Больцмана
R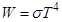 
66. Задание {{ 198 }} Термодинамика-198
В условиях статистического равновесия
R Частицы распределены равномерно на поверхности с постоянной энергией.
67. Задание {{ 200 }} Термодинамика-200
Химический потенциал газа фотонов
R Равен нулю
Уникальный идентификатор НТЗ: ID = 687673279
Наименование НТЗ: Термодинамика и статфизика
Расположение НТЗ: \\172.16.24.4\test\физический факультет\кафедра теоретической физики\термодинамика и статфизика_ok.ast
Авторский коллектив НТЗ: Хоконов Мурат Хазреталиевич
Дата создания НТЗ: 01.11.2003
Дата конвертации НТЗ: 25.02.2008
ВЫБОРОЧНОЕ СОДЕРЖАНИЕ ТЕСТОВЫХ МАТЕРИАЛОВ
Date: 2015-05-09; view: 1369; Нарушение авторских прав