Уравнения состояния

При выводе основных уравнений состояния в термодинамике в качестве рабочего тела рассматривается идеальный газ. Под идеальным условно понимается газ, у которого отсутствуют силы взаимодействия между молекулами, а сами молекулы рассматриваются как лишенные объема, хотя они являются материальными частицами. Понятие “идеальный газ” упрощает термодинамические исследования и обеспечивает при низких давлениях и высоких температурах приемлемую точность результатов.

Рассматриваемые ниже закономерности справедливы для идеальных газов.

Для 1 кг идеального газа уравнение состояния имеет вид

,

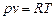где р - давление, Па; v - удельный объем, м³/кг; Т - абсолютная температура, К; R - удельная газовая постоянная, Дж/кг×К.

Для m кг газа, если учесть, что 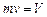, уравнение состояния идеального газа получает вид

,

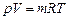где V - объем m кг газа, м³.

Для 1 кмоля уравнение состояния имеет вид

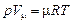
где V_m - объем 1 кмоля газа, м³/кмоль; 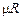- универсальная газовая постоянная, численно равная работе, совершаемой 1 кмолем идеального газа при нагревании на один градус, Дж/кмоль×К.

Уравнение состояния идеального газа, записанное для разных количеств в трех видах называется также характеристическим уравнением Клапейрона - Менделеева, как полученное вначале для 1 кг Клапейроном, а затем обобщенное Менделеевым. Исторически физические законы Бойля-Мариотта и Гей-Люссака появились раньше, чем уравнение состояния, однако их можно рассматривать как его частные случаи. Действительно, если Т = cons t, то из первого уравнения состояния получаем

или .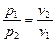

Эти уравнения выражают собой закон Бойля-Мариотта. Если 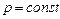, то для двух состояний газа можем записать,

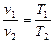- Закон Гей-Люссака.

Удельная газовая постоянная R для каждого газа при любых условиях сохраняет свое определенное значение. Для определения газовой постоянной воспользуемся тем, что объемы 1 кмоля идеальных газов при одинаковых температурах и давлении приблизительно одинаковы. При нормальных условиях 1 кмоль всех идеальных газов равен 22,414 м³/кмоль. Приняв нормальные условия и подставив значения параметров для них в выражение для R, найдем

Дж/кмоль×К,

т.е. универсальная газовая постоянная одинакова для всех газов. Так как 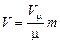, то подставив значение молярного объема V_m в основное уравнение состояния идеального газа, получим

,

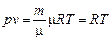где 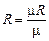- удельная газовая постоянная, Дж/кг×К.

Удельная газовая постоянная численно равна работе, которую совершает 1 кг идеального газа при нагревании его на один градус. Между универсальной газовой постоянной R и удельной газовой постоянной существует связь

Дж/кмоль×К. кг/м³,

а удельный объем 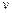по обратной формуле

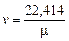м³/кг,

где V_m = 22,414 м³/кмоль - объем 1 кмоля идеального газа.

С помощью уравнения состояния можно решать задачи по определению массы некоторого количества газа или какого-либо его параметра, если заданы остальные.

Пример 1.1. Определить массу кислорода, содержащегося в баллоне вместимостью V = 0,08 м³ при t = 27°С и р = 2,5 МПа.

Р е ш е н и е. Определим удельную газовую постоянную для газа кислорода

Дж/кг×град.

Определим абсолютную температуру

Т = t + 273 = 27 + 273 = 300°К.

Из уравнения состояния находим

кг.

Пример 1.2. Паротурбинная установка мощностью 500000 кВт расходует 335 г условного топлива на 1 кВт×ч. Определить массу воздуха, которую необходимо подать в топку котла за 1 ч, если для сжигания 1 кг топлива требуется 16 м³ воздуха при давлении 750 мм рт. ст. (100 кПа), приведенном к 0°С и температуре 15°С.

Р е ш е н и е. За 1 час работы котла требуется топлива:

500000´0,335 = 167500 кг.

На каждый 1 кг топлива необходимо подать в топку котла 16 м³ воздуха, или за 1 час работы требуется воздуха:

167500´16 = 2680000 м³.

Масса этого объема воздуха составит

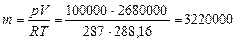кг = 3220 т/ч.

Date: 2015-05-09; view: 1283; Нарушение авторских прав