Главная
Случайная страница
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?
Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника
|
Электричество и магнетизм 1 Электростатическое поле в вакууме
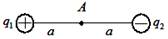 Электрическое поле создано двумя точечными зарядами q 1=+ q, q 2=- q. Напряжённость и потенциал в точке А равны … Электрическое поле создано двумя точечными зарядами q 1=+ q, q 2=- q. Напряжённость и потенциал в точке А равны …
| 1: 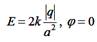 *
2: *
2: 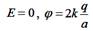 3:
3: 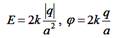 4:
4: 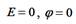
| 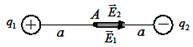 Согласно принципу суперпозиции Согласно принципу суперпозиции 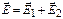 , φ = φ 1+ φ 2 (алгебраическая сумма). Векторы , φ = φ 1+ φ 2 (алгебраическая сумма). Векторы 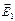 и и 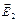 показаны на рисунке. Учитывая, что показаны на рисунке. Учитывая, что 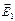 и и 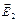 направлены в одну сторону, направлены в одну сторону, 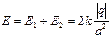 . . 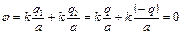 . Ответ: 1 . Ответ: 1
|
Протон и электрон ускоряются электростатическим полем, пройдя одинаковую разность потенциалов. При этом отношение скоростей 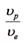 будет равно … будет равно …
| 1: 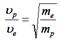 * 2: * 2: 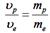 3:
3: 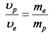 4: 4: 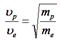
| Работа сил электростатического поля приведёт к увеличению кинетической энергии: 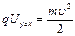 . Отсюда скорость частицы будет равна . Отсюда скорость частицы будет равна 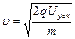 . Следовательно, отношение скоростей протона и электрона . Следовательно, отношение скоростей протона и электрона  . Ответ: 1 . Ответ: 1
|
 На рисунке изображены силовые линии электростатического поля. Укажите верное соотношение для величины напряжённости Е поля в точках А, В и С. На рисунке изображены силовые линии электростатического поля. Укажите верное соотношение для величины напряжённости Е поля в точках А, В и С.
| 1: EA > EB > EC*
2: EA < EB < EC
3: EA = EC < EB
4: EA > EB = EC
| | По густоте линий напряжённости можно судить о величине напряжённости поля: там, где линии гуще, величина напряжённости поля больше. Поэтому EA > EB > EC. Ответ: 1
|
| Работа сил электростатического поля при перемещении заряда -2 мкКл из точки поля с потенциалом 20 В в точку с потенциалом 40 В равна …
| 1: 40·10-6 Дж *
2: - 40·10-6 Дж
3: 40· Дж
4: - 40· Дж
| | Работа сил поля по перемещению заряда q в электростатическом поле вычисляется по формуле A = q (φ 1 – φ 2), φ 1 и φ 2 – потенциалы начальной и конечной точек поля. A = q (φ 1 – φ 2)=(– 2·10-6)(20 – 40) Дж = 40·10-6 Дж. Ответ: 1
|
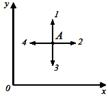 В некоторой области пространства создано электростатическое поле, потенциал которого описывается функцией. Вектор напряжённости электрического поля в точке А будет иметь направление, показанное стрелкой … В некоторой области пространства создано электростатическое поле, потенциал которого описывается функцией. Вектор напряжённости электрического поля в точке А будет иметь направление, показанное стрелкой …
| 1: 3*
2: 1
3: 4
4: 2
| Связь напряжённости и потенциала электростатического поля имеет вид:, 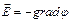 или в проекциях на оси прямоугольной декартовой системы координат: или в проекциях на оси прямоугольной декартовой системы координат: 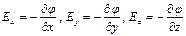 . Так как по условию потенциал φ зависит только от y, отлична от нуля только и . Так как по условию потенциал φ зависит только от y, отлична от нуля только и 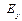 и и 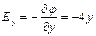 . Таким образом, вектор напряжённости электрического поля в точке А будет иметь направление, показанное стрелкой 3.. Ответ: 1 . Таким образом, вектор напряжённости электрического поля в точке А будет иметь направление, показанное стрелкой 3.. Ответ: 1
|
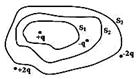 Дана система точечных зарядов в вакууме и замкнутые поверхности S1, S2 и S3, причём поверхность S3 охватывает поверхность S2, которая в свою очередь охватывает поверхность S1 (рис.). Поток напряжённости электростатического поля отличен от нуля сквозь … Дана система точечных зарядов в вакууме и замкнутые поверхности S1, S2 и S3, причём поверхность S3 охватывает поверхность S2, которая в свою очередь охватывает поверхность S1 (рис.). Поток напряжённости электростатического поля отличен от нуля сквозь …
| 1: поверхность S3
2: поверхности S2 и S3
3: поверхность S2
4: поверхность S1*
| Согласно теореме Остроградского-Гаусса, поток вектора напряжённости электростатического поля в вакууме сквозь произвольную замкнутую поверхность равен отношению алгебраической суммы электрических зарядов, охватываемых этой поверхностью, и электрической постоянной ε 0, т.е. 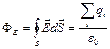 . Из условия видим, что . Из условия видим, что 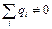 только для поверхности S1, поэтому поток вектора напряжённости электростатического поля отличен от нуля сквозь поверхность S1. Ответ: 4 только для поверхности S1, поэтому поток вектора напряжённости электростатического поля отличен от нуля сквозь поверхность S1. Ответ: 4
|
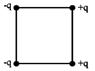 Каждый из четырёх одинаковых по модулю точечных зарядов (см. рис.), расположенных в вершинах квадрата, создаёт в точке пересечения диагоналей электрическое поле, напряжённость которого равна. Градиент потенциала поля в это точке равен ____ и направлен горизонтально … Каждый из четырёх одинаковых по модулю точечных зарядов (см. рис.), расположенных в вершинах квадрата, создаёт в точке пересечения диагоналей электрическое поле, напряжённость которого равна. Градиент потенциала поля в это точке равен ____ и направлен горизонтально …
| 1: 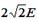 , вправо*
2: , вправо*
2: 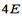 , влево
3: , влево
3: 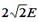 , влево
4: , влево
4: 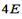 , вправо , вправо
| 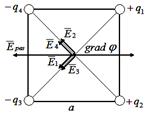 Градиент потенциала в некоторой точке связан с напряжённостью электрического поля в этой точке соотношением: Градиент потенциала в некоторой точке связан с напряжённостью электрического поля в этой точке соотношением: 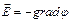 . Поэтому для нахождения grad φ в точке пересечения диагоналей квадрата необходимо найти напряжённость электрического поля в этой точке. Согласно принципу суперпозиции полей, напряжённость в точке пересечения диагоналей квадрата равна: . Поэтому для нахождения grad φ в точке пересечения диагоналей квадрата необходимо найти напряжённость электрического поля в этой точке. Согласно принципу суперпозиции полей, напряжённость в точке пересечения диагоналей квадрата равна: 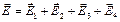 , где , где 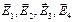 – напряжённости полей, создаваемых точечными зарядами + q 1, + q 2, - q 3, - q 4 в рассматриваемой точке соответственно. На рисунке показаны направления этих векторов. Величина напряжённости поля точечного заряда определяется по формуле – напряжённости полей, создаваемых точечными зарядами + q 1, + q 2, - q 3, - q 4 в рассматриваемой точке соответственно. На рисунке показаны направления этих векторов. Величина напряжённости поля точечного заряда определяется по формуле 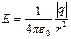 , где ε 0 – электрическая постоянная, а r – расстояние от заряда до точки. Поскольку все заряды одинаковы по величине и рассматриваемая точка одинаково удалена от каждого заряда, модули векторов , где ε 0 – электрическая постоянная, а r – расстояние от заряда до точки. Поскольку все заряды одинаковы по величине и рассматриваемая точка одинаково удалена от каждого заряда, модули векторов 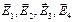 равны, т.е. Е 1= Е 2= Е 3= Е 4= Е, а равны, т.е. Е 1= Е 2= Е 3= Е 4= Е, а 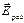 образует диагональ квадрата со стороной 2 Е. Модуль напряжённости результирующего электрического поля в центре квадрата образует диагональ квадрата со стороной 2 Е. Модуль напряжённости результирующего электрического поля в центре квадрата 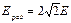 . Учитывая связь напряжённости электрического поля и потенциала, градиент потенциала в центре квадрата равен . Учитывая связь напряжённости электрического поля и потенциала, градиент потенциала в центре квадрата равен 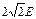 и направлен вправо. Ответ: 1 и направлен вправо. Ответ: 1
|
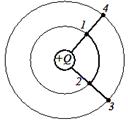 Установите соответствие между величиной (знаком) работы сил электростатического поля, создаваемого зарядом + Q, по перемещению отрицательного заряда - q и траекторией перемещения (указаны начальная и конечная точки).
1. А =0 А. 1-2
2. А <0 Б. 2-3
В. 3-1 Установите соответствие между величиной (знаком) работы сил электростатического поля, создаваемого зарядом + Q, по перемещению отрицательного заряда - q и траекторией перемещения (указаны начальная и конечная точки).
1. А =0 А. 1-2
2. А <0 Б. 2-3
В. 3-1
| 1: 1-А, 2-Б*
2: 1-В, 2-А
3: 1-В, 2-Б
| Работа сил электростатического поля по перемещению заряда q из точки 1 в точку 2 определяется по формуле: A 12= q (φ 1 – φ 2). Отсюда следует, что A 12=0, если φ 1= φ 2. Точки, имеющие одинаковый потенциал, лежат на одинаковом расстоянии от заряда, создающего поле 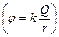 , поэтому А =0 для траектории 1-2. А 23= q (φ 2 – φ 3) < 0 для траектории 2-3, поскольку φ 2> φ 3, а q < 0. А 31= q (φ 3 – φ 1) > 0 для траектории 2-3, поскольку φ 2< φ 3, а q < 0. Ответ: 1 , поэтому А =0 для траектории 1-2. А 23= q (φ 2 – φ 3) < 0 для траектории 2-3, поскольку φ 2> φ 3, а q < 0. А 31= q (φ 3 – φ 1) > 0 для траектории 2-3, поскольку φ 2< φ 3, а q < 0. Ответ: 1
|
Установите соответствие между источником электростатического поля и формулой, позволяющей вычислить напряжённость поля в некоторой точке.
1. Точечный заряд А. 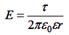 2. Равномерно заряженная длинная нить Б.
2. Равномерно заряженная длинная нить Б. 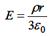 3. Равномерно заряженная бесконечная плоскость В.
3. Равномерно заряженная бесконечная плоскость В.  Г.
Г. 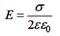
| 1: 1-В, 2-А, 3-Г*
2: 1-А, 2-Б, 3-В
3: 1-В, 2-Б, 3-Г
4: 1-Б, 2-А, 3-Г
| | Напряжённость поля точечного заряда в некоторой точке обратно пропорциональна квадрату расстояния до заряда; напряжённость поля равномерно заряженной длинной нити обратно пропорциональная расстоянию до нити; напряжённость поля равномерно заряженной бесконечной плоскости на зависит от расстояния до плоскости. Ответ: 1
|
Date: 2015-05-09; view: 12865; Нарушение авторских прав | Понравилась страница? Лайкни для друзей: |
|
|



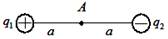 Электрическое поле создано двумя точечными зарядами q 1=+ q, q 2=- q. Напряжённость и потенциал в точке А равны …
Электрическое поле создано двумя точечными зарядами q 1=+ q, q 2=- q. Напряжённость и потенциал в точке А равны …
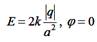 *
2:
*
2: 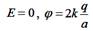 3:
3: 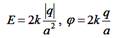 4:
4: 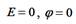
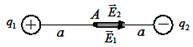 Согласно принципу суперпозиции
Согласно принципу суперпозиции 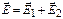 , φ = φ 1+ φ 2 (алгебраическая сумма). Векторы
, φ = φ 1+ φ 2 (алгебраическая сумма). Векторы 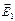 и
и 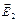 показаны на рисунке. Учитывая, что
показаны на рисунке. Учитывая, что 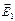 и
и 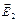 направлены в одну сторону,
направлены в одну сторону, 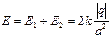 .
. 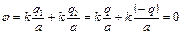 . Ответ: 1
. Ответ: 1
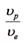 будет равно …
будет равно …
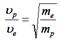 * 2:
* 2: 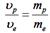 3:
3: 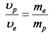 4:
4: 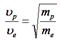
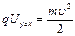 . Отсюда скорость частицы будет равна
. Отсюда скорость частицы будет равна 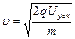 . Следовательно, отношение скоростей протона и электрона
. Следовательно, отношение скоростей протона и электрона  . Ответ: 1
. Ответ: 1
 На рисунке изображены силовые линии электростатического поля. Укажите верное соотношение для величины напряжённости Е поля в точках А, В и С.
На рисунке изображены силовые линии электростатического поля. Укажите верное соотношение для величины напряжённости Е поля в точках А, В и С.
 В некоторой области пространства создано электростатическое поле, потенциал которого описывается функцией. Вектор напряжённости электрического поля в точке А будет иметь направление, показанное стрелкой …
В некоторой области пространства создано электростатическое поле, потенциал которого описывается функцией. Вектор напряжённости электрического поля в точке А будет иметь направление, показанное стрелкой …
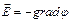 или в проекциях на оси прямоугольной декартовой системы координат:
или в проекциях на оси прямоугольной декартовой системы координат: 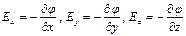 . Так как по условию потенциал φ зависит только от y, отлична от нуля только и
. Так как по условию потенциал φ зависит только от y, отлична от нуля только и 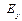 и
и 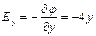 . Таким образом, вектор напряжённости электрического поля в точке А будет иметь направление, показанное стрелкой 3.. Ответ: 1
. Таким образом, вектор напряжённости электрического поля в точке А будет иметь направление, показанное стрелкой 3.. Ответ: 1
 Дана система точечных зарядов в вакууме и замкнутые поверхности S1, S2 и S3, причём поверхность S3 охватывает поверхность S2, которая в свою очередь охватывает поверхность S1 (рис.). Поток напряжённости электростатического поля отличен от нуля сквозь …
Дана система точечных зарядов в вакууме и замкнутые поверхности S1, S2 и S3, причём поверхность S3 охватывает поверхность S2, которая в свою очередь охватывает поверхность S1 (рис.). Поток напряжённости электростатического поля отличен от нуля сквозь …
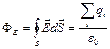 . Из условия видим, что
. Из условия видим, что 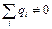 только для поверхности S1, поэтому поток вектора напряжённости электростатического поля отличен от нуля сквозь поверхность S1. Ответ: 4
только для поверхности S1, поэтому поток вектора напряжённости электростатического поля отличен от нуля сквозь поверхность S1. Ответ: 4
 Каждый из четырёх одинаковых по модулю точечных зарядов (см. рис.), расположенных в вершинах квадрата, создаёт в точке пересечения диагоналей электрическое поле, напряжённость которого равна. Градиент потенциала поля в это точке равен ____ и направлен горизонтально …
Каждый из четырёх одинаковых по модулю точечных зарядов (см. рис.), расположенных в вершинах квадрата, создаёт в точке пересечения диагоналей электрическое поле, напряжённость которого равна. Градиент потенциала поля в это точке равен ____ и направлен горизонтально …
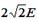 , вправо*
2:
, вправо*
2: 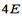 , влево
3:
, влево
3: 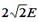 , влево
4:
, влево
4: 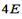 , вправо
, вправо
 Градиент потенциала в некоторой точке связан с напряжённостью электрического поля в этой точке соотношением:
Градиент потенциала в некоторой точке связан с напряжённостью электрического поля в этой точке соотношением: 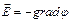 . Поэтому для нахождения grad φ в точке пересечения диагоналей квадрата необходимо найти напряжённость электрического поля в этой точке. Согласно принципу суперпозиции полей, напряжённость в точке пересечения диагоналей квадрата равна:
. Поэтому для нахождения grad φ в точке пересечения диагоналей квадрата необходимо найти напряжённость электрического поля в этой точке. Согласно принципу суперпозиции полей, напряжённость в точке пересечения диагоналей квадрата равна: 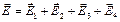 , где
, где 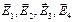 – напряжённости полей, создаваемых точечными зарядами + q 1, + q 2, - q 3, - q 4 в рассматриваемой точке соответственно. На рисунке показаны направления этих векторов. Величина напряжённости поля точечного заряда определяется по формуле
– напряжённости полей, создаваемых точечными зарядами + q 1, + q 2, - q 3, - q 4 в рассматриваемой точке соответственно. На рисунке показаны направления этих векторов. Величина напряжённости поля точечного заряда определяется по формуле 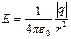 , где ε 0 – электрическая постоянная, а r – расстояние от заряда до точки. Поскольку все заряды одинаковы по величине и рассматриваемая точка одинаково удалена от каждого заряда, модули векторов
, где ε 0 – электрическая постоянная, а r – расстояние от заряда до точки. Поскольку все заряды одинаковы по величине и рассматриваемая точка одинаково удалена от каждого заряда, модули векторов 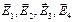 равны, т.е. Е 1= Е 2= Е 3= Е 4= Е, а
равны, т.е. Е 1= Е 2= Е 3= Е 4= Е, а 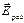 образует диагональ квадрата со стороной 2 Е. Модуль напряжённости результирующего электрического поля в центре квадрата
образует диагональ квадрата со стороной 2 Е. Модуль напряжённости результирующего электрического поля в центре квадрата 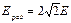 . Учитывая связь напряжённости электрического поля и потенциала, градиент потенциала в центре квадрата равен
. Учитывая связь напряжённости электрического поля и потенциала, градиент потенциала в центре квадрата равен 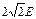 и направлен вправо. Ответ: 1
и направлен вправо. Ответ: 1
 Установите соответствие между величиной (знаком) работы сил электростатического поля, создаваемого зарядом + Q, по перемещению отрицательного заряда - q и траекторией перемещения (указаны начальная и конечная точки).
1. А =0 А. 1-2
2. А <0 Б. 2-3
В. 3-1
Установите соответствие между величиной (знаком) работы сил электростатического поля, создаваемого зарядом + Q, по перемещению отрицательного заряда - q и траекторией перемещения (указаны начальная и конечная точки).
1. А =0 А. 1-2
2. А <0 Б. 2-3
В. 3-1
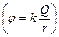 , поэтому А =0 для траектории 1-2. А 23= q (φ 2 – φ 3) < 0 для траектории 2-3, поскольку φ 2> φ 3, а q < 0. А 31= q (φ 3 – φ 1) > 0 для траектории 2-3, поскольку φ 2< φ 3, а q < 0. Ответ: 1
, поэтому А =0 для траектории 1-2. А 23= q (φ 2 – φ 3) < 0 для траектории 2-3, поскольку φ 2> φ 3, а q < 0. А 31= q (φ 3 – φ 1) > 0 для траектории 2-3, поскольку φ 2< φ 3, а q < 0. Ответ: 1
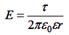 2. Равномерно заряженная длинная нить Б.
2. Равномерно заряженная длинная нить Б. 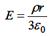 3. Равномерно заряженная бесконечная плоскость В.
3. Равномерно заряженная бесконечная плоскость В.  Г.
Г.