Дифференциальное уравнение электромагнитной волны. Одним из важнейших следствий уравнений Максвелла является существование электромагнитных волн

Одним из важнейших следствий уравнений Максвелла является существование электромагнитных волн. Из уравнений Максвелла следует, что векторы напряженностей В и Н переменного электромагнитного поля удовлетворяют волновому уравнению типа

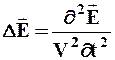, (2.1)

где D=¶²/¶x²+¶²/¶y²+¶²/¶z² - оператор Лапласа, V - фазовая скорость.

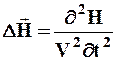(2.2)

Всякая функция, удовлетворяющая уравнениям (2.1.) и (2.2.), описывает некоторую волну. Следовательно, электромагнитные поля действительно могут существовать в виде электромагнитных волн. Фазовая скорость электромагнитных волн определяется выражением

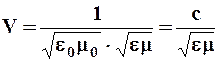, (2.3)

где 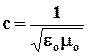; e₀ и m₀ - соответственно электрическая и магнитная постоянные; e и m - соответственно электрическая и магнитная проницаемости среды. В вакууме (при e=1 и m=1) скорость распространения электромагнитных волн совпадает со скоростью с. Так как em>1, то скорость распространения электромагнитных волн в веществе всегда меньше, чем в вакууме.

При вычислении скорости распространения электромагнитного поля по формуле (2.3) получается результат, достаточно хорошо совпадающий с экспериментальными данными, если учитывать зависимость e и m от частоты. Совпадение же размерного коэффициента в (2.3) со скоростью распространения света в вакууме указывает на глубокую связь между электромагнитными явлениями, позволившую Максвеллу создать электромагнитную теорию света, согласно которой свет представляет собой электромагнитные волны.

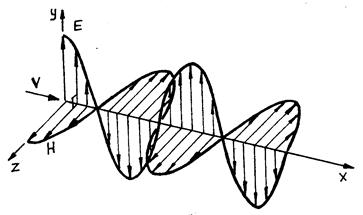
Рис. 6

Следствием теории Максвелла является поперечность электромагнитных волн: векторы Е и Н напряженностей электрического и магнитного полей волны взаимно перпендикулярны (на рис.6 показана моментальная <<фотография>> плоской электромагнитной волны) и лежат в плоскости, перпендикулярной вектору v скорости распространения

волны, причем векторы Е, Н и v образуют правовинтовую систему. Из уравнений Максвелла следует также, что в электромагнитной волне векторы Е и Н всегда колеблются в одинаковых фазах (см. рис.6), причем мгновенные значения Е и Н в любой точке связаны соотношением

. (2.4)

Следовательно, Е и Н одновременно достигают максимума, одновременно обращаются в нуль и т.д.

Date: 2015-05-08; view: 601; Нарушение авторских прав