Введение. Эффект Холла – возникновение поперечной разности потенциалов (между боковыми обкладками пластины перпендикулярно направлению магнитного поля и плотности тока)

Эффект Холла – возникновение поперечной разности потенциалов (между боковыми обкладками пластины перпендикулярно направлению магнитного поля и плотности тока) в пластине по которой течёт электрический ток при помещении её в магнитное поле направленному перпендикулярно плотности тока (магнитное поле имеет ненулевую составляющую в направлении перпендикулярном плотности тока).

Возникновение поперечной разности потенциалов обусловлено действием на упорядоченно движущийся заряд силы Лоренца со стороны магнитного поля. Схема возникновения эффекта Холла для положительных носителей тока и отрицательных носителей тока приведены на рис. 1, а и рис. 1, б соответственно.

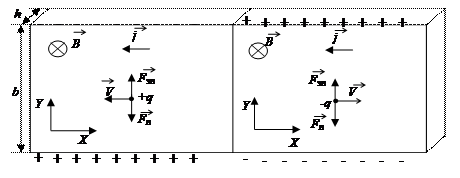а б

Рис. 1

Если пластина изготовлена из металла, то носителем тока является электрон – отрицательно заряженная частица. В этом случае схема возникновения эффекта Холла соответствует рис. 1, б. Для этого случая, в равновесном состоянии, сила Лоренца компенсируется электрической силой возникающей за счёт индуцированных зарядов.

Тогда предполагая, что поле индуцированных зарядов однородно получим:

,

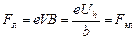где e – заряд электрона; V – средняя упорядоченная скорость носителя; B – вектор магнитной индукции; b – высота пластины; U_h – холловская разность потенциалов.

С учётом того, что вдоль оси Y ток не идёт, скорость по этой оси равна нулю и скорость определяется только током, текущим вдоль оси X. Тогда 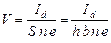, где S – площадь поперечного сечения пластины; h – толщина пластины; n – концентрация носителей тока; I_d – сила тока в пластине (ток датчика). Таким образом, для холловской разности потенциалов получим:

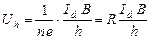, (1)

где R является константой для данного вещества и называется постоянной Холла. Она определяется выражением:

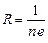. (2)

В этом случае подвижность носителей тока определяется как

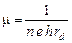, (3)

где r_d – сопротивление датчика Холла (r_d = 2,0 Ом).

В случае, если носителем тока является положительный заряд величина холловской разности потенциалов определяется выражением (1), как и для отрицательного заряда, однако, как видим из рис. 1, a, знак этой разности потенциалов противоположен знаку для отрицательного заряда.

В полупроводниках имеются как положительные заряды (дырки), так и отрицательные (электроны). Для случая, когда в пластине имеется только один тип носителя тока, как в металле из-за отсутствия составляющей тока по оси Y, следует равенство нулю составляющей скорости по Y. Если в пластине имеется несколько типов носителей зарядов, как в полупроводнике, это условие уже не выполняется. В этом случае из равенства нулю составляющей тока по оси Y следует следующее равенство:

j_y = – ne ×< V_ye > + pe ×< V_yh > = 0, (4)

где < V_ye > – среднее значение проекции упорядоченной скорости электрона на ось Y; < V_yh > – среднее значение проекции упорядоченной скорости дырки на ось Y; n – концентрация электронов; p – концентрация дырок.

Для удобства описания таких процессов вводится величина называемая подвижностью носителя тока, определяемая как m = < V >/ E, где E – напряжённость электрического поля. Величина < V_ye > определяется проекцией напряжённости электрического поля на ось Y (E_y) и напряженности силы Лоренца (E_ly). Напряжённость силы Лоренца можно найти как E_ly = F _l/ e = < V_xe > B = m_e E_x B, где B – вектор магнитной индукции, действующий на пластину; m_e – подвижность электронов. Тогда по рис. 1, а можно видеть, что

< V_ye > = –m_e(E_y + E_ly) = –m_e E_y – m_e² В E_x. (5)

Аналогично для дырок:

< V_yh > = m _h (E_y – E_ly) = m _hE_y – m _h ² ВE_x, (6)

где m _h – подвижность дырок.

Подставим выражения (5) и (6) в выражение (4), получим:

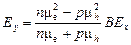. (7)

Постоянная Холла R = Uh /(IB) = E_ybh /(IB) = E_y /(jB) = E_y /(E_x s B), где s – удельная проводимость, для полупроводников определяемая по формуле s = e (n m_e + p m _h). Таким образом, для постоянной Холла в полупроводниках справедливо выражение:

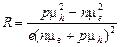. (8)

В случае собственного полупроводника n = p = n ₀ и

.

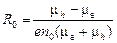Для случая акцепторного полупроводника n << p и в этом случае множителями, содержащими концентрацию электронов, можно пренебречь и из выражения (8) получим

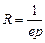. (9)

В этом случае подвижность носителей тока определяется как

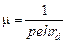. (10)

Причем, так как в этом случае носителем тока является положительный заряд, то знак холловской разности потенциалов определяется по рис. 1, а и противоположен знаку разности потенциалов для металлов.

Для случая донорного полупроводника p << n и в этом случае множителями, содержащими концентрацию дырок, можно пренебречь и из формулы (8) получим выражение (2). В этом случае знак холловской разности определяется по рис. 1, б и совпадает со знаком разности потенциалов для металлов.

Date: 2015-05-08; view: 607; Нарушение авторских прав