
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Числовые характеристики
|
|
Математическим ожиданием дискретной случайной величины называется:
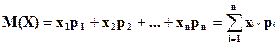
 (4.4)
(4.4)
В случае бесконечного множества значений 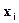 в правой части (4.4) находится ряд, и мы будем рассматривать только те значения Х, для которых этот ряд абсолютно сходится.
в правой части (4.4) находится ряд, и мы будем рассматривать только те значения Х, для которых этот ряд абсолютно сходится.
М(Х) представляет собой среднее ожидаемое значение случайной величины. Оно обладает следующими свойствами:
1) М(С)=С, где С=const
2) M (CX)=CM (X) (4.5)
3) M (X+Y)=M(X)+M(Y), для любых Х и Y. 
4) M (XY)=M (X)M(Y), если Х и Y независимы.
Для оценки степени рассеяния значений случайной величины около ее среднего значения M(X)= а вводятся понятия дисперсии D(X) и среднего квадратического (стандартного) отклонения 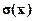 . Дисперсией называется математическое ожидание квадрата разности (X-
. Дисперсией называется математическое ожидание квадрата разности (X- 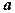 ), т.е.:
), т.е.:
D(X)=M(X- 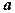 )2=
)2= 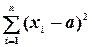 pi,
pi,
 где
где 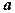 =М(X);
=М(X); 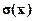 определяется как квадратный корень из дисперсии, т.е.
определяется как квадратный корень из дисперсии, т.е. 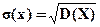 .
.
Для вычисления дисперсии пользуются формулой:
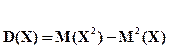 (4.6)
(4.6)
Свойства дисперсии и среднего квадратического отклонения:
1) D(C)=0, где С=сonst
2) D(CX)=C2D(X), 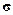 (CX)= çCç
(CX)= çCç 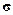 (X) (4.7)
(X) (4.7)
3) D(X+Y) =D(X)+D(Y), 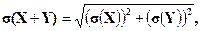
если Х и У независимы.
Размерность величин 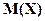 и
и 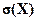 совпадает с размерностью самой случайной величины Х, а размерность D(X) равна квадрату размерности случайной величины Х.
совпадает с размерностью самой случайной величины Х, а размерность D(X) равна квадрату размерности случайной величины Х.
4.3. Математические операции над случайными величинами.
Пусть случайная величина Х принимает значения 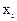 с вероятностями
с вероятностями 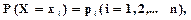 а случайная величина Y- значения
а случайная величина Y- значения 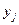 с вероятностями
с вероятностями 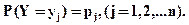 Произведение КX случайной величины Х на постоянную величину К - это новая случайная величина, которая с теми же вероятностями, что и случайная величина Х, принимает значения, равные произведениям на К значений случайной величины Х. Следовательно, ее закон распределения имеет вид таблица 4.2:
Произведение КX случайной величины Х на постоянную величину К - это новая случайная величина, которая с теми же вероятностями, что и случайная величина Х, принимает значения, равные произведениям на К значений случайной величины Х. Следовательно, ее закон распределения имеет вид таблица 4.2:
Таблица 4.2
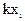
| 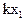
| 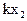
| ... | 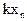
|
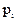
| 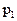
| 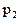
| ... | 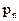
|
Квадрат случайной величины Х, т.е. 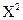 , - это новая случайная величина,которая с теми же вероятностями, что и случайная величина Х, принимает значения, равные квадратам ее значений.
, - это новая случайная величина,которая с теми же вероятностями, что и случайная величина Х, принимает значения, равные квадратам ее значений.
Сумма случайных величин Х и У - это новая случайная величина, которая принимает все значения вида 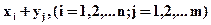 с вероятностями
с вероятностями 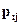 , выражающими вероятность того, что случайная величина Х примет значение
, выражающими вероятность того, что случайная величина Х примет значение 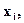 а У - значение
а У - значение 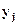 , то есть
, то есть
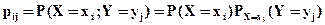 (4.8)
(4.8)
Если случайные величины Х и У независимы, то:
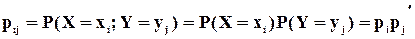 (4.9)
(4.9)
Аналогично определяются разность и произведение случайных величин Х и У.
Разность случайных величин Х и У - это новая случайная величина, которая принимает все значения вида 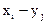 , а произведение - все значения вида
, а произведение - все значения вида 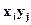 с вероятностями, определяемыми по формуле (4.8), а если случайные величины Х и У независимы, то по формуле (4.9).
с вероятностями, определяемыми по формуле (4.8), а если случайные величины Х и У независимы, то по формуле (4.9).
4.4. Распределения Бернулли и Пуассона.
Рассмотрим последовательность n идентичных повторных испытаний, удовлетворяющих следующим условиям:
1. Каждое испытание имеет два исхода, называемые успех и неуспех.
Эти два исхода - взаимно несовместные и противоположные события.
2. Вероятность успеха, обозначаемая p, остается постоянной от испытания к испытанию. Вероятность неуспеха обозначается q.
3. Все n испытаний - независимы. Это значит, что вероятность наступления события в любом из n повторных испытаний не зависит от результатов других испытаний.
Вероятность того, что в n независимых повторных испытаниях, в каждом из которых вероятность появления события равна 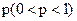 , событие наступит ровно m раз (в любой последовательности), равна
, событие наступит ровно m раз (в любой последовательности), равна
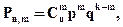 (4.10)
(4.10)
где q=1-р.
Выражение (4.10) называется формулой Бернулли.
Вероятности того, что событие наступит:
а) менее m раз,
б) более m раз,
в) не менее m раз,
г) не более m раз - находятся соответственно по формулам:

Биномиальным называют закон распределения дискретной случайной величины Х - числа появлений события в n независимых испытаниях, в каждом из которых вероятность наступления события равна р; вероятности возможных значений Х = 0,1,2,..., m,...,n вычисляются по формуле Бернулли (таблица 4.3).
Таблица 4.3
| Число успехов Х=m | ... | m | ... | n | |||
Вероятность Р 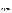  
|
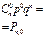
|
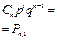
|
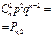
| ... |
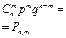
| ... |
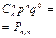
|
Так как правая часть формулы (4.10) представляет общий член биноминального разложения 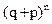 , то этот закон распределения называют биномиальным. Для случайной величины Х, распределенной по биноминальному закону, имеем:
, то этот закон распределения называют биномиальным. Для случайной величины Х, распределенной по биноминальному закону, имеем:
M(X)=nр (4.11)
D(X)=nрq (4.12)
Если число испытаний велико, а вероятность появления события р в каждом испытании очень мала, то вместо формулы (4.10) пользуются приближенной формулой:
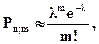 (4.13)
(4.13)
где m - число появлений события в n независимых испытаниях, 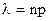 (среднее число появлений события в n испытаниях).
(среднее число появлений события в n испытаниях).
Выражение (4.13) называется формулой Пуассона. Придавая m целые неотрицательные значения m=0,1,2,...,n, можно записать ряд распределения вероятностей, вычисленных по формуле (4.13), который называется законом распределения Пуассона (таблица 4.4):
Таблица 4.4
| M | ... | m | ... | n | |||
| Pn;m | 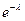
| 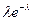
| 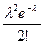
| ... | 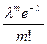
| ... | 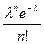
|
Распределение Пуассона часто используется, когда мы имеем дело с числом событий, появляющихся в промежутке времени или пространства. Например, число машин, прибывших на автомойку в течении часа, число дефектов на новом отрезке шоссе длиной в 10 километров, число мест утечки воды на 100 километров водопровода, число остановок станков в неделю, число дорожных происшествий.
Если распределение Пуассона применяется вместо биномиального распределения, то n должно иметь порядок не менее нескольких десятков, лучше нескольких сотен, а nр< 10.
Математическое ожидание к дисперсии случайной величины, распределенной по закону Пуассона, совпадают и равны параметру 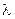 , которая определяет этот закон, т.е.
, которая определяет этот закон, т.е.
M(X)=D(X)=n×p= 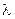 . (4.14)
. (4.14)
Date: 2015-05-08; view: 806; Нарушение авторских прав