Трение. Вязкость — внутреннее трение

Трение — широко распространенное явление. Трение при соприкосновении твердых тел характеризуется коэффициентом трения скольжения (рис. 4.5, a). В курсах теоретической механики изучают еще и трение качения (как всегда все сводится к связи поступательного и вращательного движений). В жидкостях и газах тела при движении испытывают вязкое трение (рис. 4.5, б). Важно, что всякая сила трения связана со скоростью. Сила трения направлена противоположно скорости. Сила вязкого трения еще вдобавок и по величине пропорциональна скорости.

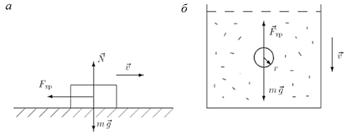
Рис. 4.5. Сила трения, действующая на движущееся тело: а — сила трения скольжения F _тр = μ N, μ — коэффициент трения (скольжения); б — сила вязкого трения F _тр = γ V = η AV, γ — коэффициент трения (вязкого трения), η — коэффициент вязкости. Для шара величина А = 6π r и F _тр = 6πη rV

Так как силы трения зависят от скорости, то они не консервативны. Работа этих сила изменяет внутреннюю энергию «трущейся пары», а не служит для преобразования кинетической и потенциальной энергий тела друг в друга, как работа консервативных сил (упругости, тяготения, кулоновской). Отметим, что неконсервативной является и сила давления газа F = рS, ведь давление газа (или жидкости) связано с молекулярными движениями, например, в газе давление пропорционально среднему квадрату скорости р ~ á V 2ñ.

Таким образом, явления, связанные с трением, находятся в связи и с механикой (скорость), и с молекулярной физикой (работа сил трения дает изменение внутренней энергии). Такая двойственность приводит к изменениям в трактовке некоторых положений механики. Например, неприменимым становится положение об относительности покоя и движения. Когда действуют только консервативные силы, то невозможно различить равномерное движение или покой. Относительно Земли — покоимся (Кто не крутится на своем месте!), а относительно Солнца? Другое дело, если в игре есть и силы трения. Тогда при движении (даже равномерном) выделяется теплота. При учете сил трения равновесие сил наступает только при движении.

В конечном итоге это изменение возникает из-за того, что, согласно второму закону Ньютона, результат силы — ускорение, но сила трения может изменять равнодействующую силу так, что наступит равновесие и ускорения не будет. Именно путаница в этом вопросе не позволила открыть законы механики древним. Аристотель видел: две лошади — одна скорость повозки; три лошади — больше скорость повозки, следовательно, делал вывод Аристотель, скорость пропорциональна числу «лошадей», или пропорциональна силе тяги, или, вообще, пропорциональна силе. Аристотель считал, что скорость пропорциональна силе. В действительности, при увеличении силы тяги ускорение появляется, но из-за увеличения скорости увеличивается и сила трения, и очень быстро наступает равновесие при этой новой скорости. Аристотель перехода не видел. Во множестве других случаев «закон Аристотеля» не соответствовал наблюдениям. Кто движет планеты? Где лошади? Ньютон сделал «наукой» механику, когда сумел объединить и «земные», и «небесные» движения. Аристотель умел объяснять только «земные».

Возвращаясь к явлениям трения, можно сказать, что в этих явлениях всегда есть выделенная система отсчета — та, «обо что трется» тело, и силы трения зависят именно от скорости движения относительно этой системы. Сила трения «переводит» энергию движения во внутреннюю энергию именно тела (среды), о которое трется движущееся тело, и тем самым выделяет его, выделяет из всех других тел.

Итак, если силы консервативны — все движущиеся друг относительно друга с постоянными скоростями системы отсчета (они называются инерциальными) равноправны, покой и движение с постоянной скоростью — относительны. Если силы не консервативны — зависят от скорости, то есть выделенная система отсчета — та, во внутреннюю энергию которой переходит энергия движения. Теперь покой и движение относительно этой выделенной системы можно легко различить. Если есть «перекачка» энергии движения во внутреннюю — есть движение, нет перекачки — покой.

Рассматривая только трение при движении в жидкости или газе, используют характеристику такого явления, называемую коэффициентом вязкости, часто говорят — просто вязкость η. Вязкость характеризует именно свойства среды — жидкости или газа. Отсюда следует, что вязкость не зависит от свойств движущегося тела (размеров или скорости, или еще чего-нибудь), а зависит только от характеристик среды (давления, температуры, либо еще каких-то), в которой происходит движение. В конечном итоге коэффициент вязкости зависит от свойств молекул среды, в которой движется тело.

Эти свойства легче всего выявить, рассматривая явление внутреннего трения. Действительно, не все ли равно, движется тело относительно газа (жидкость) или одна часть жидкости (газа) движется относительно другой. И в том, и в другом случае должно наблюдаться явление перекачки энергии макроскопического движения (движения чего-то «большого» — тела или части жидкости) во внутреннюю энергию — движения молекул — микроскопических (малых) частиц.

Явление внутреннего трения (часто называемое явлением вязкости) связано с возникновением сил трения между слоями газа или жидкости, перемещающимися параллельно друг другу с различными по величине скоростями, при этом происходит выравнивание скоростей. Силы трения, которые при этом возникают, направлены по касательной к поверхности соприкосновения слоев.

Рассмотрим механизм вязкости газов. Почему соседние слои тормозят друг друга при своем движении? Следующая модель поможет разобраться в этом: представим лодки, движущиеся вниз по реке с разными скоростями (рис. 6.6).

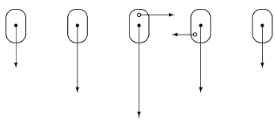
Рис. 4.6. К объяснению механизма вязкости. Подробности в тексте

Чем ближе лодки к центру реки, тем больше стараются гребцы. На лодках перевозят арбузы. Торговки решают обменяться товаром. Арбузы имеют скорость лодки, в которой они находятся. Поэтому при перебрасывании «быстрых» арбузов в медленно движущиеся лодки последние ускоряются; быстрые же лодки замедляют свое движение при попадании в них медленно движущихся арбузов.

Явление внутреннего трения подчиняется закону Ньютона для вязкого трения(часто готворят и «формула Ньютона для вязкого трения»):

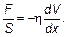(4.33)

После всего сказанного эта формула кажется составленной просто «руками». Действительно: коэффициент вязкости η показывает происхождение этой силы от «трения», dV / dx показывает изменение скорости движения слоев друг относительно друга, ведь dV / dx изменение скорости на единицу длины — это предел от (V 2 – V 1)/(x 2 – х 1). Очевидно, что формула Ньютона имеет вид уравнения переноса (тип закона Фика) (4.13). Справа — производная (градиент), слева должен быть поток. Поток — это что-то протекающее через единицу площади S в единицу времени Δ t. Площадь на нужном месте в формуле есть — стоит F / S. Следовательно, хорошо бы представить и силу как производную от «чего-то» по времени. Вспоминая второй закон Ньютона, можно увидеть, что силу можно представить как

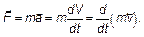(4.34)

То есть сила есть производная от импульса .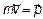

Таким образом, формула Ньютона — формула для переноса импульса. На молекулярном уровне отсюда следует, что трение между текущими (движущимися) с разными скоростями слоями жидкости или газа состоит в передаче молекул от слоя с большей скоростью в слой с меньшей скоростью (рис. 4.7).

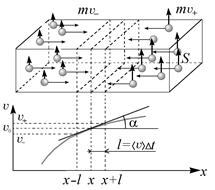
Рис. 4.7. К объяснению закона вязкости. V ₊ = V ₀ + D V = V + l tgα

Все явления переноса в газе аналогичны. Это наглядно видно из соответствующих рисунков (сравните рис. 4.2, 4.4 и 4.7). Диффузии соответствует разность концентраций, теплопроводности — разность внутренних энергий, внутреннему трению (вязкости) — разность скоростей в перпендикулярном силе трения (потоку импульса) направлении. Объемы же, из которых молекулы за время Δ t успевают поменять «место жительства», одинаковы. Поэтому, рассчитывая поток, так же как это делалось уже дважды, найдем поток импульса:

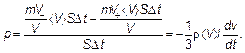(4.35)

Сравнивая с формулой Ньютона, найдем, что коэффициент вязкости имеет вид:

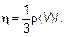(4.36)

Эта формула хороша для газов и позволяет анализировать зависимости коэффициента вязкости от параметров газа. Для жидкостей — коэффициент вязкости — характеристика жидкости приводится в справочниках.

Часто вместо коэффициента вязкости вводят так называемый коэффициент кинематической вязкости:

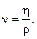(4.37)

В итоге закон трения (закон Ньютона) имеет форму

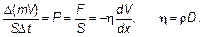(4.38)

Величина Р — поток импульса.

Подводя итоги изучения сил вязкого трения, отметим еще раз, что сила, действующая на «тело», пропорциональна скорости V, а сила, действующая на «слой», пропорциональна производной от скорости dV / dx. Для жидкостей с большой вязкостью, когда отдельный слой превращается как бы в «плоское тело», это различие несущественно. Действительно, в таких условиях:

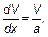(4.39)

где а — толщина пограничного слоя, толщина жидкости, на которой значительно меняется скорость.

Силу вязкого трения, создаваемую движущимся в жидкости или газе телом (рис. 4.5, б), называют силой Стокса. Тело приводит в движение жидкость перед собой, а вдали от тела жидкость покоится. Так возникает разность скоростей между слоями. Запись силы Стокса (формула Стокса) получается прямо из закона Ньютона для вязкого трения (4.33). Применим метод анализа размерностей.

Производную в этой формуле заменим величиной той же размерности V / a, где а — как обычно (см. формулу (4.39)), толщина жидкости, на которой значительно меняется скорость. После такой замены в законе Ньютона для силы вязкого трения возникает величина S / a, имеющая размерность длины (м). В решаемой задаче имеется только одна величина такой размерности, это размер тела. Если тело — шар, то это радиус шара r (см. рис. 4..5, б). Теперь, когда все размерные зависимости определены, остается неопределенным числовой множитель. Оказывается, что этот множитель зависит от формы тела. Для шара он равен 6π. Получаем окончательно формулу Стокса:

F = 6π r η V. (4.40)

Date: 2015-05-08; view: 1503; Нарушение авторских прав