Диффузия как случайное блуждание

Закон Фика говорит лишь о приросте числа частиц (или массы), который происходит при рассматриваемом процессе переноса — диффузии. Часто, однако, важно знать и расстояние (конечно, среднее), на которое проникнут молекулы одного вещества в другое за какое-то время t.

В силу беспорядочности движения молекула продвигается в нужном (выделенном) направлении лишь случайно, поэтому такое движение называется случайным блужданием.

Рассмотрим случайное блуждание вдоль прямой (рис. 4.3). Это такое движение, при котором молекула может двигаться только вправо или влево, а конкретное направление выбирается случайно, например, подбрасывание монеты: выпадает орел — идет вправо, решка — влево.

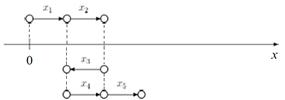
Рис. 4.3. Случайное блуждание на прямой

Ясно, что при «одном движении» молекула продвигается (в среднем) на расстояние, равное длине свободного пробега. Так как вероятность, что молекула сдвинется вправо (на + l) такая же, как и вероятность движения влево (на – l), то при большом числе N таких движений

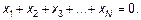(4.15)

Каждой «положительной» xi = l найдется своя отрицательная xk = – l.

Отсюда следует, что среднее смещение (алгебраическая сумма) равно нулю:

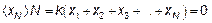(4.16)

Точно такая же ситуация была и со средней скоростью хаотического движения, которая рассматривалась при выводе основного уравнения молекулярно-кинетической теории.

Займемся теперь вычислением средних квадратов смещений. Очевидно, что

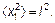(4.17)

Для следующего шага х 2 = х 1 ± l имеем в среднем

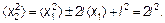(4.18)

Использовались, во-первых, предыдущая формула, а во-вторых, что среднее значение, как только что было установлено (см. формулу (4.16)), равно нулю. Так можно делать и дальше для третьего, четвертого и т. д. шагов:

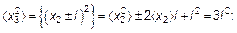(4.19)

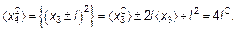(4.20)

Возникает естественный результат, а именно средний квадрат смещения равен

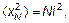(4.21)

где N — число шагов. Эта формула подобна формуле для внутренней энергии 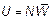, где 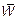= m 0á V 2ñ/2 определяется средним квадратом скорости.

Свяжем теперь число шагов N со временем t, за которое они совершены. Для этого нужно ввести время одного шага τ. В среднем τ = t / N. С другой стороны, среднее время одного смещения (шага) τ можно определить из длины свободного пробега:

l = á V ñτ. (4.22)

Время τ — это время между двумя столкновениями (на прямой это время между двумя поворотами). Число столкновений в единице времени

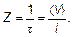(4.23)

Подставляя N = t /τ в формулу среднего квадрата смещения, получим

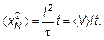(4.24)

Отсюда видно, что коэффициент пропорциональности между средним квадратом смещения (но не квадратом среднего смещения, который равен нулю) и временем, за которое это смещение происходит, является коэффициентом диффузии

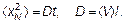(4.25)

Среднее (среднеквадратичное) смещение молекулдиффузией 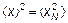будет

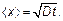(4.26)

Числовой множитель определяется «размерностью» пространства, в котором происходят блуждания. При блужданиях на плоскости будет D = á V ñ l /2, а в трехмерном пространстве пришли бы к выведенному ранее значению D = á V ñ l /3.

Полученная формула позволяет оценить, насколько отклонится от начального положения точка при случайном блуждании.

Обычный «пешеход» продвигается не спеша с V = 3,6 км/час = 1 м/с, но широким шагом l = 1 м. За t = 1 ч пешеход уйдет на расстояние х = 3600 м, т. е. далеко. Но не очень «трезвый» гражданин, совершая случайные блуждания на плоскости, уйдет в случайном направлении на расстояние 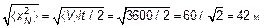. Это не далеко. Именно в соответствии с формулой, описывающей случайные блуждания, медленно распространяются запахи, хотя скорости движения молекул огромны. Как говорится, на кухне все давно сгорело, а в комнате еще и не пахнет жареным. Почему? По законам диффузного движения — случайных блужданий.

Date: 2015-05-08; view: 1067; Нарушение авторских прав