Распределение Максвелла

Распределение Максвелла — это распределение молекул по модулю, по величине скорости. Так как по величине скорость определяется тремя ее проекциями, а проекции могут иметь независимые значения, то согласно правилу перемножения вероятностей (см. п. 3.3) имеем:

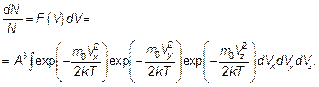(3.24)

Конечно, при записи этой формулы использован и принцип (распределение) Больцмана. Распределение по направлениям может быть «уничтожено» интегрированием по углам θ и φ, определяющим направление вектора скорости. Очевидно, что

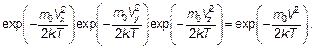(3.25)

Этот результат можно было предвидеть в соответствии с законом Больцмана. Ведь W к = m 0 V 2/2.

Теперь выразим dVxdVydVz через модуль скорости и углы, задающие ее направление. Для этого используем, что произведение dxdydz — это элемент объема («малый объем»). Также и dVxdVydVz — малый объем в пространстве скоростей.

Переход от Vx; Vy; Vz — проекций скоростей в декартовых координатах (см. рис. 3.5 и 3.9) к модулю скорости 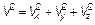и углам θ и φ совершенно аналогичен переходу от декартовых координат х; у; z к сферическим координатам с расстоянием r 2 = х 2 + у 2 + z 2и теми же углами θ и φ (рис. 3.10).

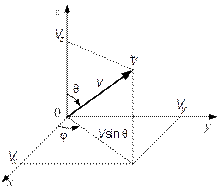
Рис. 3.9. Переход от проекций скоростей Vx; Vy; Vz к модулю скорости V

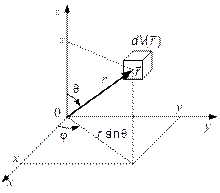
Рис. 3.10. Переход от декартовых координат x, y, z к сферическим r, θ, φ

Сравнивая рис. 3.9 и 3.10, видим, что переход от элемента объема в пространстве скоростей в декартовых координатах dVxdVydVz, к элементу объема также в пространстве скоростей, 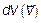, но выраженному через модуль скорости V и углы θ и φ, полностью аналогичен (совпадает!) с переходом от элемента объема в декартовых координатах dxdydz (рис. 3.11) к элементу объема 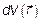в сферических координатах (рис. 3.12)

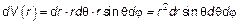(3.26)

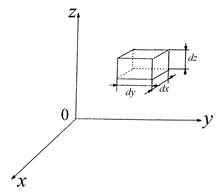
Рис. 3.11. Элемент объема dxdуdz в декартовой системе координат. В пространстве скоростей ему соответствуют dVxdVydVz

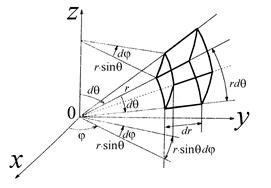
Рис. 3.12. Элемент объема dr ⋅ rd θ ⋅ r sinθ d φ в сферических координатах.
В пространстве скоростей ему соответствует dV ⋅ Vd θ ⋅ V sinq d φ

Очевидно, что для перехода от «пространства координат» к «пространству скоростей» (см. рис. 3.12) нужно заменить х на Vх, у на Vу, z на Vz, радиус-вектор 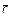на вектор скорости 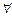, а радикальную координату 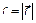на модуль скорости 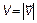. Тогда элемент объема в пространстве скоростей dVxdVydVz преобразуется в

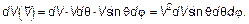(3.27)

Легко провести интегрирование по углам.

Интегрируем

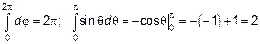(3.28)

и записываем формулу, позволяющую вычислить вероятность, что молекула имеет скорость с величиной, лежащей в интервале между V и V + dV.

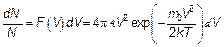(3.29)

Распределение вероятности имеет вид (рис. 3.13):

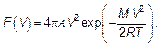(3.30)

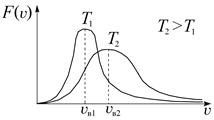
Рис. 3.13. Распределение Максвелла

Именно это распределение и называется распределением Максвелла. Количество молекул, имеющих скорость, лежащую между V и V + dV, будет:

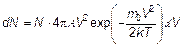(3.31)

а функция распределения количества молекул, соответственно,

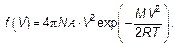(3.32)

Как видно из формулы (3.30), вид кривой распределения зависит от природы молекул (в формулу входит молярная масса М) и от температуры. На рис. 3.14 приведены кривые распределения молекул азота по скоростям при различных температурах. При повышении температуры вся кривая смещается в сторону больших скоростей (положение максимума, т. е. V нвпропорционально 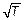). Площади под этими кривыми остаются, конечно, неизменными и равными единице, ведь это сумма всех вероятностей того, что молекулы имеют хоть какую-нибудь скорость. Вследствие этого максимум кривой при повышении температуры уменьшается.

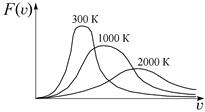
Рис. 3.14. Распределение Максвелла для данного газа при нескольких температурах

Date: 2015-05-08; view: 908; Нарушение авторских прав