Расчет момента инерции маятника

Пока сила тяжести Р, приложенная в центре масс С, направлена вдоль оси стержня (рис. 5.1, а), система находится в равновесии. Если отклонить стержень на некоторый малый угол 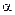(рис. 5.1, б), то центр масс С поднимается на небольшую высоту и тело приобретает запас потенциальной энергии. На маятник относительно оси О, направление которой выбираем «к нам», будет при этом действовать момент силы тяжести, проекция которого на эту ось равна

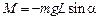, (5.1)

где 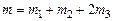; L – расстояние между осью вращения О и центром масс С.

Вращающий момент М, создаваемый силой Р, при малых углах 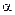равен

.

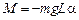Он вызывает ускорение при вращательном движении маятника. Связь между этим ускорением и моментом сил дается основным уравнением динамики вращательного движения

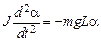, (5.2)

где J – момент инерции маятника относительно оси О.

Обозначим

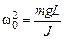. (5.3)

Тогда из уравнения (5.2) получим

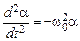. (5.4)

Уравнение (5.4) описывает колебательный процесс с циклической частотой .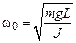

Период колебаний, следовательно, равен

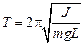. (5.5)

Из формулы (5.5) выразим момент инерции

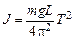. (5.6)

Если положение центра масс системы не изменяется, то величина L постоянна и в формулу (5.6) можно ввести постоянный коэффициент

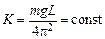. (5.7)

Измеряя время t, в течение которого происходит n полных колебаний, найдем период 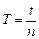. Подставляя T и K в (5.6), получаем рабочую формулу

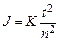. (5.8)

С помощью формулы (5.8) производятся косвенные измерения момента инерции физического маятника относительно оси О.

С другой стороны, момент инерции J зависит от положения грузов 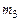на стержне. Переместим грузы 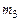по стержню так, чтобы они располагались симметрично относительно некоторой точки А. Эта математическая точка выбрана произвольно вблизи середины стержня. Центр масс системы при этом сохраняет свое местоположение. Будем считать размеры грузов 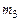малыми по сравнению с 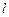и 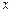(см. рис. 5.1). Тогда их можно рассматривать как материальные точки. В этом случае момент инерции системы определяется выражением

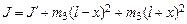, (5.9)

где 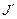– момент инерции системы без грузов; x – расстояние груза 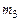до точки А; l – расстояние точки А до оси вращения маятника О.

Преобразуя формулу (5.9), получаем

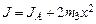, (5.10)

где 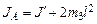– момент инерции маятника при положении грузов 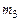в точке А.

Зависимость (5.10) будем проверять, получая величины J и J_A экспериментально с помощью формулы (5.8).

Date: 2015-05-08; view: 718; Нарушение авторских прав