Лабораторная работа Определение радиуса кривизны линзы с помощью колец Ньютона

Ц е л ь р а б о т ы: изучить явление интерференции света на тонких пленках; научиться определять радиус кривизны линзы с помощью полос равной толщины.

Приборы и принадлежности: микроскоп МБС-10 со столиком,
плоско-выпуклая линза, плоско-параллельная пластинка, осветитель с блоком
питания, светофильтры.

3.2.1. Описание экспериментальной установки и метода

Частным случаем интерференции на тонких пленках являются кольца Нью­тона. Направим пучок монохроматического света параллельно главной оптичес­кой оси плосковыпуклой тонкой линзы, лежащей на стеклянной пластинке. Если радиус кривизны линзы большой, то луч 1 (рис. 1),.отраженный от прослойки, находящейся между линзой и пластинкой, и луч 2, отраженный от поверхности

пластинки, являются когерентными, а следовательно, будут интерферировать

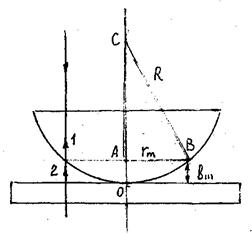
Рис. 1

При нахождении оптической разности хода когерентных лучей можно пренебречь небольшими наклонами лучей, проходящих в прослойке. Геометри­ческая разность хода между когерентными лучами, очевидно, равна 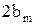, где - толщина зазора в данном месте.

Для вычисления полной оптической разности хода лучей необходимо учесть оптические свойства прослойки (показатель преломления), а также изме­нение фазы световой волны. При отражении световой волны от оптически более плотной среды фаза электрического вектора изменяется на .

Таким образом, если 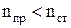, то луч 2 меняет фазу, а для случая 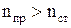меняет фазу луч 1. Но в обоих случаях происходит сдвиг фазы на 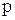следовательно,

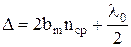(1)

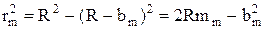(2)

Принимая во внимание, что 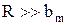, получим:

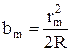(3)

С учетом (3) выражение (1) примет вид:

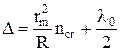(4)

Из выражения (1) видно, что оптическая разность хода при заданной длине волны определяется полностью толщиной прослойки. Значит, наблюдаемые ин­терференционные полосы являются полосами равной толщины, а в соответствии с (4) они представляют собой кольца радиуса 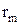с центром в точке соприкоснове­ния линзы с пластинкой (точка 0 на рис. 1).

Радиусы темных колец найдем из условия минимума:

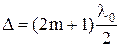(5)

Приравняв правые части равенств (4) и (5), получим

(6)

Для радиусов светлых колец аналогично получим

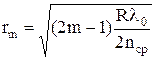(7)

Если линза и пластинка имеют одинаковый показатель преломления, то центр колец в отраженном свете темный. Так как прослойка представляет собой клин с изменяющимся преломляющим углом, то кольца сгущаются по мере уве­личения угла.

Экспериментальная установка состоит из микроскопа МБС 10, в комплект которого входят осветительная лампа с конденсором и блоком питания, а также плоско-параллельная пластинка с выпуклой линзой, закрепленные имеете в пласт­массовом кольце. Степень прижатия линзы к пластинке регулируется резьбой кольца.

В работе рекомендуется использовать окуляр 8 в фокальной плоскости которого установлена плоско-параллельная пластинка со шкалой с пеной деления 0.1 мм.

В переводной таблице указано, какой величине объекта соответствует одно деление шкалы при всех увеличениях микроскопа:

Для создания параллельного пучка лучей, падающих нормально на систе­му линза-пластинка, осветитель устанавливается в одну из окулярных трубок би­нокулярной насадки.

Измерив радиусы светлых и темных колец, можно рассчитать длину волны 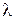, если известен радиус кривизны линзы 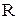. И наоборот, по известному значе­нию 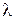можно определить радиус кривизны линзы 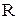. Поскольку практически никогда не удается получить соприкосновение линзы с пластинкой без зазоров, то для получения более точного результата в определени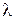и или 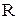следует вос­пользоваться графическим методом обработки экспериментальных данных, ко­торый изложен ниже.

Записав выражения для 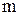- го и 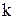- гo темных колец и вычтя их друг из друга, получим при интерференции на воздушной прослойке ():

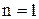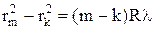(8)

Аналогично для светлых колец:

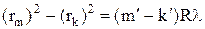(9)

Значения радиусов 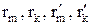необходимо брать из графика зависимости 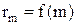, построенного по результатам измерений. Как следует из (8) и (9), графики зависимости квадрата радиуса кольца от его номера должны иметь линейный ха­рактер. Практически при измерении всегда допускаются ошибки, кроме того, де­формация линзы и стеклянной пластинки в местах их соприкосновения может при­водить к отступлению от формул (8) и (9). Поэтому к результатам, полученным при малых номерах колец, следует относиться с осторожностью. Так как меньше искажены влиянием деформации кольца Ньютона с большими номерами, то после нанесения экспериментальных точек необходимо проводить прямую 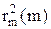пре­имущественно по точкам для больших номеров колец.

Date: 2015-05-08; view: 916; Нарушение авторских прав