Тема 3. Явление электромагнитной индукции. Самоиндукция

Теоретическое введение к лабораторной работе №28

В 1831 году М. Фарадеем было открыто явление электромагнитной индукции. Оно заключается в том, что в замкнутом проводящем контуре при изменении магнитного потока Ф через поверхность, ограниченную этим контуром, возникает электрический ток, который назвали индукционным.

Магнитный поток 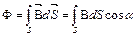, (3.1)

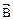где В - индукция магнитного поля, dS-площадь элемента поверхности, -угол между вектором и нормалью к площадке dS. Индукционный ток возникает при изменении любой из величин, входящих в формулу (3.1). Появление индукционного тока означает, что при изменении магнитного потока в контуре возникает ЭДС индукции 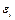. Опытным путём было установлено, что величина ЭДС индукции зависит только от скорости изменения магнитного потока, т.е. от величины .

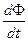Направление индукционного тока (а значит и знак 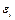) определяется правилом Ленца: индукционный ток всегда направлен так, чтобы противодействовать причине, его вызывающей. Иначе говоря, индукционный ток создает магнитный поток, препятствующий изменению магнитного потока, вызывающего ЭДС индукции. Закон электромагнитной индукции имеет вид:

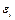
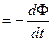. (3.2)

Знак минус в правой части уравнения соответствует правилу Ленца.

Если замкнутый контур, в котором индуцируется ЭДС, состоит не из одного витка, а из N витков (например, катушка), то 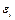будет равна сумме ЭДС, индуцируемых в каждом из витков. Если магнитный поток, охватываемый каждым витком, одинаков и равен Ф, то суммарный поток сквозь поверхность, натянутую на такой сложный контур, равен

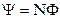. (3.3)

Эту величину называют полным магнитным потоком или потокосцеплением.

В этом случае формула (3.2) примет вид 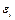. (3.4)

Причины появления 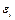различны. Если изменение магнитного потока вызвано изменением площади, при постоянных индукции магнитного поля и угле , то сторонней силой, обеспечивающей появление индукционного тока, является сила Лоренца 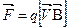. (3.5)

Рассмотрим контур с подвижной перемычкой длиной  (рис. 3.1)

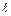	Рис. 3.1

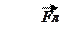Пусть он находится в однородном магнитном поле с индукцией 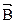(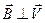). Если перемычку двигать вправо с постоянной скоростью 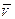, то с такой же скоростью будут двигаться и свободные электроны. На каждый электрон начнет действовать вдоль перемычки сила Лоренца, и они начнут перемещаться по перемычке вниз, т.е. потечёт электрический ток, направленный вверх. Это и есть индукционный ток, а ЭДС индукции

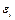
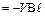. (3.6)

Если проводящий контур неподвижен и =const, а меняется индукция магнитного поля то, как показал Максвелл, индукционный ток обусловлен возникающим в проводнике вихревым электрическим полем 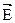, и ЭДС индукции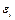 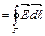согласно формуле (3.2) будет равна

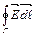
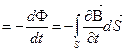. (3.7)

(полную производную заменили частной, т.к. индукция магнитного поля может зависеть не только от времени, но и координат).

Если в некотором контуре течёт изменяющийся во времени ток, то магнитное поле этого тока также будет изменяться. Это влечёт изменение магнитного потока сквозь поверхность, ограниченную этим контуром, а следовательно и появление в нём ЭДС индукции.

Таким образом, изменение тока в контуре ведет к возникновению ЭДС индукции в этом же самом контуре. Это явление называется самоиндукцией.

Сила тока в контуре связана с охватываемым им собственным полным магнитным потоком формулой

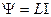, (3.8)

где коэффициент L называется индуктивностью контура. Индуктивность зависит от формы, размеров контура и магнитных свойств окружающей его среды.

ЭДС самоиндукции найдем, подставив (3.8) в (3.4)

.

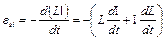Если при изменениях силы тока индуктивность L остается постоянной (не меняется конфигурация контура и нет ферромагнетиков), то .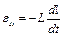

Знак минус показывает, что 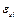всегда направлена так, чтобы препятствовать изменению силы основного тока. Она противодействует току, когда он увеличивается, и поддерживает ток, когда он уменьшается.

i. Ферромагнетики

Ферромагнетиками называются твёрдые вещества, которые могут обладать самопро-извольной (спонтанной) намагниченностью, т.е. остаются намагниченными при отсутствии внешнего магнитного поля. Типичные представители ферромагнетиков – это железо, кобальт, никель и многие их сплавы.

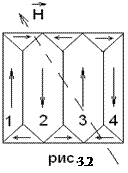
Физическую природу ферромагнетизма удалось понять только с помощью квантовой механики. При определённых условиях в кристаллах могут возникать так называемые обменные силы, которые заставляют магнитные моменты электронов устанавливаться параллельно друг другу. В результате возникают области (размером 1-10 мкм) спонтанного, т.е. самопроизвольного, намагничивания – эти области называются доменами (рис. 3.2). Разбиение ферромагнетика на домены происходит потому, что при этом энергия ферромагнетика уменьшается.

В пределах каждого домена ферромагнетик намагничен до насыщения и имеет определённый магнитный момент.

Направления этих моментов для различных доменов различны, поэтому при отсутствии внешнего поля суммарный момент образца равен нулю и образец в целом макроскопически ненамагничен. Действие внешнего поля на домены на разных стадиях процесса намагничивания оказывается различным.

Вначале, при слабых полях, наблюдается смещение границ доменов, в результате чего происходит увеличение тех доменов, моменты которых составляют с вектором напряженности магнитного поля 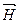меньший угол (1 и 3), за счет энергетически менее выгодных доменов, у которых этот угол больше (2 и 4). С ростом 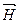этот процесс идёт всё дальше и дальше, пока домены с меньшим углом не поглотят целиком остальные домены. На следующей стадии происходит поворот магнитных моментов доменов в направлении поля. В этом состоянии ферромагнетик будет иметь наибольший магнитный момент, что соответствует состоянию насыщения.

Эти процессы (исключая небольшие смещения границ между доменами в очень слабых полях) являются необратимыми, и служат причиной гистерезиса.

2. Цепи с ферромагнитными сердечниками при постоянном магнитном потоке(I=const)

Примерная графическая зависимость 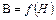для ферромагнитных материалов показана на рис. 3.3.

Если довести намагничивание до насыщения (точка 1 на рис. 3.3), а затем уменьшить H, то индукция уменьшится не по первоначальной кривой, а по кривой 1-2-3 и т.д.

Такая зависимость называется петлёй гистерезиса. При возрастании напряженности магнитного поля Н индукция В возрастает по нижней части петли, а при убывании H индукция B уменьшается по верхней части петли. Индукция Br при H=0 называется остаточной. Ширина петли в основном зависит от свойств материала. Ширина петли равна 2Hс, где Нс – коэрцитивная сила. Ферромагнитные материалы с широкой петлей гистерезиса (Hс>4000A/м) называют магнитно-твердыми. Их применяют для изготовления постоянных магнитов. Ферромагнитные материалы с узкой петлёй гистерезиса (Hс<200A/м) называют магнитно-мягкими. Их применяют в переменных магнитных полях.

Если построить для большого числа постепенно возрастающих максимальных напряженностей H_max какого-либо магнитно-мягкого материала семейство статических петель гистерезиса, то вершины петель располагаются на кривой, называемой основной кривой намагничивания данного материала (рис. 3.4).

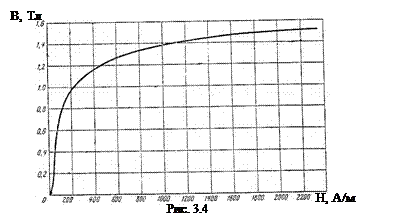Зная H, по графику можно определить магнитную проницаемость 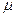материала.

Date: 2015-05-08; view: 935; Нарушение авторских прав