Коллоидты ерітінділердің тұтқырлығы

Сұйық күйіндегі коллоидты ерітінділерге ағу және тұтқырлық қасиеттер тән. Жалпы тартылыс дүниеліктерінің ағу қасиетіне ие болуын, пішін келбетін өзгертіп деформациялануын зерттейтін ғылым саласы реология деп аталады.

Сұйық заттарға тән ағу және тұтқырлық – реология қасиеттерінің бір көріністері.

Бір сәт тастан тасқа аққан тау өзені мен жазық далада жайбарақат ағып жатқан суды көз алдыңызға елестетіңізші. Алғашқысы буырқанып, сапырылысып көбіктеніп, кей тұстары иірім жасап ағады.

Сұйықтың буырқанып, құйындай үйіріліп, иірім жасай сапырылысып ағуы – турбулентті ағыс деп аталады.

Сұйықтың тып – тыныш, өз қабатымен жайбарақат ағуы – ламинарлық ағыс деп аталады.

Сұйық бойында оның молекулалары өзара молекулаарлық күштермен байланысқан. Сондықтан сұйықтың бір қабаты екінші бір қабатына қарағанда ағып, орын ауыстыру барысында міндетті түрде әлгі сұйық молекулаларының байланыс күшін, яғни кедергісін сезінеді.

Сұйық қабаттарының ағу барысында өзара бір – біріне іштей үйкеліс нәтижесінде кедергі келтіруін, олардың тұтқырлығы (вязкость) деп атайды.

Мысалы сұйықтың екі қабатының арасы х метр болсын. Бірінші қабаттағы сұйық бөлшектері υ₁ - жылдамдықпен, ал екінші қабаттағысы υ₂ - жылдамдықпен қозғалсын.

Демек, бірінші қабаттан екінші қабатқа өту барысында, сұйық ағысы, әрбір метр үшін мына шамаға өзгереді:

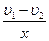
Әрбір қабатты белгілі аудан беті бар болғандықтан, осы екі қабат арасындағы үйкеліс күші де аудан шамасына қарайлас болады, яғни:

F~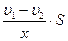

Теңдеудің сол жағында үйкеліс күші, ал оң жағында сұйық бөлшектерінің бірлік қашықтықтағы жылдамдық өзгерісі мен оның аудан беті. Міне осы шамаларды өзара теңестіру үшін пропорционалдық коэффициент кіргіземіз және оны тұтқырлық коэффициенті деп атаймыз.

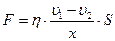
Тұтқырлық коэффициентінің мазмұнын ашу үшін теңдікті төмендегіше жазалық:

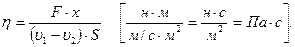
Егер, S = 1 және (υ₁ – υ₂)/х =1 болса, онда F = η.

Демек аудан бетерінің шамалары бірге тең, өзара сұйық қабаттарының ағу жылдамдығының өзгерісі бірге теңелгенде – үйкелі күші – тұтқырлықты сипаттайтын болғаны. Тұтқырлық бірлігіне н∙с/м² немесе Па∙с қабылданады.

Көп ерітінділердің тұтқырлығын су тұтқырлығымен салыстыра отырып анықтайды. Бұл шама салыстырмалы тұтқырлық (η_с) деп аталады.

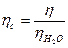
Салыстырмалы тұтқырлық – ерітінді тұтқырлығының судан тұтқырлығы неше есе басым екендігін білдіретін шама.

Сонымен қатар,меншікті тұтқырлық –η_м – ұғымы да қолданылады

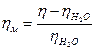
Меншікті тұтқырлық ерітілетін затты еріткішке қосу барысында тұтқырлықтың артуын сипаттайды.

Коллоидты ерітінділер үшін олардың бөлшектері шар тәріздес болып келсе, онда салыстырмалы тұтқырлық Эйнштейн теңдеуімен беріледі:

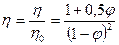
Мұндағы φ – коллоидты ерітінді бойындағы дисперстік фазаның көлемдік үлесі.

Өте сұйытылған коллоидты ертінділер үшін жоғарыдағы теңдік мына түрінде жазылады:

η_с=1+2,5φ немесе η=η₀(1+2,5 φ)

Сырттан күшпен әсер етіп, қысым түсіргенде тұтқырлығы өзгермей тұрақты мәнге ие болатын сұйықтар - ньютон сұйықтары деп аталады.

Ньютон сұйықтарына, көбіне, ламинарлық ағысқа ие ерітінділер жатады.

Коллоидты ерітнділердің ішінде, лиофобты зольдер түріне қарағанда, лиофильді зольдердің тұтқырлығы жоғарылау болып келеді.

Тұтқырлықты анықтаудың әртүрлі әдістері бар. Соның бірі Пуазейль ұсынған теңдеуді пайдалану, яғни:

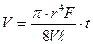
Мұндағы: V – капилляр түтікшеден ағып шығатын сұйық көлемі, м³;

r – капиллярдың радиусы, м;

F – сұйық ағуына себепкер күш, н;

t – сұйық ағып өтуіне қажетті уақыт, с;

ι – капилляр түтіктің ұзындығы, м.

Бұл теңдіктен тұтқырлық және уақыт шамасын анықтау оңай.

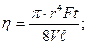
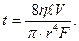
Коллоидты ерітінділер үшін көп жағдайда дисперсионды орта су болғандықтан олардың тұтқырлығын суға салыстыра отырып анықтайды.

Егер, V, r, ι шамаларын қарастырып отырған жағдайда тұрақты етіп алсақ, мынандай белгілеу енгізуімізге болады:

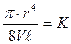
Осы жағдайды ескерек, тұтқырлықты анықтау формуласы мына түрге енеді.

η = KFt

Салыстырмалы тұтқырлық үшін мына қатынас орынды:

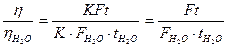
Сұйықтар өз ауырлық күші әсерінен бірдей деңгейден ағып шығатын болса, F шамасын тығыздықпен алмастыруға болады:

Демек,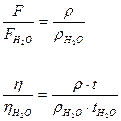

Ал бұл теңдеуден анықталуға тиісті тұтқырлық шамасы оңай есептелінеді:

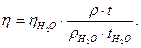
Судың тұтқырлық коэфициентін және тығыздығын бір деп алып, коллоидты ерітндінің салыстырмалы тұтқырлығын анықтау оңай:

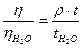
Ол үшін, капилляр түтікшеден, судың нақты бір көлемінің, онан соң анықталуға тиісті коллоидты ерітіндінің соншалықты көлемінің ағып өту уақытын анықтау қажет.

Алынған мәліметтер бойынша салыстырмалы тұтқырлықты есептеу оңай.

Жоғарыда келтірілген Ньютон – Пуазейль заңдылығына бағынбайтын сұйықтар бейньютондық сұйықтар деп аталады да ‘’ псевдопластикалы ’’және ‘’дилатантты ’’ болып екіге бөлінеді.

Псевдопластикалық сұйықтарда - әсер еткен күш шамасымен салыстырғанда сұйықтың ағыс жылдамдығы жедел артады.

Дилатантты сұйықтарда - әсер еткенкүш шамасымен салыстырғанда сұйықтың ағыс жылдамдығы баяу өзгереді.

Аталған түрдегі сұйықтармен коллоидты химияның арнаулы салалары айналысады.

Ал, коллоидты ерітінділер тұтқырлығын пайдалануда тақырыпты түсінікті меңгеру үшін мысалдар қарастыралық.

1 – мысал. Кремний диоксиді зольінің тұтқырлығы суға қарағанда 10% жоғары. Дисперсті фаза тығыздығы 2,7 г/см³, ал су үшін бұл шама 1,02 г/см³. α = 2,5 деп қабылдай отырып, зольдің массалық үлес концентрациясын анықта.

Берілгені:

η = 1,1 η₀ Эйнштейн формуласын пайдаланамыз.

α = 2,5 Есеп шарты бойынша: η = 1,1 η₀

d = 2,7 г/см³ η = η₀(1+2,5φ); 1,1 η₀= η₀(1+2,5φ)

ρ = 1,02 г/см³

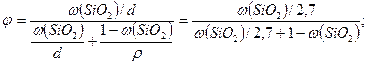
ω -?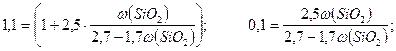

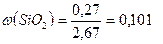немесе 10,1%

2 – мысал. Алюминий оксидінің зольі алынған. Зольдің массалық үлес концентрациясы 0,12, тұтқырлығы 1,18∙10^-3 Па∙с. Коллоидты бөлшек радиусы 10 нм. Дисперсті фаза тығыздығы 4 г/см³, ал дисперсионды ортаныкі 1 г/см³. судың тұтқырлығы 1∙10^-3 Па∙с. Бөлшектердің пішін коэффициенті – α = 0,25. коллоидты ерітінді Ньютон заңдылықтарына бағынатын болса, онда коллоидты бөлшектің сольваттық қабатының қалыңдығы қандай болады?

Талдау. Есеп бір қарағанда күрделі болғанымен байыппен қарасаңыз, онша қиындығы жоқ. Асықпай және шартын оқыңыз. өзіңізше шығарып, онан соң оқулықтағымен салыстырыңыз!

Ең бірінші кезекте ньютон сұйықтарына арналған коллоидты ерітінділер үшін Эйнштейн теңдеуін еске түсіреміз:

η = η₀(1+ αφ)

мұндағы φ – дисперсті фазаның көлемдік үлесі екендігі белгілі.

Тұтқырлықты анықтаудың бәрі де гидраттанған коллоидты бөлшектерінен жүзеге асырылғандықтан бұл жердегі φ – гидраттанған бөлшектердің көлемдік үлесі.

Ал, гидраттанған коллоидты бөлшектердің көлемдік үлесі мына формуладан анықталатынына ешкім шүбә келтірмес:

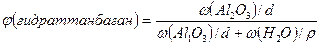
Егер, коллоидты бөлшектің радиусы r болса, гидраттанған бөлшектікін (r +δ) деп қабылдаймыз. Мұндағы δ – сольваттық қабат қалыңдығы. Коллоидты бөлшек саны n десек, онда шар тәріздес бөлшектер үшін мына теңдік орынды:

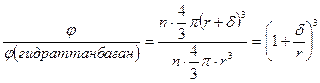
Талдау нәтижесінде есепті ауызша шығарып та қойдық.

Енді,тек берілген мәліметтерді жазып алып, есептеу қалды.

Берілгені:

ω = 0,12 бірінші кезекте Эйнштейн формуласы

η = 1,18 ∙10^-3 Па∙с формуласы бойынша гидратталған дис -

r = 10 нм =1 ∙10^{-8 м персті фазаның көлемдік үлесін анықта-}

d = 4 г/cм³ = 4 ∙10³ кг/м³ лық: η = η₀(1+ α φ) теңдігінен φ – ді

ρ_н2о = 1 г/см³ = 1 ∙10^-3 кг/м³ анықтаймыз:

α = 0,25

η_н2о = 1 ∙10^-3 Па∙с

δ -?

Осы бөлшектер гидраттанбаған жағдайдағы көлемдік үлес бөлігін есептелік:

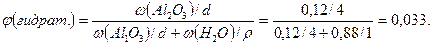
Талдау барысындағы алынған теңдікке қойып δ – шамасын анықтаймыз:

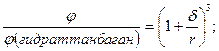
Бұл теңдіктен гидраттану қабатының қалыңдығын анықтайық

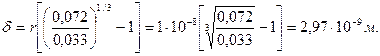
Гидраттану қабатының қалыңдығы 2,97 нм. Коллоидты бөлшек радиусы 10 нм. Демек, диаметрі 20 нм.

Гидраттанған қабатты ескерсек, мицелланың диаметрі

20 + 2,97 = 22,97 нм

Date: 2015-05-08; view: 2381; Нарушение авторских прав