
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Седиментация
|
|
Ауырлық күшінің әсерінен бөлшектердің тұнбаға түсу процесін седиментация деп атайды. Тұнбаға түсу жылдамдығы бөлшектердің көлеміне, тығыздығына, ортаға, сұйықтыққа және ауырлық күшінің уақытына тәуелді. Стокс заңы бойынша қозғалу кезінде бөлшектер сфералық тұтқыр ортада қарсылық күшін сезеді, ол тең 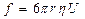
мұндағы, 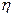 - орта тұтқырлығы,
- орта тұтқырлығы, 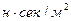 , r – бөлшек радиусы, м.
, r – бөлшек радиусы, м.
U – тұнба түсу жылдамдығы, м/сек, Басқа жақтан бөлшекке күш әсер етеді.
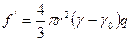
мұндағы, 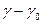 - дисперсті ортадағы бөлшектер тығыздығының айырымы, кг/м3
- дисперсті ортадағы бөлшектер тығыздығының айырымы, кг/м3
q – ауырлық күшінің жылдамдығы, м/сек2
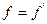 тең болғанда және тұрақты температурада тұнбаға тұрақты түсу жылдамдығына жетеді
тең болғанда және тұрақты температурада тұнбаға тұрақты түсу жылдамдығына жетеді
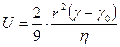
Бөлшектердің тұнбаға түсу жылдамдығын бөліп алып, оның радиусын есептейміз.
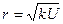
мұндағы, 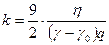 берілген суспензияға тұрақты шама.
берілген суспензияға тұрақты шама.
Тұнбаға түсу жылдамдығы бөлшек радиусына тәуелді. Мысалы, саз бөлшегінің 1∙10-5 м радиусты 1см-ге 43сек.уақыт өтеді, ал 2∙10-6 м радиуста 17 минут, 1∙10-8м радиуста – 500 күн кетеді. Егер бөлшек 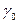 тығыздықта қозғалатын болса, онда оның қозғалысы төменнен жоғарыға, ал зат бөлшегінің тығыздығы
тығыздықта қозғалатын болса, онда оның қозғалысы төменнен жоғарыға, ал зат бөлшегінің тығыздығы 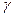 немесе орта тығыздығына
немесе орта тығыздығына 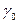 тәуелді болады.
тәуелді болады.
Суспензияда 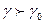 және бөлшектер тұнбаға түседі, эмульсияда
және бөлшектер тұнбаға түседі, эмульсияда  сондықтан бөлшектер қалқып шығады. Мысалы, судағы саздың тұнуы, сүттегі қаймақтың түзілуі жатады.
сондықтан бөлшектер қалқып шығады. Мысалы, судағы саздың тұнуы, сүттегі қаймақтың түзілуі жатады.
Бөлшектердің толық түсуі ауырлық күшінің әсерінен болмайды, өйткені оған қарсы броундық қозғалыс әрекет етеді, яғни ол бөлшектерді ерітіндінің барлық көлеміне тең бөлуге тырысады. Броун қозғалысының әсері көп әсер етеді, егер бөлшектің көлемі кішкентай болған жағдайда.
Егер бөлшектердің негізгі бөлігі қысқа мерзімде тұнса, онда ондай жүйені кинетикалық тұрақсыз деп атайды, ал егер бөлшектер ұзақ мерзім ішінде тепе-тең бөлінсе, оны кинетикалық тұрақты жүйе деп атайды.
Суспензия мен эмульсиялар – бұлар кинетикалық тұрақсыз жүйе, ал коллоидты жүйе мен ерітін ділер жоғарғы молекулярлы – кинетикалық тұрақты.
Седиментация процесі кинетикалық тұрақсыз жүйе – суспензияға тән.
Кинетикалық тұрақты тұнуды қарапайым жағдайда түзуге болады, егер жердің ауырлық күшінің центрге тартқыш күші жоғары болса. Центрифуга арқылы центрге тартқыш күшті алуға болады, 105 есе артық ауырлық күші бар және бөлшектің тұну жылдамдығын сонша есе жылдамдатуға болады. Центрифугат қолдану арқылы коллоид пен жоғарғы молекулярлы ерітінділерге седиментация жүргізуге болады.
Седиментациялық анализ тұнған бөлшектердің жылдамдығын өлшеуге негізделген. Тәжірибеде кездесетін суспензия қарапайым полидисперсті, онда әртүрлі көлемдегі бөлшектер болады. Седиментация процесі өндірісте қолданылады. Тұну жылдамдығын бақылау бөлшектердің салмақтық, сандық анықтауға әртүрлі көлемдегі полидисперсті жүйедегі мүмкіндік береді. Бұл принципке сүт сепараторының жұмысы негізделген, яғни сүттен қаймақты айыру процесі. Сепарация процесі (айыру) центрлік тартқыш күш арқылы тез өтеді, сүттің сол қалпында тұрғанына қарағанда.
Седиментацияны қолдану центрге тартқыш өріс арқылы жоғарғы молекулярлы ерітінділердегі бөлшектердің көлемін анықтайды.
Сұйық не газды ортадағы ұнтақталған заттың бөлшектері қарама-қарсы бағытталған екі күштің әсерінде болады. Олардың біріншісі бөлшекті төмен тартып, тұнбаға немесе шөгіндіге түсіруге бағытталған ауырлық күш, ал келесі бөлшектерді берілген көлемде біркелкі таратуға ұмтылған, яғни бөлшек концентрациясы мол жақтан, аз жаққа қарай ауысуына әсер ететін өздігінен жүретін диффузиялық күш. Дисперстік системаға әсер ететін ауырлық және диффузиялық күштің қайсысының басым болуына байланысты оның күші анықталады: ауырлық күші артық болса, ондайда дисперсті системаның бөлшектері көбірек шөгеді, ал диффузиялық күш басым болса, онда дисперстік системадағы бөлшектер тұнбаға түспей жүзгін түрінде болады. Осы айтылғандарға орай, дисперсті фазаның система көлемінде біркелкі таралып, тұрақты күйде болуын седиментациялық немесе кинетикалық тұрақтылық деп атайды, ал ауырлық күші әсерінен бөлшектердің тұнбаға түсу процесі седиментация деп аталады. Системадағы бөлшектердің тұнбаға түсу жылдамдығы осы бөлшектердің өлшеміне, дисперстік ортаның тұтқырлығына және бөлшек тығыздықтарына тәуелді:
υ= 2/3 · r2 (d-d) g / η (42)
мұндағы υ- бөлшектердің тұнбаға түсу жылдамдығы; r- бөлшек радиусы; d және d0- дисперсті бөлшек пен дисперстік ортаның тығыздықтары; η- дисперстік ортаның тұтқырлығы; g- еркін түсу үдеуі.
Дисперсті фаза өте ұсақ болса диффузия жылдамдығы үлкен болады. Ал олар іріленген сайын диффузия жылдамдығы баяулайды. Бөлшектің радиусы 2 нм-ден үлкен болса, броундық қозғалыс байқалмайды, демек олардың диффузиялық қабілеті нөлге тең. Мұнда ауырлық күші диффузиялық күштен басым.
Егер дисперсті системадағы ауырлық күші мен диффузия күші өзара тең болса, онда седиментация мен диффузия жылдамдықтарының тепе-теңдігімен сипатталатын седиментациялық тепе-теңдік деп аталатын күй орнайды. Мұндайда берілген дисперсті системаның бірлік өлшемі арқылы ауырлық күшінің әсерінен төменқарай қанша бөлшек өтсе, диффузиялық күш ықпалынан жоғарыға қарай сонша бөлшек өтеді. Осындай седиментациялық тепе-теңдік коллоидты системаға ғана емес, молекулалық-дисперстік системалар үшін де тән құбылыс. Сондай-ақ бұл тепе-теңдік системадағы бөлшек концентрацияларының уақыт өткен сайын баяу болса да төменнен жоғарыға қарай кеми беретіндігімен де сипатталады. Сұйық бағанасындағы бөлшектер өзінің өлшеміне сәйкес әртүрлі биіктікте, айталық ірілері төмен, ал ұсақтары жоғары орналасады екен. Бұл құбылысты сипаттау үшін Лапластың гипсометриялық немесе барометрлік заңын коллоидты системаға пайдалануға болады: золь бағанасының биіктігін арифметикалық прогрессияда көбейткенде, бөлшек концентрациясы геометриялық прогрессияда кемиді. Бұл заңдылықты математикалық тұрғыдан өрнектесек:
h = RT ln C1/С2 / M·g (43)
мұндағы C1 – берілген биіктіктегі дисперсті системаның концентрациясы; С2 – осы системаның h биіктіктегі концентрациясы; h- өлшентін бағ- өлшентін бағана биіктігі; М- заттың салщыстырмалы молекулалық массасы; g- еркін түсу үдеуі.
4- кестеде әртүрлі дисперсті дәрежеде ұсақталған кейбір дисперсті системалардың мәліметтері келтірілген.
Әуелде Лапластың гипсометриялық заңы газ тәрізді және молекулалық-дисперстік системаларға арналып тұжырымдалған болатын. Бертін келе Перрен оны коллоидтық-дисперстік, тіпті ірі дисперстік системаларға қолданды. Осы мақсатпен Перрен радиустері әртүрлі көптеген шариктер әзірлеп, оларды өлшеміне орай сұрыптап, дисперстік ортаны да белгілі сипатта даярлап, көптеген тәжірибелер жүргізді. Олардың нәтижесі Лаплас заңына қайшы келмеді. Сонымен, ол әртүрлі биіктіктегі бөлшектердің санын анықтай келіп, Авогадро санының мәнін асқан дәлдікпен табуға болатынын көрсетті.
Перрен өз тәжірибелерінің нәтижесінде басқа да әдістер мен теңдеулер көмегімен анықталған Авогадро санының мәнінен алшақ емес, қанағаттанарлықтай дерек алды. Олай болса Перрен еңбектеріндегі зерттеулер тек молекулалық-кинетикалық теорияның дұрыстығын дәлелдеп қана қоймай, оны коллоидтық-дисперстік системаларға да қолдануға болатынын бұлжытпай, ешбір шүбәсіз дәлелдеп берді.
4-кесте 5-кесте
| Белокты зат | Бөлінді масса |
| Пепсин | 39 200 |
| Жұмыртқадағы Альбумин | 43 500 |
| Гемоглобин | 68 100 |
| Фитоциан | 279 000 |
| Октопус-гемо- цианин | 2 785 000 |
| Ұнтақталған Зат | Бөлшек диаметрі, нм | Бөлінді кон- центрация екі есе кемитін биіктік, м |
| Оттек Жоғары дисперсті алтын | 0,27 1,85 | 2,15 |
| Орташа дисперсті алтын | 8,35 | 0,025 |
| Ірі дисперсті алтын | 186,0 | 2,10-7 |
Седиментациялық талдау әдістерінің бәрі де дисперстік фазадағы бөлшектердің тұнбаға шөгу жылдамдығын анықтауға негізделеді. Тәжірибе кезінде анықталған бөлшектердің шөгу жылдамдығын пайдаланып, олардың басқа да өлшемдерін (дисперстік дәрежесін, бөлшек радиусын, бағана биіктігін және т.б.) табуға болады. Мысалы, дисперстік системадағы бөлшектердің радиусын табу үшін жоғарыдағы (42) теңдеуді ықшамдап жазуға болады:
r = 6,78·10-2 √Vn /(d-d0) (44)
Коллоидты системадағы бөлшектердің дисперстік дәрежесі өте жоғары болғандықтан, ондағы бөлшектердің тұнбаға шөгу жылдамдығы баяу. Ал кейде оны жылдамдату мақсатымен ультрацентрифуга аспабын пайдаланады. Осындай аспаптарының көмегімен көптеген белоктың, күрделі және жоғары молекулалық қосылыстардың массалары анықталды. Оның кейбір жекеленген мысалдары 5-кестеде келтірілген.
Ауырлық күшінің әсерінен коллоидты бөлшектердің ерітінді түбіне шөгуін седиментация деп атайды.
Ерітінді бойындағы бөлшектің қозғалысына сұйықтың қарсы әсер етуші күші бөлшек радиусымен орта тұтқырлығына қарайлас екендігі белгілі, яғни:
F = 6πηυr
Мұндағы υ - бөлшектердің қозғалыс жылдамдығы.
Ал коллоидты бөлшектердің ауырлық күші бөлшек радиусымен еріткіш тығыздығына тәуелді болатындығы мына теңдеумен сипатталады:
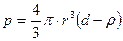 g.
g.
Мұндағы. d – коллоидты бөлшектердің тығыздығы;
g – еркін түсу үдеуі;
ρ – орта тығыздығы.
Коллоидты ерітінді бойында тепе – теңдік сақталуы үшін р = F болуы шарт, яғни: 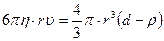 g
g
Бұл теңдіктен бөлшектердің қозғалыс жылдамдығын анықталық:
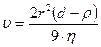 g
g
Теңдіктен мынадай тұжырымдар туындайды:
1. (d - ρ) < 0. Онда υ < 0. демек, ерітінді бойындағы бөлшектер оның бетіне жиналуға ұмтылады.
2. (d - ρ) > 0, υ > 0. Бұл ерітінді бойында коллоидты бөлшектер шөгуге ұмтылады.
Келтірілген теңдіктер Стокс заңдылығының мазмұнын ашады. Коллоидты бөлшектердің жүзінділердің тұнбаға шөгу жылдамдығын талдай отырып, олардың радиусын анықтау седиментациялық анализ немесе седиментациялық талдау деп аталады.
Жоғарыда келтірілген теңдіктен r шамасын анықтайды:
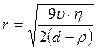
Мұндағы 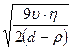 мүшелігінде шамалар мәні қарастырылып отырған жағдай үшін тұрақты болғандықтан, оны К деп белгілеп теңдікті төмендегіше жазуға болады.
мүшелігінде шамалар мәні қарастырылып отырған жағдай үшін тұрақты болғандықтан, оны К деп белгілеп теңдікті төмендегіше жазуға болады.

Коллоидты бөлшектер жүзінділердің седиментацияға бейімділігін бөлшектердің қозғалыс жылдамдығын еркін түсу үдуіне қатынасымен сипаттайды да Sсед таңбасымен белгілеп, седиментациялау константасы деп атайды.
Седиментациялау константасының бірлігіне сведберг немесе секунд қабылданады. Бір сведберг (сб) 10-13 с тең.
Седиментация константасынаң кері шамасы дисперсті жүйенің кинетикалық тұрақтылығын анықтайды:
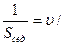 g
g
Кинетикалық тұрақтылыққа ие дисперсті жүйелердегі коллоидты бөлшектердің шөгуін центрден тепкіш күш әсерін пайдаланып “центрифуга” деген құралдарда тұнбаға көшіруге болады. Мұндай әдісті алғаш болып жүзеге асырған ғалымдар А.В.Думанский және Т.Сведберг.
Центрифуганың арнаулы ұяшықтарына пробиркадағы коллоидты ерітінділер орналастырылады. Бұл ыдыс беті жабылып, сыртқы энергия көзінен қатты айналдырылады. Еркін түсу үдеуі g центрден тепкіш күш үдеу - ω2h – шамасымен алмастырылады. Мұндағы ω – бұрыштық айналу жылдамдығы. h – ротордан бөлшектерге дейінгі аралықты көрсетеді.
υ - центрифуга үшін dh/dt - шамасымен алмастырылады.
Коллоидты бөлшектердің центрден тепкіш күш әсерінен тұнбаға шөгу жылдамдығы мына теңдікпен өрнектеледі:
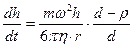
Шар тәріздес бөлшектер масасын олардың радиусы арқылы сипаттасақ теңдік мына түрге енеді:
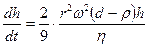
Айнымалыларды айырып, дифференциалдық теңдеуді шешсек нақты t - уақыт бөлігі үшін коллоидты бөлшектерлің h1 - деңгейінен h2 - деңгейіне шөккені үшін шешімі төмендегідей болады:
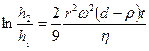
Бұл формуладан коллоидты бөлшек радуысын оңай анықтайға болады:
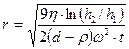
Бұл теңдеу Тальбо – Сведберг теңдеуі деп аталады.
Айтқанымыз түсінікті болу үшін мысалдар қарастыралық.
1 – мысал. Коллоидты бөлшектердің радиусы 1∙10-1 м–ге тең золь берілген. Осы зольдің ауырлық күші әсерінен және центрден тепкіш күш әсерінен орын алатын седиментациялау жылдамдығын есептеп, өзара салыстырыңыз. Дисперсті фаза тығыздығы 2∙10-3 кг/м3, ал дисперсионды орта тығыздығы 1∙10-3 кг/м3. орта тұтқырлығы η = 1∙10-3 Па∙с. Центрден тепкіш күш үдеуі ω2h = 200g.
Шешімі: Ауырлық күші әсерінен (жердің тарту күші – гравитациялық өріс) орын алатын коллоидты бөлшектердің шөгу жылдамдығы 4.12 формула бойынша есептеледі, яғни:
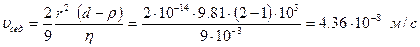
Центрифугада орын алатын седиментациялау жылдамдығын 4.39 формуласы бойынша есептейміз.
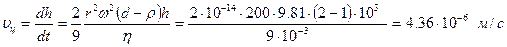
Екі жылдамдықты өзара салыстыралық.
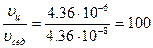
Демек, центрифугада коллоидты бөлшектердің тұнбаға шөгуі жүз есе жылдам орын алатын болғаны.
2 – мысал. Тығыздығы 3∙103 кг/м3 тең зат, радиусы 5∙10-8 м-ге дейін ұнтақталды. Тығыздығы 1∙103 кг/м3 болатын ортада коллоидты ерітінді алынды. 300К – де орта тұтқырлығы 1∙10-3 Па∙с. Коллоидты бөлшектерді тұндыру үшін центрден тепкіш үдеудің шамасы қандай болуы тиіс?
Талдау. Коллоиды бөлшектер тұнбаға көшу үшін, олардың броундық қозғалысынан тұнбаға шөгу жылдамдығы басым болуы шарт. Броундық қозғалыс нәтижесінде бөлшек жылдамдығын сипаттау үшін, коллоидты бөлшектердің орташа ауытқу шамасы бар екендігі белгілі, яғни:

Ал, центрифугада центрден тепкіш күш әсерінен бөлшектердің тұнбаға шөгу жылдамдығы шамасынан он еседей жылдам болуы керек.
Центрден тепкіш күш әсерінен бөлшектердің седиментациялау жылдамдығы мына формуламен есептелінетіні белгілі:
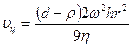
Енді есептің берілгендерін жазып алып, шығаруға кіріселік.
Берілгені:
ρ = 1∙103 кг/м3 Бірінші кезекте орташа ауытқу шамасын
η = 1∙10-3 Па∙с есептелік:
T = 300K
r = 5∙10-8 м 
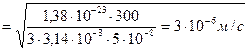
d = 3∙103 кг/м3
ω2h -?
Центрден тепкіш күш әсерінен бөлшектер тұнбаға көшу үшін, тұнбаға шөгу жылдамдығы (υ) 3∙10-6 м/с шамасынан он еседей жылдам, яғни 3∙10-5 м/с болуы шарт. Осы шартты қабылдай отырып, центрден тепкішүдеу шамасын ω2h – есептелік:
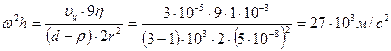
немесе
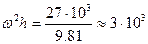 g.
g.
3 – мысал. Тығыздығы 3∙103 кг/м3зат, радиусы 10-7м болатындай етіліп, тығыздығы 1∙103 кг/м3 болатын ортада ұнтақталды. Орта тұтқырлығы 1∙10-3 Па∙с. Ыдыстағы коллоидты ерітіндінің биіктігі 0,1 м. Центрден тепкіш үдеу шамасы ω2h = 200g. Коллоидты бөлшектер центрифугада қанша уақытта тұнбаға шөгеді? Ал ауырлық күшінің әсерінен ше? Екі жағдайды салыстырыңыз.
Талдау. Талдау барысында не берілгендігі, есеп нені сұрап отырғандығына баса назар аударылады. Келтірілген есепті өзіңізде де біліп отырсыз! Ауырлық күші әсерінен тұнбаға шөгу жылдамдығын және центрден тепкіш күш әсерінен шөгу жылдамдығын анықтасақ, онда биіктікті жылдамдыққа бөлу арқылы уақыт оңай анықталады, яғни:
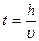
Мұндағы h - биіктік коллоидты бөлшектердің жүретін жолы.
Бұл жерде екі жағдай үшін υ - мәні екітүрлі.
Олай болса, жылдамдықтарды анықтап есепті шешу ғана қалды. Берілгендерді жазып алып, есептеуге кіріселік.
Берілгені: Шешуі:
ρ = 1∙103 кг/м3 Ауырлық күші, гравитация әсерінен тұнбаға көшу
η = 1∙10-3 Па∙с жылдамдығын есептейміз:
r = 10-7 м
d = 3∙103 кг/м3 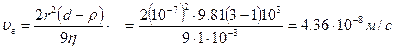
h = 0,1 м
ω2h = 200g
tr,tц -?
Центрден тепкіш күш әсерінен тұнбаға көшу жылдамдығын (υц) есептейміз:
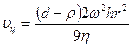 =
= 
Ауырлық күші әсерінен тұнбаға көшуге кететін уақыт бөлігі - tr:
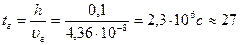 сөтке.
сөтке.
Центрден тепкіш күш әсерінен центрифугада тұнбаға көшуге кететін уақыт бөлігі - tц:
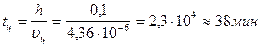
Демек, центрифуга көмегімен коллоидты ерітінділерді жылдам тұнбаға көшіруге болады.
4 – мысал. Хлорлы күміс зольін центрифуганы пайдаланып тұнбаға көшірді. Центрифугалау барысында 0 мин ішінде бастапқы 0,09 м болатын деңгей 0,14 м – ге жетті. Дисперсті фаза тығыздығы d =5,6∙103 кг/м3. дисперсионды орта тығыздығы 1∙103 кг/м3, ал тұтқырлығы 1∙10-3 Па∙с. Центрифуганың айналыс жиілігі минутына мың айналым.
Коллоидтық бөлшек радиусын есепте.
Талдау. Коллоидты бөлшек формасын шар тәріздес деп қабылдасақ, оның радиусын есептейтін формуланы білеміз.
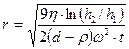
Формулада бұрыштық жылдамдық бар, ал есеп шартында центрифуганың айналыс жиілігі берілген. Бұрыштық жылдамдықпен айналыс жиілігі арасындағы формуланы еске түсіреміз:
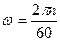 .
.
Мұндағы n – айналыс жиілігі, 1 мин – 60 секунда бар.
Есепті шығаруға мәліметтерді жазып аламыз.
Берілгені: Есептеу:
ρ = 1∙103 кг/м3 Коллоидты бөлшек радиусын есептеу
η = 1∙10-3 Па∙с үшін бұрыштық жылдамдықты анық -
d = 5,6∙103 кг/м3 тап аламыз:
h1 = 0,14 м
h2 = 0,09 м 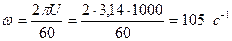 .
.
t = 10 мин
U = 1000 айн/мин Енді радиусты есептейміз:
r -? 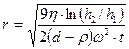
Колллоидты химия саласының седиментациялық талдау деген үлкен саласы бар. Седиментациялық талдаудың интегралды және дифференциалды қисық сызықтарын тұрғызу, коллоидты бөлшек радиустарын анықтауда әртүрлі әдістермен қатар номограммаларды есеп шығаруда пайдалану мына оқулықта жақсы берілген.
Расчеты и задачи по коллоидной химии. Под ред. В.И.Барановой. М. Высш. шк., 1989. – С. 88 – 121.
5 – мысал. Ауырлық күшінің әсерінен тығыздығы 2,1 г/см3, дисперстілігі 0,8 мкм-1 болатын коллоидты бөлшектер, 0,1 м биіктіктегі ерітіндіден қанша уақыт ішінде тұнбаға шөгеді. Орта тұтқырлығы 2∙10-3 Па∙с, тығыздығы 1,1 г/см3. осы коллоидты бөлшектер центрден тепкіш күш әсерінен қанша уақыт ішінде тұнбаға көшеді? Центрифуганың айналу жылдамдығы секундына 600 айналым, ал h0 = 0,15 м.
Талдау. Стокс заңы бойынша радиусы r – ге тең бөлшектердің тұнбаға шөгу жылдамдығы төмендегі формуламен анықталады:
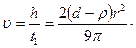 g
g
Бұл теңдіктен тұнбаға шөгу уақыты t мынаған теңеледі:
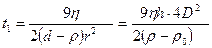
Мұндағы D – дисперстілік 1/2r шамасына тең.
Ал центрифуганы пайдаланатын болсақ, онда олардың өзіндік есептеу формуласы бар, яғни:
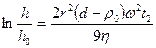
Мұндағы h = h0 + h1= 0,15 + 0,10 = 0,25 м және ω = 2πn екендігін есте ұстауымыз қажет. Бұл формуладан да t – оңай есептелінеді. Ендеше есептеуге кіріселік:
Берілгені:
D = 0,8 мкм-1 = 8∙10-5м 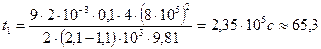 сағат.
сағат.
ρ = 1,1 г/см3 Центрифугадағы шөгу уақыты:
η = 2∙10-3 Па∙с
d = 2,1 г/см3 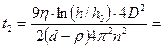
h=0,1м 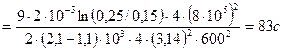
h0 = 0,15
n = 600 айн/с
t1, t2 -?
Ауырлық күшімен шөгуге кететін уақыт шамасы 65,3 сағат. Центрифугамен шөгуге қажетті уақыт шамасы – 83 с ≈ 1,4 мин.
Date: 2015-05-08; view: 4544; Нарушение авторских прав