Дебаевская длина экранирования

Количественной характеристикой эффекта поля, характеризующей глубину проникновения поля в полупроводник, является дебаевская длина экранирования. Рассмотрим случай, когда полупроводник внесен во внешнее слабое поле. Критерий слабого поля заключается в том, что возмущение потенциальной энергии невелико по сравнению с тепловой энергией, то есть величина поверхностного потенциала y _s будет меньше kT / q. Воспользуемся для нахождения распределения электростатического потенциала y _s в ОПЗ уравнением Пуассона, при этом будем считать, что ось z направлена перпендикулярно поверхности полупроводника:

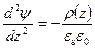, (2.18)

где r (z) – плотность заряда в ОПЗ,

e _s – относительная диэлектрическая проницаемость полупроводника.

Заряд в ОПЗ состоит из заряда ионизованных доноров и заряда свободных электронов:

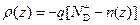. (2.19)

Величина N _D⁺ = n _0, а n (z) описывается соотношением (2.16). Поскольку в нашем случае by _s << 1, то

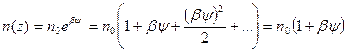. (2.20)

Тогда плотность объемного заряда

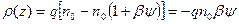. (2.21)

Подставляя значение r (z) из (2.22) в (2.18), получаем:

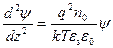. (2.22)

Введем характерную величину

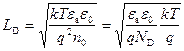(2.23)

и назовем ее дебаевской длиной экранирования.

Тогда уравнение (2.22) придет к виду:

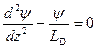. (2.24)

Решение дифференциального уравнения (2.24) имеет вид:

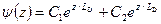. (2.25)

Используем граничные условия:

при 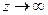, 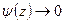получаем C ₁ = 0,

при z = 0, y (z) = y _s получаем С ₂ = y _s

Таким образом, при малом возмущении электростатический потенциал, а следовательно, и электрическое поле спадают по экспоненциальному закону вглубь полупроводника:

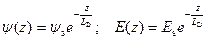. (2.26)

Известно, что если произвольная величина f (z) описывается законом

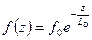, (2.27)

то среднее значение z, определяющее центроид функции f (z), равно:

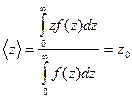. (2.28)

Таким образом, по физическому смыслу дебаевская длина экранирования L _D соответствует среднему расстоянию, на которое проникает электрическое поле в полупроводник при малых уровнях возмущения.

2.6. Контакт металл – полупроводник. Барьер Шоттки

Рассмотрим контакт металл – полупроводник. В случае контакта возможны различные комбинации (p‑ и n ‑типы полупроводника) и соотношения термодинамических работ выхода из металла и полупроводника. В зависимости от этих соотношений в области контакта могут реализоваться три состояния. Первое состояние соответствует условию плоских зон в полупроводнике, в этом случае реализуется нейтральный контакт. Второе состояние соответствует условию обогащения приповерхностной области полупроводника (дырками в p ‑типе и электронами в n ‑типе), в этом случае реализуется омический контакт. И, наконец, в третьем состоянии приповерхностная область полупроводника обеднена основными носителями, в этом случае в области контакта со стороны полупроводника формируется область пространственного заряда ионизованных доноров или акцепторов и реализуется блокирующий контакт, или барьер Шоттки [15, 16].

В полупроводниковых приборах наибольшее применение получили блокирующие контакты металл – полупроводник, или барьеры Шоттки. Рассмотрим условие возникновения барьера Шоттки. Ранее было показано, что ток термоэлектронной эмиссии с поверхности любого твердого тела определяется уравнением Ричардсона:

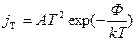. (2.29)

Для контакта металл – полупроводник n ‑типа выберем условие, чтобы термодинамическая работа выхода из полупроводника Ф _п/п была меньше, чем термодинамическая работа выхода из металла Ф _Ме. В этом случае согласно уравнению (2.29) ток термоэлектронной эмиссии с поверхности полупроводника j _п/п будет больше, чем ток термоэлектронной эмиссии с поверхности металла:

.

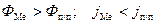При контакте таких материалов в начальный момент времени ток из полупроводника в металл будет превышать обратный ток из металла в полупроводник и в приповерхностных областях полупроводника и металла будут накапливаться объемные заряды – отрицательные в металле и положительные в полупроводнике. В области контакта возникнет электрическое поле, в результате чего произойдет изгиб энергетических зон. Вследствие эффекта поля термодинамическая работа выхода на поверхности полупроводника возрастет. Этот процесс будет проходить до тех пор, пока в области контакта не выравняются токи термоэлектронной эмиссии и соответственно значения термодинамических работ выхода на поверхности.

На рисунке 2.4 показаны зонные диаграммы различных этапов формирования контакта металл – полупроводник. В условиях равновесия в области контакта токи термоэлектронной эмиссии выравнялись, вследствие эффекта поля возник потенциальный барьер, высота которого равна разности термодинамических работ выхода: j _к = Ф _Ме – Ф _п/п.

Для контакта металл – полупроводник p -типа выберем условие, чтобы термодинамическая работа выхода из полупроводника Ф _п/п была больше, чем термодинамическая работа выхода из металла Ф _Ме. В этом случае ток термоэлектронной эмиссии с поверхности полупроводника j _п/п будет меньше, чем ток термоэлектронной эмиссии с поверхности металла, согласно уравнению (2.29).

При контакте таких материалов в начальный момент времени ток из металла в полупроводник p ‑типа будет превышать обратный ток из полупроводника в металл и в приповерхностных областях полупроводника и металла будут накапливаться объемные заряды – положительные в металле и отрицательные в полупроводнике.

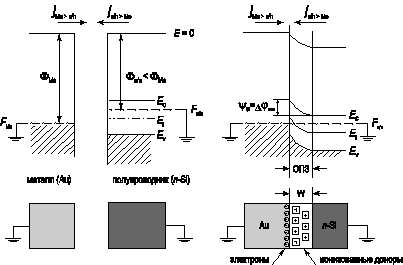
Рис. 2.4. Зонная диаграмма, иллюстрирующая образование барьера Шоттки

В дальнейшем картина перехода к равновесному состоянию и формирования потенциального барьера для контакта металл – полупроводник p ‑типа аналогична рассмотренной выше для контакта металл – полупроводник n ‑типа.

Date: 2015-05-05; view: 970; Нарушение авторских прав