Теплопередача при внешнем обтекании тел

Интегральные уравнения теплового и динамического пограничных слоев при безнапорном обтекании пластины.
Рассмотрим участок плоской поверхности, с температурой t_w и омывается потоком несжимаемой жид-ти с темп. t_f. Ширина поверхности равна 1. на расстоянии х от начала координат выделим элемент теплового пограничного слоя ABCD длиной dx (две боковые поверхности элемента образованы вертикальными плоскостями, нормальными к оси х). Тепловой баланс этого элемента при стационарных условиях теплообмена и отсутствии в жидкости внутренних источников теплоты: Q_x – Q_x+dx+dQ’_x= dQ’’_x. Два первых члена определяют изменение энтальпии теплоносителя при течении его между поверх-ми АВ и CD, третий - подвод теплоты вместе с теплоносителем, поступивший через поверх-ть ВС. Правая часть уравнения отражает теплообмен между поверхностью и теплоносителем.
Величину Q_x+dx найдем разложением Q_x в ряд Тейлора: Q_x+dx= Q_x+(d Q_x/dx)dxПренебрегая распространением теплоты вдоль оси х найдем: Q_x= 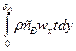где wx – переменная по толщине пограничного слоя скорость потока.dQ’_x=с_pt_fdG’_x, G’_x – массовый расход вещества через поверхность ВС. dQ’_x= 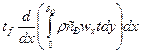теплота, проходящая через поверхность теплообмена: dQ’’_x=qdx.Подставим все выражения в первую формулу: 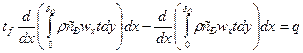Считая, что теплофизические характеристики теплоносителя от температуры не зависят, выражение примет вид: 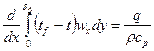. Подставив в это выражение тепловую нагрузку из уравнения Фурье, в котором температурный градиент взят по абсолютной величине, получим:
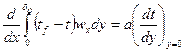Это уравнение называется интегральным уравнением для теплового пограничного слоя. Аналогично выводится уравнение для динамического пограничного слоя, (интегральное соотношением количества движения): ,

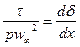где t – напряжение трения на поверхности теплообмена, δ - толщина потери импульса.

Теплоотдача пластины при ламинарном пограничном слое. Решение на основе теории динамического погр. слоя.
Зададим форму профиля скоростей в пограничном слое степенным многочленом:
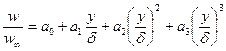Для оценки коэффициентов используем граничные условия: при у=0, w=0 и 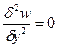; при у=δ, 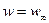и 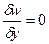. Подставив в формулу получим а0=0, а1=3/2, а2=0, а3=-1/2
Следовательно, многочлен перепишется так:

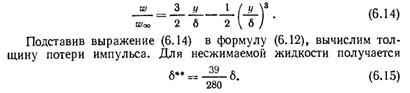(звездочки писать не надо)

Теплоотдача при внешнем обтекании труб.

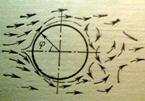
Течение при обтекании поперечной трубы.
На фронтовой части трубы образуется пограничный слой, толщина которого достигается наибольшей величины вблизи ϕ=90˚. В этой зоне происходит отрыв потока от поверхности и кормовая часть трубы омывается сильно завихренным потоком с обратными
циркуляционными токами. Показана типичная
зависимость отношения местного коэффициента
теплоотдачи αф к среднему его значению для всей трубы от угла, который определяет местоположение точки на окружности. Теплоотдача протекает наиболее интенсивно вблизи лобовой образующей цилиндра. В местах, где ламинарный пограничный слой достигает наибольшей толщины, коэффициент теплоотдачи имеет минимальное значение. Средняя теплоотдача трубы определяется уравнением, полученным экспериментальным путем: (1) 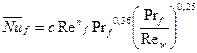в котором при Re_f 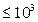c=0,56 и n=0,5, а при Re_f 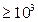c=0,28 и n=0,6. За определяющий размер в этом уравнении принят диаметр трубы, а критерий Re вычисляется по скорости невозмущенного потока. Если направление движения потока составляет с осью трубы угол отличный от 90°, то коэффициент теплоотдачи, определенный по формуле, надо умножить на поправку ε_ψ числовое значение которой приводится в справочниках. При ψ<90 то εψ<1. Теплоотдача труб, составляющих трубный пучок, зависит от расположения труб в пучке, а также от номера ряда, в котором труба находится. Характер движения теплоносителя а- коридорный, б – шахматный.
При шахматном расположении труб теплоноситель перемешивается лучше, и теплообмен протекает более интенсивно. Первый ряд труб омывается невозмущенным потоком жидкости и потому этот ряд имеет наименьший коэффициент теплоотдачи. В последующих рядах труб теплоотдача протекает более интенсивно, можно считать, что третий и последующие ряды труб имеют одинаковый средний коэффициент теплоотдачи. Если в качестве определяющего размера выбрать диаметр трубы, а критерий Re подсчитывать по скорости в наиболее узком сечении пучка (в сечении, где расположены трубы), то независимо от расстояния между трубами коэффициент теплоотдачи третьего и последующего рядов труб можно определять по уравнению (1). Числовые значения коэффициентов с и n зависят от вида пучка. При Ref << 10³ для обоих видов пучков труб
с = 0,56, n= 0,5. При Ref > > 10³ для коридорного пучка с = 0,22, n = 0,65, для шахматного с = 0,4, n = 0,6.
Коэффициенты теплоотдачи первого и второго рядов подсчитываются через коэффициент теплоотдачи третьего ряда. Для коридорного расположения труб: а1 = 0,6а3; а2 = 0.9а3; Для шахматного расположения труб: а1 = 0,6а3; а2 = 0,7а3. Когда направление скорости потока составляет с осью труб угол ψ < 90°, рассчитанный по формуле коэффициент теплоотдачи надо скорректировать поправкой εψ. Закономерности теплоотдачи зависят от формы сечения поперечно обтекаемого тела и от ориентировки тела по отношению к набегающему потоку. Уравнения подобия для тел с различной формой поперечного сечения приводятся в справочной литературе.

Date: 2015-05-05; view: 1435; Нарушение авторских прав