Диф.уравнение теплопроводности. Коэффициент температуропроводности.Уравнение Пуассона,уравнение Лапласа

-При выводе дифференциального уравнения теплопроводности принимаются следующие допущения:внутренние источники теплоты отсутствуют,тело однородно и изотропно, используется закон сохранения энергии,который для данного случая формулируется как»разность между количеством теплоты,вошедшей вследствие теплопроводности в элементарный паралепипед за время dt и вышедший из него за тоже время,расходуется на изменение внутренней энергии рассматриваемого элементарного объема.После преобразований получаем это уравнение -называется дифференциальным уравнением теплопроводности или уравнением Фурье и лежит в основе математической теории теплопроводности.

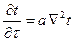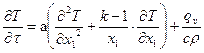; -диф.уравнение теплопроводности с источниками теплоты внутри тела.qv-количество выделяемой теплоты в единице объема вещества в единицу времени,вт/м^2,с-массовая теплоемкость,дж/(кг*град),р-плотность,кг/м^3

- Температуропроводность (коэффициент температуропроводности) — физическая величина, характеризующая скорость изменения (выравнивания) температуры вещества в неравновесных тепловых процессах. Численно равна отношению теплопроводности к объёмной теплоёмкости при постоянном давлении, в системе СИ измеряется в м²/с. 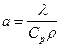где a— температуропроводность, — теплопроводность, Ср— изобарная удельная теплоёмкость,ρ— плотность

-Это дифференциальное уравнение носит название уравнения Пуассона. 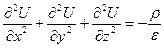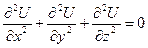-оператор Лапласса.

9.Краевые условия.

краевые условия задают начальное распределение температуры в заданной расчетной области и условия теплообмена на границе этой области.

Начальные Условия имеют вид: Т (х, 0) = Т₀ = const.

При граничных условиях I рода задают значение температуры на границе расчетной области.

При граничных условиях II рода задают значение плотности теплового потока на границе расчетной области.

При граничных условиях III рода задают температуру внешней среды, окружающей тело, и закон теплообмена между средой и поверхностью тела.

С учетом закона Фурье ГУ III рода можно записать следующим образом

,

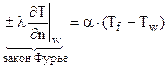где знак + или – в законе Фурье зависит от выбора начала системы координат.

В расчетах теплопроводности используют безразмерную форму записи граничных условий третьего рода: 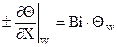, где 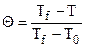– безразмерная температура; 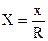– безразмерная координата, перпендикулярная поверхности теплообмена; R – характерный или определяющий размер тела; 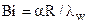– критерий Биó (Biot); λ_w – коэффициент теплопроводности твердого тела.

Граничные условия IV рода задают условия теплообмена на границе идеального контакта двух тел, состоящих из разного вещества с разными физическими свойствами

Date: 2015-05-05; view: 924; Нарушение авторских прав