
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Минимизация булевых функций. Карты Карно
|
|
Сложность логической функции, как уже было отмечено выше, определяется сложностью ее аналитической записи. Минимальной формой логической функции на некотором множестве фиксированных операций (базисе) можно считать такую, которая содержит минимальное число суперпозиций функций базиса, допуская и скобки. Однако построить эффективный алгоритм такой минимизации с получением минимальной скобочной формы трудно.
Более простой задачей минимизации является нахождение минимальная ДНФ функции. Для этой задачи существуют простые эффективные алгоритмы. Один из них основан на применении карт Карно.
Карта Карно – это двумерная табличная форма представления булевой функции, позволяющая в наглядной графической форме легко отыскать минимальные ДНФ логических функций. Каждой клетке в таблице сопоставляется дизъюнкт СДНФ минимизируемой функции, причем так, что любым осям симметрии таблицы соответствуют зоны, взаимно инверсные по какой-либо переменной. Такое расположение клеток в таблице позволяет легко определить склеивающиеся термы СДНФ (отличающиеся знаком инверсии только одной переменной): они располагаются в таблице симметрично. Например, следующая карта Карно построена для импликации двух переменных х ® у. В ячейки карты вписываются значения из таблицы истинности функции, при этом, если перед соответствующей переменной стоит знак отрицания, то в таблице истинности выбирается строка с ложным значением данной переменной, иначе – с истинным значением.
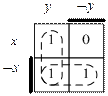
Все четыре клетки соответствуют всем возможным конъюнкциям СДНФ функции 2 переменных. Единичные значения функции показывают те дизъюнкты, которые присутствуют в СДНФ этой функции. Расположения элементов в картах Карно функции 2 переменных таково, что в один конъюнкт эта переменная входит без отрицания, а в другой – с отрицанием. Алгоритм поиска минимальной ДНФ по карте Карно основан на выявлении на карте минимального количества максимальных квадратов или прямоугольников со сторонами, равными степени двойки, так, чтобы они состояли только из ячеек, содержащих единицы. Для приведенной карты Карно единичные значения покрывают ячейки с координатами Ø х и у, соответственно искомая минимальная ДНФ будет Ø х Ú у.
Рассмотрим другую логическую функцию f = Ø p Ú q Å r Ù q Ù (p Ú r). Знаком Å обозначается операция сложения по модулю 2 или «исключающее или» (XOR – eXclusive OR), которая определяется следующим образом:
| х | у | х Å у |
| 0 | 0 | 0 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 0 |
Таблица истинности для данной формулы имеет следующий вид:
| p | q | r | f |
| 0 | 0 | 0 | 1 |
| 0 | 0 | 1 | 1 |
| 0 | 1 | 0 | 1 |
| 0 | 1 | 1 | 0 |
| 1 | 0 | 0 | 0 |
| 1 | 0 | 1 | 0 |
| 1 | 1 | 0 | 1 |
| 1 | 1 | 1 | 0 |
Карта Карно для функции трех переменных должна содержать, очевидно, 8 ячеек. Подобную карту можно изобразить следующим образом:
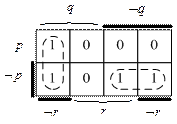
Для этой карты Карно единичные значения присутствуют в ячейках с координатами q Ù Ø r и Ø q Ù Ø p, соответственно минимальная ДНФ будет q Ù Ø r Ú Ø q Ù Ø p.
В силу симметрии карт Карно при построении прямоугольников возможно объединение ячеек, находящихся в крайних позициях, так как при ином расположении координат строк или столбцов (переменных без отрицания и с отрицанием) крайние ячейки окажутся внутри карты. Следующие две карты Карно эквивалентны (местами поменялись координаты r и Ø r) и на них указано корректное объединение ячеек в прямоугольные области:
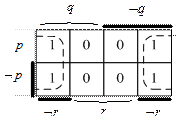
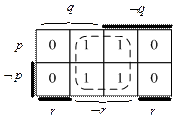
Карты Карно также удобны и для минимизации не полностью определенных функций. Например, пусть объявлена функция, у которой не определено часть значений:
| x | y | z | f |
| 0 | 0 | 0 | - |
| 0 | 0 | 1 | 1 |
| 0 | 1 | 0 | 1 |
| 0 | 1 | 1 | 1 |
| 1 | 0 | 0 | 0 |
| 1 | 0 | 1 | - |
| 1 | 1 | 0 | 1 |
| 1 | 1 | 1 | - |
При построении карты Карно для этой функции неопределенные значения можно заменить любыми – 0 или 1. Таким образом, выявляя на карте Карно прямоугольники из единиц, можно использовать ячейки, не содержащие значений.
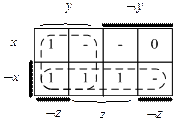
Для данного примера минимальная ДНФ равна y Ú Ø x.
Date: 2015-04-23; view: 855; Нарушение авторских прав