Понятие о приближённом числе. Абсолютная погрешность

1009. 1) Площадь океанов равна:

Тихого.............................. 179 679 тыс. кв. км

Атлантического................ 93 363 тыс. кв. км

Индийского...........................74 917 тыс. кв. км

Северного Ледовитого.......13 100 тыс. кв. км

Вычислить общую площадь этих океанов в миллионах квадратных километров, округлив данные в условии числа.

2) Округлить до тысяч следующие числа: 10 834 650; 4 354 160; 4 793 500; 6 381 480. Вычислить погрешность, допущенную при округлении.

3) Округлить до целых единиц следующие дробные числа: 228,7; 142,61; 374,4; 92,5; 93,5; 7 ²/₃; 4 ¹/₅. Вычислить погреш­ность, допущенную при округлении.

4) Округлить до десятых долей следующие дробные числа: 12,39; 87,15; 279,68; 156,44; 60,52; 3,25; 1,408. Вычислить по­грешность, допущенную при округлении.

1010. 1) Вычислить приближённые частные с точностью до целой единицы:

15 139:25; 78,66:0,13; 78,66:0,013.

2) Вычислить приближённые частные с точностью до 0,1: 14:3; 5,4:1,7; 15,4:4.

3) Вычислить приближённые частные с точностью до 0,01: 417:35; 17,51:6; 2,25:0,07; 39,5:1,3.

1011. Сколько квадратных километров площади приходится на одного жителя каждой из указанных частей света, если в Азии на 43 883 тыс. кв. км площади приходится 1 535 000 тыс. человек, в Африке на 30 284 тыс. кв. км площади приходится 224 000 тыс. человек, в Европе на 10498 тыс. кв. км площади приходится 569 000 тыс. человек. Вычисления произвести с точ­ностью до 0,01 кв. км.

1012. Древнегреческий учёный Архимед установил, что отношение длины окружности к её

до 0,01.

1013. Выразить приближённо десятичной дробью число 5 ²/₇ с тремя верными цифрами. Вычислить абсолютную погрешность полученного приближённого значения.

1014. Сравним время настенных и наручных часах. Пусть стенные часы показывают 2 часа 14 мин. (пополудни). Можно ли считать цифру 4 верной?

Пусть наручные часы в тот же момент показали 2 часа 13 мин. 15 сек. Можно ли считать цифру 5 верной? При решении задачи предпо­лагается, что и те и другие часы правильны.

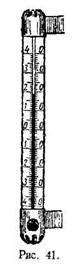
1015. 1) На наружном термометре столбик подкрашенного спирта находится между 18 и 19 делениями выше нуля (рис. 41). Ученик записал показания термомет­ ра числом 18,5°. Назовите верные цифры в этом числе. Как записать, что допущенная погрешность не превышает 0,5°?

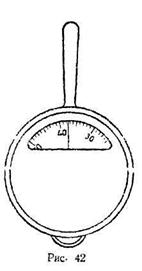
2) На рисунке 42 изображена шкала курвиметра. При обведе­нии части контура некоторой фигуры черта курвиметра оказалась между 37 и 38 делениями шкалы. Сколько сантиметров прошло колесо курвиметра, если каждое деление шкалы курвиметра со­ответствует 1 см длины? Ученик записал показание курвиметра 37,5 см. Назовите верные цифры в полученном числе. Как запи­сать, что допущенная погрешность не превышает 0,5 см?

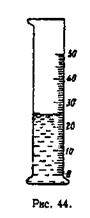
1016. На весах взвешено 150 г конфет. Рассмотрите рисунок части шкалы весов (рис. 43. стр. 172). Какой наименьший и наи­больший возможен вес данной покупки и какова наибольшая абсолютная погрешность при взвешивании на этих весах?

1017. 1) Ученик должен начертить план класса. Рулеткой он измерил длину а и ширину b и нашёл: а ≈ 8,50 м и b ≈ 6,20 м. Назовите верные цифры в полученных числах. Как записать, что возможная погрешность при измерении не превышает 5 см?

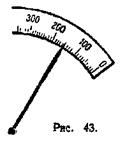
2) Измеряя мензуркой (рис. 44) объём жидкости, ученик полу­чил 26 куб. см. Назовите в полученном числе верные цифры. Ка­кую наибольшую погрешность мог допустить ученик при отсчёте на шкале мензурки?

1018. 1) Одна из старых русских мер длины — аршин (1 аршин ≈ 71,12 см) — выражала приближённо длину шага взрослого человека. Если принять 1 аршин приближённо за 71 см, то какова получится абсолютная погрешность? (Значение 71,12 см при решении задачи примите за точное выражение аршина в метрических мерах.)

2) Одна из старых русских мер веса — пуд при­ближённо равна 16,38 кг. Если принять, что 1 пуд≈16,4 кг, то чему равна абсолютная погрешность? (Число 16,38 кг при реше­нии задачи примите за точ­ное выражение пуда в метрических мерах.)

1019. Чтобы найти количество зёрен в 1 кг ржи, берут пять проб, по 10г каждую, и подсчитывают в каждой количество зёрен. Пусть при подсчётах получились числа: 308, 336, 327, 343 и 316. Подсчитайте среднее количество зёрен в 10 г ржи. Установите верные цифры полученного среднего значения. Для проверки верных цифр числа зёрен в 10 г ржи вычислите разность между значениями каждой пробы и найденным средним. Найдите среднее арифметическое этих разностей и по цифре стар­шего разряда его проверьте правильность взятых верных цифр в среднем значении числа зёрен в 10 г ржи. Чему считается равной в данном случае абсолютная погрешность результата? Сколько зерен содержится в 1 кг ржи?

1020. Ученик решил подсчитать число шагов, которое он де­лает на пути из дома в школу. Один раз он насчитал 950 шагов, другой — 938 и в третий — 965 шагов. Найдите среднее арифмети­ческое этих чисел. Вычислите разность между каждым значением слагаемых и средним. Найдите среднее арифметическое вычислен­ных разностей. Укажите верные цифры приближённого значения числа шагов.

Date: 2015-05-04; view: 1445; Нарушение авторских прав